Многомерное шкалирование (МШ)
Основное достоинство МШ – представление больших массивов данных о различии объектов в графическом виде. При МШ матрица различий между объектами (вычисленными, например, по их экспертным оценкам) представляется в виде одно-, двух– или трех– и более мерного графического изображения взаимного расположения этих объектов. Если две точки на изображении удалены друг от друга, то между соответствующими объектами имеется значительное расхождение; напротив, близость точек говорит о сходстве объектов. МШ имеет много общих черт с ФА. Так же, как и при ФА, создается система координат пространства, в котором определяется расположение точек. Так же, как и при ФА, происходит снижение размерности и упрощение данных. Однако при ФА обычно используются коэффициенты корреляции, а при МШ – меры различия между объектами. Наконец, в ФА наибольший интерес вызывают углы между точками, представляющими данные, а в МШ ключевой величиной является расстояние между этими точками. Помимо факторного анализа МШ имеет несколько общих черт с КА (см. раздел 3.5). В обоих случаях анализируется расстояние между объектами; однако при КА типичной является количественная процедура объединения объектов в группы (кластеры), а при МШ качественный анализ объектов проводится визуально с помощью диаграммы. Процедура ММШ SPSS, имеющая историческое название ALSCAL, фактически не является одной программой, а представляет собой набор небольших процедур, каждая из которых соответствует своему типу данных. В этом разделе будут приведены несколько примеров для различных типов данных. В первом примере будет обработана социограмма для группы учащихся; здесь их количественные оценки отношений друг к другу будут преобразованы в графическое изображение взаимного расположения учащихся. Во втором примере будут рассмотрены результаты тестирования учащихся по пяти показателям и графически представлены различия между учащимися на плоском изображении. Наконец, третий пример будет представлять собой небольшое исследование восприятия и понимания студентами пяти многомерных методов статистического анализа.
Вначале необходимо создать квадратную (12 × 12) матрицу различий. Позже на основе этой матрицы будет построено двухмерное изображение, иллюстрирующее взаимоотношения студентов. В ходе МШ исходная матрица 12 × 12 преобразуется в гораздо более простую матрицу 12 × 2 (где 2 – число измерений), содержащую координаты точек для изображения. Исходную матрицу называют квадратной асимметричной матрицей различий. Пояснения, что означают составляющие это определение термины, даны в конце настоящего раздела. 1. Откройте файл данных MDS-1.sav. В меню Analyze (анализ) выберите команду Scale ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). После выполнения предыдущего шага у Вас должно быть открыто диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные с1 – с12 в список Variables (переменные) (рис. 3.21).
3. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling: Model (многомерное шкалирование: модель). В группе Conditionality (условие) установите переключатель Row (строка) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.23).
5. Щелкните на кнопке ОК, чтобы открыть окно вывода.
´ Задача 3.9 [7]. Для решения требуется программа SPSS и файл данных MDS-2.sav. Квадратная симметричная матрица различий. Преподавателю необходимо рассадить 12 учащихся в соответствии с результатами их тестирования по пяти показателям. Поскольку результаты тестирования не относятся к данным, характеризующим различия, необходимо сначала вычислить различия по имеющимся данным и таким образом свести задачу к предыдущей. Исходные данные для этой задачи естественно представить в виде прямоугольной матрицы 12 × 5, в которой для каждого из 12 учащихся указаны результаты 5 тестов (файл MDS-2.sav). Затем по исходным данным строится квадратная (12 × 12) матрица различий между учащимися. Наконец, как и в предыдущем примере, SPSS создает матрицу координат 12 × 2 и визуально представляет ее в виде диаграммы. Обратите внимание на два ключевых свойства матрицы различий: она является квадратной и симметричной. Несмотря на то, что исходная матрица является прямоугольной, т. е. ее строки (объекты) соответствуют учащимся, а столбцы (переменные) – тестам, в матрице различий как строки, так и столбцы соответствуют учащимся, и, следовательно, матрица является квадратной с размером 12 × 12. Далее, поскольку, к примеру, учащийся 1 отличается от учащегося 5 по результатам тестирования так же, как учащийся 5 от учащегося 1, матрица различий является симметричной. В следующем примере демонстрируется двухмерное шкалирование квадратной симметричной матрицы различий, которую SPSS создает при задании переменных из файла данных. Данные матрицы различий имеют интервальный тип. В этом примере используется файл данных MDS-2.sav.
2. В группе Distances (расстояния) установите переключатель Create distances from data (вычислить расстояния по данным) и щелкните на кнопке Measure (мера), чтобы открыть диалоговое окно Multidimensional Scaling: Create Measure from Data (многомерное шкалирование: Создание меры для данных). В группе Create Distance Matrix (создание матрицы расстояний) установите переключатель Between cases (между объектами) и щелкните па кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.26).
3. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling: Model (многомерное шкалирование: модель). В группе Level of Measurement (уровень измерения) установите переключатель Interval (интервальный) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.27).
5. Щелкните на кнопке ОК, чтобы открыть окно вывода.
Шести студентам предложили сравнить между собой 5 многомерных статистических методов: множественный регрессионный анализ (МР), факторный анализ (ФА), кластерный анализ (КА), дискриминантный анализ (ДА) и многомерное шкалирование (МШ). Каждым студентом предъявляются все возможные пары из этих методов для оценки различия между ними (1 – максимально сходны,..., 5 – максимально различны). Затем по данным для 6 студентов составляется 6 матриц различий (5×5 каждая). Поскольку SPSS предъявляет определенные требования к формату данных при использовании модели индивидуальных различий, был создан специальный файл MDS-3.sav (рис. 3.28). Требования к формату файла сводятся к наличию в этом файле нескольких квадратных матриц одинакового размера. В файле MDS-3.sav присутствует 6 матриц размером 5×5. Первые 5 строк файла соответствуют первой матрице, следующие 5 строк – второй матрице, и т. д. Всего под матрицы отведено 30 строк. 1. Откройте файл данных MDS-3.sav. В меню Analyze (анализ) выберите команду Sca-le ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные mra – mds в список Variables (переменные) (рис. 3.21).
3. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling: Options (многомерное шкалирование: параметры). Установите флажок Croup plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24). 4. Щелкните на кнопке ОК, чтобы открыть окно вывода.
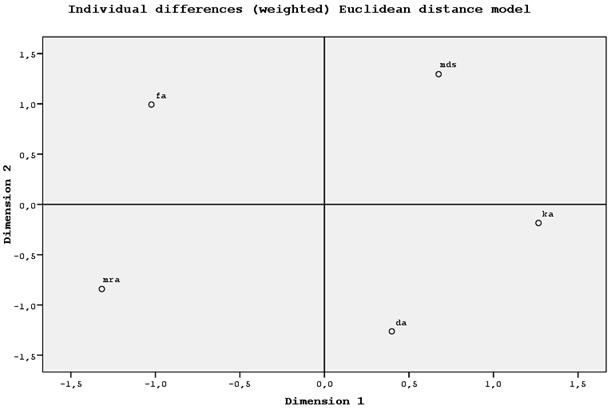
Dimension 1 (абсцисса) – слева расположены методы, основанные на корреляции, справа – на различиях по расстоянию. Dimension 2 (ордината) – сверху структурные методы, снизу – методы предсказания. Контрольные вопросы 1. Множественный регрессионный анализ (МР). 2. Факторный анализ (ФА). 3. Многомерное шкалирование (МШ). 4. Кластерный анализ (КА). 5. Дискриминантный анализ (ДА).
|

 ´ Задача 3.8 [7]. Для решения требуется программа SPSS и файл данных MDS-1.sav. Квадратная асимметричная матрица различий. Преподаватель решил создать идеальную психологическую обстановку в группе во время занятия, рассадив учащихся так, чтобы ни один из них не оказался рядом с тем, кто ему не нравится. Для этого каждому из 12 студентов было предложено оценить степень своей симпатии к своим однокурсникам по пятибалльной шкале (от 1 до 5, где 1 – максимум симпатии, а 5 – максимум антипатии). Результатом МШ будет диаграмма, на которой удаленность точек будет соответствовать отношениям между учащимися.
´ Задача 3.8 [7]. Для решения требуется программа SPSS и файл данных MDS-1.sav. Квадратная асимметричная матрица различий. Преподаватель решил создать идеальную психологическую обстановку в группе во время занятия, рассадив учащихся так, чтобы ни один из них не оказался рядом с тем, кто ему не нравится. Для этого каждому из 12 студентов было предложено оценить степень своей симпатии к своим однокурсникам по пятибалльной шкале (от 1 до 5, где 1 – максимум симпатии, а 5 – максимум антипатии). Результатом МШ будет диаграмма, на которой удаленность точек будет соответствовать отношениям между учащимися.
 2. Щелкните на кнопке Shape (форма), чтобы открыть диалоговое окно Multidimensional Scaling: Shape Of Data (многомерное шкалирование: форма данных). Установите переключатель Square asymmetric (квадратная асимметричная) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.22).
2. Щелкните на кнопке Shape (форма), чтобы открыть диалоговое окно Multidimensional Scaling: Shape Of Data (многомерное шкалирование: форма данных). Установите переключатель Square asymmetric (квадратная асимметричная) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.22). 4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling: Options (многомерное шкалирование: Параметры). Установите флажок Croup plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).
4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling: Options (многомерное шкалирование: Параметры). Установите флажок Croup plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).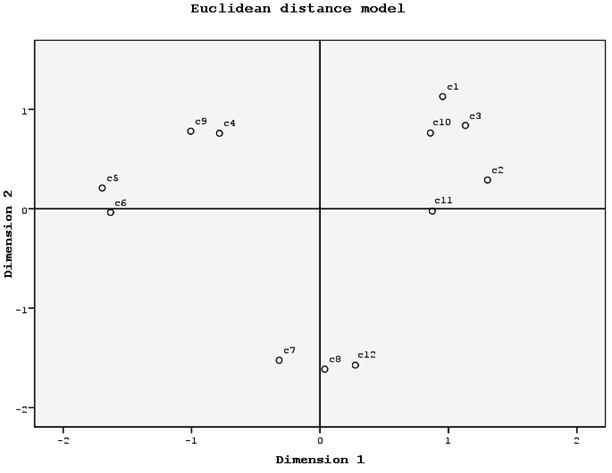

 1. Откройте файл MDS-2.sav. В меню Analyze (анализ) выберите команду Scale ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные тест1 – тест5 в список Variables (переменные) (рис. 3.25).
1. Откройте файл MDS-2.sav. В меню Analyze (анализ) выберите команду Scale ► Multidimensional Scaling (шкалирование ► многомерное шкалирование). Откроется диалоговое окно Multidimensional Scaling (многомерное шкалирование). Переместите переменные тест1 – тест5 в список Variables (переменные) (рис. 3.25). 4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling: Options (многомерное шкалирование: Параметры). Установите флажок Group plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).
4. Щелкните на кнопке Options (параметры), чтобы открыть диалоговое окно Multidimensional Scaling: Options (многомерное шкалирование: Параметры). Установите флажок Group plots (групповые диаграммы) и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование) (рис. 3.24).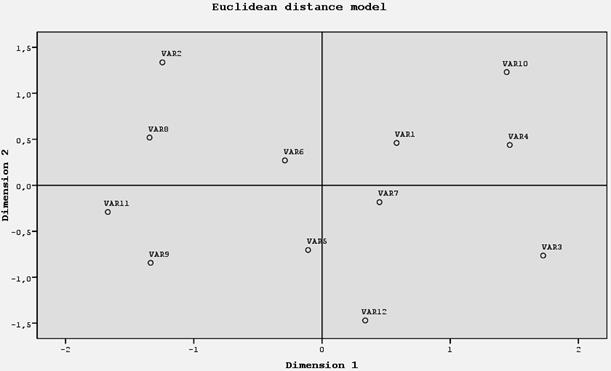
 ´ Задача 3.10 [7]. Для решения требуется программа SPSS и файл данных MDS-3.sav. Пример двухмерного шкалирования с использованием квадратных симметричных матриц и модели индивидуальных различий. В обоих рассмотренных примерах создавалась единственная матрица различий, на основе которой вычислялись координаты точек-объектов для визуального представления. Однако в некоторых случаях возможно координатное представление нескольких матриц различий; примером может служить ситуация, когда несколько экспертов оценивают один и тот же набор объектов. В этих случаях говорят о ММШ индивидуальных различий.
´ Задача 3.10 [7]. Для решения требуется программа SPSS и файл данных MDS-3.sav. Пример двухмерного шкалирования с использованием квадратных симметричных матриц и модели индивидуальных различий. В обоих рассмотренных примерах создавалась единственная матрица различий, на основе которой вычислялись координаты точек-объектов для визуального представления. Однако в некоторых случаях возможно координатное представление нескольких матриц различий; примером может служить ситуация, когда несколько экспертов оценивают один и тот же набор объектов. В этих случаях говорят о ММШ индивидуальных различий.
 2. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling: Model (многомерное шкалирование: модель), показанное на рис. 3.29. В группе Level of Measurement (уровень измерения) установите переключатель Ratio (отношение), а в группе Scaling Model (модель шкалирования) – переключатель Individual differences Euclidian distance (индивидуальные различия. Евклидово расстояние), после чего щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование).
2. Щелкните на кнопке Model (модель), чтобы открыть диалоговое окно Multidimensional Scaling: Model (многомерное шкалирование: модель), показанное на рис. 3.29. В группе Level of Measurement (уровень измерения) установите переключатель Ratio (отношение), а в группе Scaling Model (модель шкалирования) – переключатель Individual differences Euclidian distance (индивидуальные различия. Евклидово расстояние), после чего щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Multidimensional Scaling (многомерное шкалирование).


