Кластерный анализ (КА)КА имеет определенное сходство с ДА; сходство заключается в том, что исследователь в обоих случаях ставит перед собой цель разделить совокупность объектов (а не переменных) на несколько более мелких групп. Тем не менее, процесс классификации в двух видах анализа принципиально различен. В КА объекты классифицируются на основе их различия без какой-либо предварительной информации о количестве и составе классов. В ДА количество и состав классов изначально задан, и основная задача заключается в определении того, насколько точно можно предсказать принадлежность объектов к классам при помощи данного набора дискриминантных переменных (предикторов).
´ Задача 3.6. Для решения требуется программа SPSS и файл данных KA.sav, который содержит данные о 16 подержанных кардиотренажерах «беговая дорожка» разных марок, выставленных на продажу. Провести КА объектов.
2. В меню Analyze (анализ) выберите команду Classify ► Hierarchical Cluster (Классификация ► иерархическая кластеризация). Откроется диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ) (рис. 3.15). Переменную фирма переместите в поле Label Cases by (Различать объекты по), а переменные цена – усл_км переместите в список Variable(s) (переменные). 3. Щелкните на кнопке Plots (диаграммы), чтобы открыть диалоговое окно Hierarchical Cluster Analysis: Plots (иерархический кластерный анализ: диаграммы) (рис. 3.16). Установите флажок Dendrogram (дендрограмма) и переключатель None (нет) в группе Icicle (диаграмма накопления). Щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
5. Щелкните па кнопке Save (сохранить), чтобы открыть диалоговое окно Hierarchical Cluster Analysis: Save New Variables (иерархический кластерный анализ: сохранение новых переменных) (рис.3.18). Установите переключатель Single Solution (заданное число кластеров), введите в расположенное рядом поле значение 3 и щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ). 6. Щелкните па кнопке ОК, чтобы открыть окно вывода.
2. По умолчанию используется квадрат Евклидова расстояния, согласно которому расстояние между объектами равно сумме квадратов разностей между значениями одноименных переменных объектов. Предположим, что тренажер А имеет показатели технического состояния и эксплуатации 7 и 7, а тренажер В – 6 и 13. В этом случае расстояние между тренажерами вычисляется следующим образом: (7 – 6)2 + (7 – 13)2 = 37. При выполнении КА сумма квадратов разностей вычисляется для всех переменных. Получаемые расстояния используются программой при формировании кластеров. Помимо Евклидова существуют и другие виды расстояний. При необходимости обратитесь к руководству пользователя SPSS. Относительно вычисления расстояния может возникнуть следующий вопрос: будет ли адекватным результат КА в том случае, если переменные имеют различные шкалы измерения? Так, все переменные файла KA.sav имеют самые разные шкалы. Для решения проблемы шкалирования в SPSS используется стандартизация, в частности, ее простой метод – нормализация переменных, приводящая все переменные к стандартной z-шкале (среднее равно 0, стандартное отклонение – 1). Помимо одинаковой шкалы нормализованные переменные также имеют равные веса. В случае, если все исходные данные имеют одну и ту же шкалу измерения либо веса переменных по смыслу должны быть разными, стандартизацию переменных проводить не нужно. 3. Существует два основных метода формирования кластеров: метод слияния и метод дробления. В первом случае исходные кластеры увеличиваются путем объединения до тех пор, пока не будет сформирован единственный кластер, содержащий все данные. Метод дробления основан на обратной операции: сначала все данные объединяются в один кластер, который затем делится на части до тех пор, пока не будет достигнут желаемый результат. По умолчанию программой SPSS используется метод слияния, и мы рассмотрим его в этом разделе. В методе слияния предусмотрено несколько способов объединения объектов. Способ, применяемый по умолчанию, называется межгрупповым связыванием, или связыванием средних внутри групп. SPSS вычисляет наименьшее среднее значение расстояния между всеми парами групп и объединяет две группы, оказавшиеся наиболее близкими. На первом шаге, когда все кластеры представляют собой одиночные объекты, данная операция сводится к обычному попарному сравнению расстояний между объектами. Термин «среднее значение» приобретает смысл лишь на втором этапе, когда сформированы кластеры, содержащие более одного объекта. Так, в нашем примере на начальном этане имеется 16 кластеров (объектов); сначала в кластер объединяются два объекта с наименьшим расстоянием друг от друга. Затем подсчет расстояний повторяется, и в кластер объединяется еще одна пара переменных. На втором этапе вы получите либо 13 свободных объектов и 1 кластер, объединяющий 2 объекта, либо 11 свободных объектов и 2 кластера по 2 объекта в каждом. В конечном счете, все объекты окажутся в одном большом кластере. Существуют и другие методы объединения объектов. При необходимости обратитесь к руководству пользователя SPSS. 4. Как и в случае ФА, желаемое число кластеров и оценка результатов анализа зависят от целей исследователя. Для данного примера наиболее предпочтительно число кластеров, равное 3. Как показывает анализ, все тренажеры можно разделить на 3 группы: 1-я группа (на дендрограмме занимает центральное положение) имеет среднюю стоимость (среднее значение – 11883), небольшой срок эксплуатации (8 мес) и низкий условный километраж (3139 км). 2-я группа (на дендрограмме – вверху) имеет низкую стоимость (8750), небольшой пробег, наибольший возраст, не высокое техническое состояние (6). 3-я группа (на дендрограмме – внизу) содержит дорогие модели с небольшим сроком эксплуатации и изношенности, высоким баллом технического состояния.
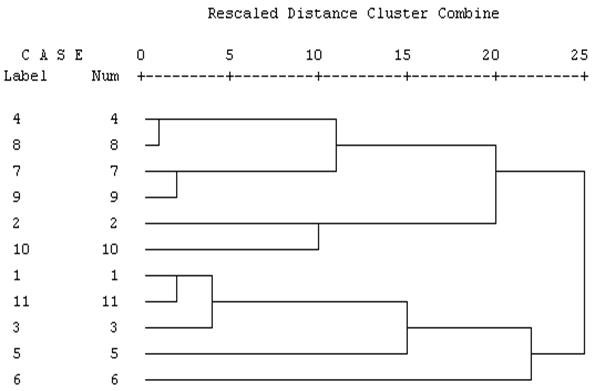
´ Задача 3.7 [7]. Для решения требуется программа SPSS и файл данных DA-FA-KA.sav. В этой задаче проводится КА, в котором вместо объектов участвуют переменные и1 – и11. Обычно при группировании переменных исследователя интересует их взаимосвязь, а не их различие (сходство), как при группировании объектов. Исключением является случай, когда данные представляют собой оценки объектов экспертами, в этом случае строки соответствуют экспертам, а столбцы – оцениваемым объектам. Поскольку в нашем примере интерес представляют именно взаимосвязи между переменными и мы хотим сравнить результаты с ФА, то в качестве меры близости целесообразно выбрать корреляцию. При этом корреляции надо учитывать по абсолютной величине, так как большие (по модулю) отрицательные их величины так же свидетельствуют о связи, как и большие положительные. Все это необходимо иметь в виду, если речь идет о кластеризации переменных. Большинство остальных параметров команды оставим установленными по умолчанию; даже в стандартизации в данном случае нет необходимости, так как на величину корреляции не влияют единицы измерения переменных. Добавим лишь дендрограмму в выводимые результаты и исключим оттуда диаграмму накопления. 1. Откройте файл данных DA-FA-KA.sav. 2. 3. Щелкните на кнопке Plots (диаграммы), чтобы открыть диалоговое окно Hierarchical Cluster Analysis: Plots (иерархический кластерный анализ: диаграммы) (рис. 3.16). Установите флажок Dendrogram (дендрограмма) и переключатель None (нет) в группе Icicle (диаграмма накопления). Щелкните на кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ). 4. 5. Щелкните на кнопке ОК, чтобы открыть окно вывода.
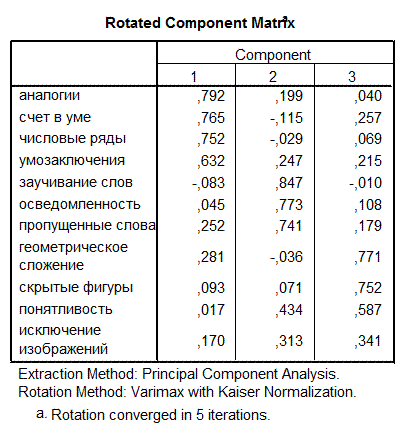
Сравните результаты КА и ФА, изображенные выше (см. файл DA-FA-KA.sav).
|
Выделяют несколько этапов КА: 1) выбор переменных-критериев для кластеризации; 2) выбор способа измерения расстояния между объектами, или кластерами (изначально считается, что каждый объект соответствует одному кластеру); 3) формирование кластеров; 4) интерпретация результатов.
1. Откройте файл данных KA.sav.
4. Щелкните на кнопке Method (метод), чтобы открыть диалоговое окно Hierarchical Cluster Analysis: Method (иерархический кластерный анализ: метод) (рис. 3.17). В списке Cluster Method (метод кластеризации) оставьте выбранным пункт Between–groups linkage (межгрупповое связывание), в списке Standardize (стандартизация) выберите пункт Z score (z-шкала) и щелкните па кнопке Continue (продолжить), чтобы вернуться в диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ).
Примечания: 1. В данном примере кластеризация осуществляется по следующим переменным: цена (стоимость), т_сост (экспертная оценка технического состояния по 10-балльной шкале), эксплуат (количество месяцев эксплуатации), усл_км (кол-во условных километров пробега с начала эксплуатации).
В меню Analyze (анализ) выберите команду Classify ► Hierarchical Cluster (классификация ► иерархическая кластеризация). Откроется диалоговое окно Hierarchical Cluster Analysis (иерархический кластерный анализ) (рис.3.19). В группе Cluster (кластеризация) установите переключатель Variables (переменные). Переместите переменные и1 – и11 в список Variable(s) (переменные).
