Пусть все функции 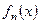 функциональной последовательности непрерывно-дифференцируемы на отрезке
функциональной последовательности непрерывно-дифференцируемы на отрезке  (т.е. имеют непрерывную производную), причем функциональный ряд составленный из производных
(т.е. имеют непрерывную производную), причем функциональный ряд составленный из производных 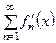 равномерно сходится на этом отрезке. Тогда сумма функционального ряда (3)
равномерно сходится на этом отрезке. Тогда сумма функционального ряда (3)  дифференцируема на
дифференцируема на  , причем выполняется:
, причем выполняется:
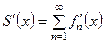 . (19)
. (19)
При этом говорят, что допустимо почленное дифференцирование функционального ряда.
Степенные ряды
Функциональный ряд вида
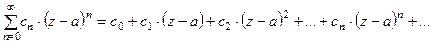 , (1)
, (1)
где 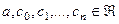 - фиксированные числа, а z – переменная называется степенным рядом с центром a и коэффициентами
- фиксированные числа, а z – переменная называется степенным рядом с центром a и коэффициентами 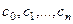 .
.
При 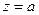 , ряд (1) сходится к единице при любых
, ряд (1) сходится к единице при любых 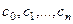 . Поэтому область сходимости степенного ряда не является пустым множеством.
. Поэтому область сходимости степенного ряда не является пустым множеством.
Линейной подстановкой  ряд (1) приводится к ряду
ряд (1) приводится к ряду
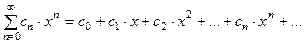 , (2)
, (2)
все свойства которого совпадают со свойствами ряда (1). Поэтому в дальнейшем будем рассматривать только степенные ряды с центром в точке 0.
Th 1. Теорема Абеля.
Пусть ряд (2) сходится в некоторой точке 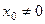 ,тогда ряд (2) сходится абсолютно в любой точке
,тогда ряд (2) сходится абсолютно в любой точке 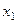 , удовлетворяющей условию
, удовлетворяющей условию 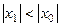 .
.
□
По условию числовой ряд 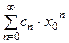 сходится, следовательно, выполняется необходимый признак сходимости
сходится, следовательно, выполняется необходимый признак сходимости 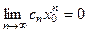 . Но тогда
. Но тогда
 ,
, 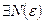 ,
, 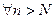
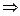
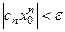 .
.
Отсюда
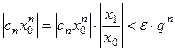 ,
, 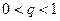 . А так как ряд
. А так как ряд 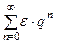 - сходящаяся геометрическая прогрессия, то ряд
- сходящаяся геометрическая прогрессия, то ряд  сходится по первому признаку сравнения, т.е. сходится абсолютно ряд
сходится по первому признаку сравнения, т.е. сходится абсолютно ряд 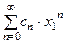 .
.
■

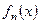 функциональной последовательности непрерывно-дифференцируемы на отрезке
функциональной последовательности непрерывно-дифференцируемы на отрезке  (т.е. имеют непрерывную производную), причем функциональный ряд составленный из производных
(т.е. имеют непрерывную производную), причем функциональный ряд составленный из производных 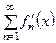 равномерно сходится на этом отрезке. Тогда сумма функционального ряда (3)
равномерно сходится на этом отрезке. Тогда сумма функционального ряда (3)  дифференцируема на
дифференцируема на 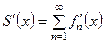 . (19)
. (19)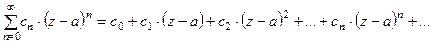 , (1)
, (1)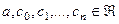 - фиксированные числа, а z – переменная называется степенным рядом с центром a и коэффициентами
- фиксированные числа, а z – переменная называется степенным рядом с центром a и коэффициентами 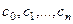 .
.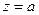 , ряд (1) сходится к единице при любых
, ряд (1) сходится к единице при любых  ряд (1) приводится к ряду
ряд (1) приводится к ряду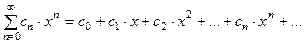 , (2)
, (2)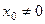 ,тогда ряд (2) сходится абсолютно в любой точке
,тогда ряд (2) сходится абсолютно в любой точке 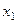 , удовлетворяющей условию
, удовлетворяющей условию 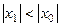 .
.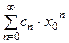 сходится, следовательно, выполняется необходимый признак сходимости
сходится, следовательно, выполняется необходимый признак сходимости 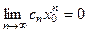 . Но тогда
. Но тогда ,
, 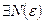 ,
, 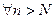
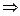
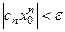 .
.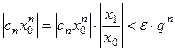 ,
, 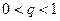 . А так как ряд
. А так как ряд 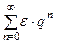 - сходящаяся геометрическая прогрессия, то ряд
- сходящаяся геометрическая прогрессия, то ряд  сходится по первому признаку сравнения, т.е. сходится абсолютно ряд
сходится по первому признаку сравнения, т.е. сходится абсолютно ряд 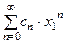 .
.


