Использование степенных рядов
Степенные ряды применяют при вычислении определенных интегралов. Для этого раскладывают подынтегральную функцию в степенной ряд и вычисляют полученный интеграл почленно. I
В тех случаях, когда не удается решить дифференциальное уравнение, его можно решить с помощью рядов. I Рассмотрим линейное дифференциальное уравнение второго порядка с переменными коэффициентами Предположим, что функция Подставим это разложение в дифференциальное уравнение Заменим в первой сумме Это уравнение преобразуется в тождество, если равны коэффициенты при одинаковых степенях x:
Из последнего равенства следует:
или
В результате точное общее решение уравнения имеет вид:
Приближенное частное решение задачи Коши можно определять другим способом: I Воспользуемся разложением решения в ряд Маклорена Найдем производные, подставляя в исходное уравнение начальные условия и дифференцируя его.
Получим приближенное решение
|
.
. Это уравнение не соответствует ни одному из трех типов дифференциальных уравнений, допускающих понижение порядка.
, являющаяся решением уравнения, разложена в степенной ряд 
. Тогда 
, 
.
.
, 
.
: 
, 
: 
, 
: 
,
: 
,... 
: 
.
, 
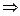
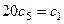и рекуррентное соотношение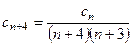 
, которое позволяет выразить остальные коэффициенты через 
, 
, 
, 
:
, 
, 
, 
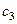, или
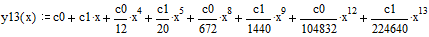
, если 
, 
.
.
, 
, 
, 
, 
,
,...
