Численные методы безусловной оптимизации нулевого порядка
Решение многих теоретических и практических задач сводится к отысканию экстремума (наибольшего или наименьшего значения) скалярной функции f(х) n -мерного векторного аргументах. В дальнейшем под x будем понимать вектор-столбец (точку в n -мерном пространстве):
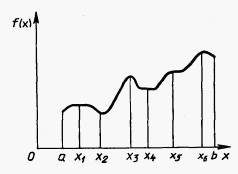
Вектор-строка получается путем применения операции транспонирования: Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности. В дальнейшем без ограничения общности будем говорить о поиске минимального значения функции f(x) записывать эту задачу следующим образом: f(x) --> min. Вектор х*, определяющий минимум целевой функции, называют оптимальным. Отметим, что задачу максимизации f(x) можно заменить эквивалентной ей задачей минимизации или наоборот. Рассмотрим это на примере функции одной переменной (Рис. 2.1). Если х * - точка минимума функции y = f(x), то для функции y =- f(x) она является точкой максимума, так как графики функций f(x) и - f(x), симметричны относительно оси абсцисс. Итак, минимум функции f(x) и максимум функции - f(x) достигаются при одном и том же значении переменной. Минимальное же значение функции f(x), (1-8-3/5) равно максимальному значению функции - f(x), взятому с противоположным знаком, т.е. min f(x) =-max (f(x)). Рассуждая аналогично, этот вывод нетрудно распространить на случай функции многих переменных. Если требуется заменить задачу минимизации функции f(x1, …, xn) задачей максимизации, то достаточно вместо отыскания минимума этой функции найти максимум функции f(x1, …, xn). Экстремальные значения этих функций достигаются при одних и тех же значениях переменных. Минимальное значение функции f(x1, …, xn) равно максимальному значению функции - f(x1, …, xn),взятому с обратным знаком, т.е. min f(x1, …, xn) =max f(x1, …, xn). Отмеченный факт позволяет в дальнейшем говорить только о задаче минимизации. В реальных условиях на переменные xj, i=1, …. n, и некоторые функции gi (х), hi(х), характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида: gi (х) = 0,i=1, …. n, hi (х) <= 0,i=1, …. n, a <= x <= b, где Такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации.
Точка х* определяет глобальный минимум функции одной переменной f(x), заданной на числовой прямой Х, если x * Точка х*
(1-8-4/5)
|

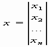
 .
. ;
; 
 Каждая точка х в n-мерном пространстве переменных х1, …, хn, в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой) называют допустимую точку х*, в которой целевая функция f (х) достигает своего минимального значения.
Каждая точка х в n-мерном пространстве переменных х1, …, хn, в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой) называют допустимую точку х*, в которой целевая функция f (х) достигает своего минимального значения. X и f(x*) < f(x) для всех x*
X и f(x*) < f(x) для всех x*