Построение пространственной модели стимулов
1. Определение базисной размерности. Определение достаточного числа измерений основано на выборе некоторого критерия, по которому оценивается расхождение между исходной матрицей данных и вычисленными межточечными расстояниями. В идеальном случае это расхождение должно равняться нулю, но в эмпирических данных всегда присутствуют случайные ошибки — шум, величина которого чаще всего неизвестна, поэтому на практике критерий выбирается не нулевой, но достаточно небольшой. Торгерсон предлагает следующий метод для определения минимальной размерности. Вычисляется центрированная матрица скалярных произведений между стимулами. Характеристические корни этой матрицы упорядочиваются по величине. Размерность определяется по числу собственных векторов, соответствующих наибольшим характеристическим корням, так, чтобы разброс полученных координат вносил достаточно большой вклад в дисперсию (75—96%). Остальная часть дисперсии рассматривается как следствие случайных ошибок. Метод определения минимального числа измерений в ходе построения пространственной модели впервые был предложен Шепардом. Он основан на общем принципе понижения размерности, который представляет собой растяжение больших и сжатие маленьких расстояний. Чтобы поместить треугольник в одномерном пространстве, не нарушая условия монотонности, необходимо сжать его меньшие стороны и растянуть большую. Процедура понижения размерности, так же как и достижение монотонности, основана на формировании множества векторов для каждой точки i, которые должны сжимать маленькие расстояния и растягивать большие. Критерием разделения расстояний на маленькие и большие служит среднее арифметическое расстояний. Поскольку процедура понижения размерности ориентирована на выполнение условия полной монотонности по отношению к различиям, то вместо рангов расстояний, которые на данном шаге итерации не обязательно удовлетворяют условию монотонности, лучше брать ранг самих различий. Тогда вектор, формирующийся для точки i по отношению к точке j, будет определять направление вектора (от точки i к точке j или наоборот), а величина разности (Dij - D) будет определять длину вектора. Сформированные таким образом (n-1) векторы для данной точки i также рассматриваются как действующие аналогично (n-1)-мерному вектору. Как и в ходе достижения монотонности, на каждом шаге итерации меняется положение всех n точек. При использовании подобных формальных критериев полезно учитывать, что качество аппроксимации исходных данных построенным пространством тем выше, чем больше выбранное число измерений. При увеличении размерности величина ошибки монотонно убывает (рис. 1), поэтому предпочтительнее такое число осей r, при котором эта функция становится достаточно пологой.
2. Вычисление координат. Метод ортогональных проекций. Если есть множество точек, заданных расстояниями между ними, то мы можем максимальное из этих расстояний принять за первую ось (Х1). Точки, заданные этим максимальным расстоянием, обозначим как 1 и 2, затем точку 1 на этой оси примем за начало оси Х1 и спроектируем ортогонально все остальные точки на ось Х1. Тогда точка 1 имеет координату Х11 = 0, а точка 2 — координату X12 = d12. Величина проекции для каждой точки i (кроме первых двух точек) вычисляется по известной геометрической формуле: Далее легко вычисляются расстояния от каждой точки до оси X1 по формуле:
Если все hi = 0, то очевидно, что все точки лежат на оси X1, т.е. (1-21-3/5) пространство данных точек одномерно. Если некоторые hi > 0, то из них выбирается максимальное (hmax) и принимается за ось Х2, то есть hmax = X23, а точка пересечения hmax с осью X1 есть начало оси X2 Затем все остальные точки ортогонально проецируются на ось Х2 и величина проекции вычисляется по формулам:
И в этом случае, если все qi = 0, то, следовательно, все точки лежат на плоскости Х1Х2 и выделение следующей оси пространства не имеет смысла.
Далее, если qi отличны он нуля, то выбирается точка с максимальным значением — qmax и принимается за четвертую точку, и тогда через эту точку 4 будет проходить ось Х3. Далее вычисляются проекции всех остальных точек на эту ось: Точка, наиболее удаленная от гиперплоскости в пространстве размерности r, ищется из условия: Процедура продолжается до тех пор, пока сумма всех проекций на k-ю ось не окажется меньше некоторого наперед заданного критерия. Например, эффективность решения можно определять отношением:
Число полученных осей рассматривается как минимальная размерность субъективного пространства, необходимая, чтобы удовлетворялась совместимость всех межточечных расстояний. Метод Торгерсона. Пусть dij, dik и djk — симметричные расстояния между тремя точками i, j и k. Рассмотрим симметричную матрицу Вi* с элементами b*ij и размерностью (n-1)(n-1), где: Элемент b*ij представляет собой скалярное произведение векторов от точки i к точкам j и k. Это
(1-21-4/5) легко показать с помощью закона косинуса, где для любых трех точек
Теоремы Янга и Хаусхольдера относятся к любой Вi* матрице: 1. Если матрица Вi* положительно полуопределена, расстояния между стимулами могут рассматриваться как расстояния между точками, лежащими в действительном евклидовом пространстве. В терминах характеристических корней или собственных значений матрицы Вi* это означает, что точки могут рассматриваться лежащими в действительном евклидовом пространстве, если все корни или положительны, или равны 0. Отрицательные характеристические корни предполагают мнимые пространства. 2. Ранг любой положительной полуопределенной матрицы равняется размерности множества точек. Количество положительных значений равняется числу осей, необходимых для описания взаимных межточечных расстояний. Для данного набора стимулов матрица Вi* будет иметь один и тот же ранг, независимо от того, какой стимул выбран как начало. 3. Любая положительная полуопределенная матрица Bi* может быть факторизована для получения матрицы X, где:
Алгоритм Янга-Торгерсона. На первом этапе исходная матрица различий анализируется метрическим методом Торгерсона. По числу наибольших характеристических корней определяется размерность пространства, и таким образом формируется исходная конфигурация для n точек, между которыми вычисляются n(n-1)/2 расстояний. На втором этапе данная конфигурация проверяется на выполнение условия монотонности. Для этого строится диаграмма монотонности. Она представляет собой график, осью абсцисс которого служат межточечные расстояния, а осью ординат — исходные различия. Каждой паре точек-стимулов (i,j) на этой диаграмме будет соответствовать точка с абсциссой dij и ординатой Dij. Условие монотонности означает, что от начальной точки графика каждая последующая точка должна располагаться только правее или выше предыдущей, и никогда не может быть ниже или левее. Если, следуя этому правилу, соединить последовательно все точки отрезками, то получится график, характеризующий монотонность связи между межточечными расстояниями и исходными различиями. Очевидно, что если для каких-либо пар точек-стимулов (i,j) монотонность не выполняется, то точки, представляющие их на диаграмме монотонности, не попадут на построенный график, а будут левее или ниже его. Для каждой выпавшей из графика точки можно вычислить ее отклонение от графика по оси абсцисс расстояний (по оси ординат это отклонение измерять не нужно, поскольку порядок различий задан как исходный) и сумма этих отклонений
|




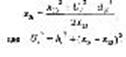 Объединив эти формулы, получим:
Объединив эти формулы, получим: Расстояние от каждой точки до плоскости Х1Х2 определится теперь как
Расстояние от каждой точки до плоскости Х1Х2 определится теперь как 


 Обычно ограничиваются таким количеством осей, которое дает разброс, исчерпывающий до 70-90% дисперсии.
Обычно ограничиваются таким количеством осей, которое дает разброс, исчерпывающий до 70-90% дисперсии.
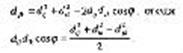 Из уравнений и следует, что b*ij = dijdikcosφ, т.е. скалярному произведению векторов из точки i к точкам j и k. Любая из n точек может быть взята как точка i. Таким образом существуют n матриц В*, из которых каждая может быть взята как данная матрица скалярных произведений.
Из уравнений и следует, что b*ij = dijdikcosφ, т.е. скалярному произведению векторов из точки i к точкам j и k. Любая из n точек может быть взята как точка i. Таким образом существуют n матриц В*, из которых каждая может быть взята как данная матрица скалярных произведений. Если ранг матрицы Вi* равен r, где r ≥ (n-1), тогда матрица X является прямоугольной матрицей (n-l) x r, элементы которой есть проекция точек на r-ортогональные оси с началом в i-ой точке r-мерного евклидова пространства. Допуская, что для выбора стимулов даны межточечные расстояния (не содержащие случайных ошибок), а матрица Вi* была построена в заданном начале, различные методики для факторизации матрицы Вi* дадут различные матрицы X, которые, однако, будут связаны ортогональным вращением осей. Матрицы Вi*, построенные посредством использования различных точек как начала расчета, дадут соответствующие матрицы X, которые не отличаются друг от друга с точностью до переноса и вращения осей.
Если ранг матрицы Вi* равен r, где r ≥ (n-1), тогда матрица X является прямоугольной матрицей (n-l) x r, элементы которой есть проекция точек на r-ортогональные оси с началом в i-ой точке r-мерного евклидова пространства. Допуская, что для выбора стимулов даны межточечные расстояния (не содержащие случайных ошибок), а матрица Вi* была построена в заданном начале, различные методики для факторизации матрицы Вi* дадут различные матрицы X, которые, однако, будут связаны ортогональным вращением осей. Матрицы Вi*, построенные посредством использования различных точек как начала расчета, дадут соответствующие матрицы X, которые не отличаются друг от друга с точностью до переноса и вращения осей.


