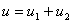Свободные колебания в поле постоянной силы.На материальную точку кроме упругой силы, действует сила постоянная по величине и направлению.
Рис.31
Обозначим ее
Начальные условия имеют вид: при Это неоднородное дифференциальное уравнение. Его решение складывается из решения однородного дифференциального уравнения и частного решения неоднородного дифференциального уравнения Решение имеет вид:
Если начало отсчета координаты сдвинуть на
Рис.32
Параллельное включение упругих элементов. Масса закреплена с помощью двух упругих элементов расположенных параллельно (рис.33).
Рис.33
Сместим массу на расстояние x.
Результирующая жесткость упругих элементов расположенных параллельно равна сумме жесткостей этих элементов.
Последовательное включение упругих элементов. Масса закреплена с помощью двух упругих элементов расположенных последовательно (рис.34).
Рис.34
Сместим массу на расстояние x. В упругих элементах возникает восстанавливающая (упругая) сила F, одинаковая для обоих элементов (рис.34). Первый упругий элемент изменит длину на x 1, второй - на x 2.
Обратная величина результирующей жесткости упругих элементов расположенных последовательно равна сумме обратных величин жесткостей этих элементов. Обратная величина жесткости упругого элемента называется податливостью этого элемента.
Результирующая податливость упругих элементов расположенных последовательно равна сумме податливостей этих элементов.
|
(рис.31), тогда дифференциальное уравнение движения точки примет вид:
или 
, где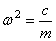 
: 
, 
.
.
,
, 
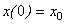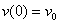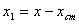(рис.32), тогда в новой системе отсчета решение будет иметь вид:
, 
- амплитуда колебаний;
, 
,
. 
, 
, 
.
, следовательно 
, 
, 
, 
