Свободные колебания без учета сил сопротивления.
Виділяють 4 групи продуктів: I — продукти енергетичні (хлібобулочні, макаронні, кондитерські вироби, крупи, цукор, картопля, жири і жирові продукти); II — продукти пластичного обліку (м’ясо, яйце, риба, молоко); III — продукти біорегуляторного пристосувального призначення (овочі, фрукти, ягоди, печінка тварин і риб, а також продукти для дієтичного харчування). IV — продукти сигнально-мотиваційного призначення (цибуля, часник, петрушка, тощо).
Якщо продукти будь-якої групи відсутні, то порушується обмін речовин. Набір продуктів у добовому раціоні з енергетичною цінністю 12 560 кДж (3000 ккал) становить: • 350 г хліба; • 40 г круп’яних виробів; • 5 г бобових; • 360 г картоплі; • 380—450 г овочів; • 200—220 г фруктів і ягід; • 190—210 г м’яса; • 50—55 гриби; • 0,5 л молока і кисломолочних продуктів; • 15 г сметани; • 20 г твердого сиру; • ЗО г м’якого сиру; • 2 яйця на 3 дні; • ЗО г вершкового масла; • 25 г рослинної олії. Їжа повинна мати приємний смак і аромат, відповідну консистенцію та температуру (не сильно гаряча і не холодна). їжа, подана до столу, повинна викликати бажання їсти. Добрий апетит залежить не тільки від органолептичних властивостей їжі та її оформлення, а й від різноманітності меню. Загальна кількість їжі на одне споживання не повинна обтяжувати роботу травної системи. Щоб запобігти зневодненню організму необхідно вживати достатню кількість рідини (чай, кава, кисіль, морси, компоти, соки, перші рідкі страви). Необхідно додержувати режиму харчування, ретельно пережовувати їжу, не поспішати. На сніданок і вечерю потрібно виділяти 30 хв, а на обід — 50 хв. Інтервали між споживаннями їжі не повинні бути надто довгими, але й короткі інтервали недоцільні. Тривалість інтервалів між споживанням їжі визначається індивідуально потребами кожної людини залежно від трудової діяльності та фізіологічних потреб організму.
Лекция 3. Прямолинейные колебания точки В данной лекции рассматриваются следующие вопросы: 1. Свободные колебания без учета сил сопротивления. 2. Понятие о фазовой плоскости. 3. Свободные колебания в поле постоянной силы. 4. Параллельное включение упругих элементов. 5. Последовательное включение упругих элементов. 6. Вынужденные колебания. Резонанс. 7. Свободные колебания с вязким сопротивлением. 8. Вынужденные колебания с вязким сопротивлением. Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин». Свободные колебания без учета сил сопротивления. Учение о колебаниях составляет основу ряда областей физики и техники. Хотя колебания, рассматриваемые в различных областях, например в механике, радиотехнике, акустике и др., отличаются друг от друга по своей физической природе, основные законы этих колебаний во всех случаях остаются одними и теми же. Поэтому изучение механических колебаний является важным не только по той причине, что такие колебания очень часто имеют место в технике, но и вследствие того, что результаты, полученные при изучении механических колебаний, могут быть использованы для изучения и уяснения колебательных явлений в других областях. Начнем с изучения свободных колебаний точки без учета сил сопротивления. Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы Fx=-cx.
Рис.27
Сила Найдем закон движения точки М. Составляя дифференциальное уравнение движения получим
Деля обе части равенства на т и вводя обозначение
приведем уравнение к виду
Уравнение представляет собою дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного однородного дифференциального уравнения второго порядка ищут в виде x=ent. Полагая x=ent, получим для определения п так называемое характеристическое уравнение, имеющее в данном случае вид п2 + k2 = 0. Поскольку корни этого характеристического уравнения являются чисто мнимыми (
где C 1 и С 2 - постоянные интегрирования. Если вместо постоянных C 1 и С 2 ввести постоянные а и Это другой вид решения, в котором постоянными интегрирования являются а и Скорость точки в рассматриваемом движении равна
Колебания, совершаемые точкой по закону Всем характеристикам этого движения можно дать наглядную кинематическую интерпретацию. Рассмотрим точку В, движущуюся равномерно по окружности радиуса а из положения В 0 определяемого углом Пусть постоянная угловая скорость вращения радиуса ОВ равна k. Тогда в произвольный момент времени t угол
Рис.28
Величина а, равная наибольшему отклонению точки М от центра колебаний, называется амплитудой колебаний. Величина Величина k, совпадающая с угловой скоростью вращения радиуса ОВ, показанного на рис.15 называется круговой частотой колебаний. Промежуток времени Т (или По истечении периода фаза изменяется на
Величина
Отсюда видно, что величина k отличается от Т только постоянным множителем Значения а и
Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k, а следовательно, и период Т колебаний от начальных условий не зависят.
Рис.29
Влияние постоянной силы на свободные колебания точки. Пусть на точку М, кроме восстанавливающей силы F, направленной к центру О, действует еще постоянная по модулю и направлению сила Р (рис.29). Величина силы F по прежнему пропорциональна расстоянию от центра О, т.е. Очевидно, что в этом случае положением равновесия точки М будет центр О 1 отстоящий от О на расстоянии
Величину
Отсюда заключаем, что постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силыF, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения
|

 , направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы
, направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы 
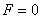 ; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.
; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента. .
. ,
, .
. ), то, как известно из теории дифференциальных уравнений, общее решение имеет вид
), то, как известно из теории дифференциальных уравнений, общее решение имеет вид ,
, , такие, что
, такие, что  ,
,  , то мы получим
, то мы получим  или
или  .
. .
. (рис.28).
(рис.28). и проекция М точки В на диаметр, перпендикулярный к DE, движется по закону
и проекция М точки В на диаметр, перпендикулярный к DE, движется по закону 
 называется фазой колебаний.
называется фазой колебаний. ), в течение которого точка совершает одно полное колебание, называется периодом колебаний.
), в течение которого точка совершает одно полное колебание, называется периодом колебаний. . Следовательно, должно
. Следовательно, должно  откуда период
откуда период .
. , обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний
, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний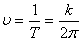 .
. ,
,  получим
получим  и
и  . Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:
. Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем: .
.

 , которое определяется равенством
, которое определяется равенством  или
или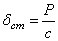 .
. назовем статическим отклонением точки. Примем центр O 1 за начало отсчета и направим координатную ось О 1 х в сторону действия силы
назовем статическим отклонением точки. Примем центр O 1 за начало отсчета и направим координатную ось О 1 х в сторону действия силы  . Тогда
. Тогда  ,
,  . В результате, составляя дифференциальное уравнение движения и учитывая, что согласно равенству
. В результате, составляя дифференциальное уравнение движения и учитывая, что согласно равенству  .
.


