Свободные колебания с вязким сопротивлением.Существуют устройства (демпферы), которые создают силу пропорциональную относительной скорости
Рис.36
Дифференциальное уравнение движения точки с массой m, закрепленной на упругом элементе и демпфере имеет вид:
Начальные условия имеют вид: Характеристическое уравнение имеет вид: Корни характеристического уравнения равны: Рассмотрим возможные решения: 1-й случай Решение имеет вид:
Рис.37
Материальная точка совершает гармонические колебания с частотой Движение изображающей точки на фазовой плоскости показано на рис. 38.
Рис.38
2-й случай Решение имеет вид:
Материальная точка совершает затухающее неколебательное движение (рис.39).
Рис.39
3-й случай Решение имеет вид:
Материальная точка так же совершает затухающее неколебательное движение (рис.39).
|
(рис.36). Коэффициент пропорциональности называется коэффициентом демпфирования или коэффициентом вязкого сопротивления.
или 
, 
, 
.
, 
, 
.
.
, 
, 
, 
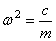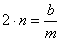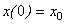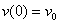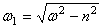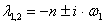
- условная амплитуда затухающих колебаний;
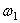- круговая или циклическая частота затухающих колебаний. Измеряется в рад/сек.
- фазовый угол (или просто фаза).
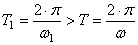- период затухающих колебаний (рис.37).
- частота колебаний (1 колеб/cек=1 Гц)
- декремент колебаний.
- логарифмический декремент колебаний.
, 
, 
, 
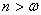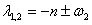
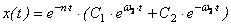
(два одинаковых корня)
