Рассмотрим важный случай колебаний, возникающих, когда на точку, кроме восстанавливающей силы  , действует еще периодически изменяющаяся со временем сила
, действует еще периодически изменяющаяся со временем сила  , проекция которой на ось Ох равна
, проекция которой на ось Ох равна
 .
.
Эта сила называется возмущающей силой, а колебания, происходящие при действии такой силы, называются вынужденными. Величина Р является частотой возмущающей силы.
Возмущающей силой может быть сила, изменяющаяся со временем и по другому закону. Мы ограничимся рассмотрением случая, когда  определяется указанным равенством. Такая возмущающая сила называется гармонической.
определяется указанным равенством. Такая возмущающая сила называется гармонической.
Рассмотрим движение точки, на которую, кроме восстанавливающей силы  , действует только возмущающая сила
, действует только возмущающая сила  . Дифференциальное уравнение движения в этом случае
. Дифференциальное уравнение движения в этом случае
 .
.
Разделим обе части этого уравнения на т и положим
 .
.
Тогда, учитывая обозначение, приведем уравнение движения к виду
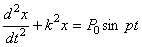 .
.
Уравнение является дифференциальным уравнением вынужденных колебаний точки при отсутствии сопротивления. Его решением, как известно из теории дифференциальных уравнений, будет  , где
, где 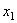 -общее решение уравнения без правой части, а
-общее решение уравнения без правой части, а 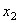 - какое-нибудь частное решение полного уравнения.
- какое-нибудь частное решение полного уравнения.
Полагая, что p = k, будем искать решение 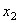 в виде
в виде
 ,
,
где А - постоянная величина, которую надо подобрать так, чтобы равенство обратилось в тождество. Подставляя значение 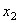 и его второй производной в уравнение будем иметь:
и его второй производной в уравнение будем иметь:
 .
.
Это равенство будет выполняться при любом t, если  или
или
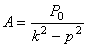 .
.
Таким образом, искомое частное решение будет
 .
.
Так как  , а общее решение имеет окончательно вид
, а общее решение имеет окончательно вид
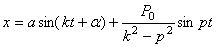 ,
,
где а и  - постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями
- постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями
Частота р вынужденных колебаний, как видно, равна частоте возмущающей силы. Амплитуду этих колебаний, если разделить числитель и знаменатель на  , можно представить в виде:
, можно представить в виде:
 ,
,
где  , т. е.
, т. е.  есть величина статического отклонения точки под действием силы
есть величина статического отклонения точки под действием силы  . Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний.
. Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний.
Подбирая различные соотношения между р и k, можно получить вынужденные колебания с разными амплитудами. При  амплитуда равна
амплитуда равна  (или близка к этой величине). Если величина р близка к k, амплитуда A становится очень большой. Когда
(или близка к этой величине). Если величина р близка к k, амплитуда A становится очень большой. Когда 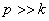 , амплитуда A становится очень малой (практически близка к нулю).
, амплитуда A становится очень малой (практически близка к нулю).
Резонанс. В случае, когда 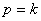 , т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.
, т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.

Рис.35

 , действует еще периодически изменяющаяся со временем сила
, действует еще периодически изменяющаяся со временем сила  , проекция которой на ось Ох равна
, проекция которой на ось Ох равна .
. определяется указанным равенством. Такая возмущающая сила называется гармонической.
определяется указанным равенством. Такая возмущающая сила называется гармонической. , действует только возмущающая сила
, действует только возмущающая сила  . Дифференциальное уравнение движения в этом случае
. Дифференциальное уравнение движения в этом случае .
. .
.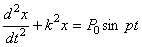 .
. , где
, где 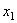 -общее решение уравнения без правой части, а
-общее решение уравнения без правой части, а 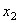 - какое-нибудь частное решение полного уравнения.
- какое-нибудь частное решение полного уравнения. ,
, .
. или
или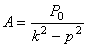 .
. .
.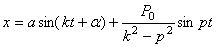 ,
, - постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями
- постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от начальных условий) и частотой k, называемых собственными колебаниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колебаниями , можно представить в виде:
, можно представить в виде: ,
, , т. е.
, т. е.  есть величина статического отклонения точки под действием силы
есть величина статического отклонения точки под действием силы  . Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний.
. Как видим, A зависит от отношения частоты р возмущающей силы к частоте k собственных колебаний. амплитуда равна
амплитуда равна 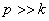 , амплитуда A становится очень малой (практически близка к нулю).
, амплитуда A становится очень малой (практически близка к нулю).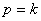 , т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.
, т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.



