Затылование по прямой
Фрезы, затылованные по спирали Архимеда, наряду с очевидными преимуществами, имеют серьезный недостаток: не позволяют сильно увеличивать главный задний угол Этих недостатков лишены фрезы, затылованные по прямой линии. Процесс затылования по прямой линии осуществляется при равномерном вращении фрезы и некоторым неравномерным прямолинейным перемещением затыловочного резца. При этом по прямой будет оформлен зуб на наружном диаметре фрезы, а другие участки профиля с Так как высота профиля зуба во всех радиальных сечениях должна быть постоянной, то боковой профиль зуба образуется кривыми, являющимися конхоидами прямой, описанными из полюса
Рис. 2.8. Прямая как кривая затылования Уравнение прямой линии
где Если от прямой Уравнение конхоиды прямой имеет вид
Пусть зуб фрезы располагается в системе координат так, чтобы главная задняя поверхность
Рис. 2.9. Задний угол при затыловании по прямой В точке Пусть точка
После определения производной выражения (2.19)
тогда
откуда
из треугольника
Из зависимости (2.22) видно, что с увеличением высоты профиля Если задний угол у самой нижней точки конхоиды В силу этого обстоятельства фрезы, затылованные по прямой, имеют малую высоту зуба и соответственно большее количество зубьев. Чтобы избежать большого числа зубьев у фрезы и обеспечить минимальную величину заднего угла по всей вершине зуба, применяют двойное затылование (мелкомодульные червячные фрезы, резьбофрезы). В этом случае максимальный задний угол берется для начальной точки
Рис. 2.10. Зуб фасонной фрезы с двойным затылком При подстановке в выражение
После элементарных алгебраических преобразований получается следующее выражение:
Если задаться углом Величина одинарного затылования по прямой линии (рис. 2.11, а) определяется по выражению
Из косоугольного треугольника
откуда следует
Для двойного затылования вывод формулы аналогичен (рис. 2. 11, б):
Рис. 2.11. Величина затылования: а - одинарное; б – двойное.
Из треугольника
откуда следует
Из треугольника
откуда следует
Подставив (2.28) в (2.27)
Из (2.25) и (2.29) получается
|

 , из-за чего боковые задние углы оказываются незначительными. По этой причине увеличивается износ боковых кромок, снижается стойкость фрезы, возрастает шероховатость обрабатываемой поверхности, снижается производительность из-за необходимости работы на пониженных режимах.
, из-за чего боковые задние углы оказываются незначительными. По этой причине увеличивается износ боковых кромок, снижается стойкость фрезы, возрастает шероховатость обрабатываемой поверхности, снижается производительность из-за необходимости работы на пониженных режимах. обтачиваются по некоторым вогнутым кривым.
обтачиваются по некоторым вогнутым кривым.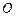 (рис. 2.8).
(рис. 2.8).
 в полярных координатах определяется из треугольника
в полярных координатах определяется из треугольника 
 (2.18)
(2.18) - радиус-вектор точки
- радиус-вектор точки  ;
; 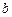 - расстояние от полюса до прямой
- расстояние от полюса до прямой 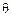 - полярный угол.
- полярный угол. вверх и вниз отложить высоту зуба
вверх и вниз отложить высоту зуба 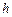 (на каждом луче из полюса
(на каждом луче из полюса  (2.19)
(2.19) (рис. 2.9).
(рис. 2.9).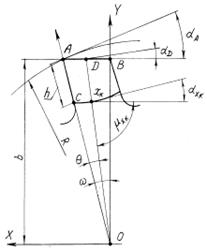
 задний угол
задний угол  имеет максимальное значение, а при переточках (например, плоскость
имеет максимальное значение, а при переточках (например, плоскость  ) уменьшается
) уменьшается  и в точке
и в точке  теоретически равен 0. Практически зуб стачивается на угол
теоретически равен 0. Практически зуб стачивается на угол  , поэтому в точке
, поэтому в точке 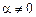 и имеет некоторое минимальное значение; эту величину можно задать и по ней найти центральный угол зуба
и имеет некоторое минимальное значение; эту величину можно задать и по ней найти центральный угол зуба 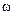 .
. , имеет координаты
, имеет координаты 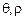 и находится на расстоянии
и находится на расстоянии  (2.20)
(2.20)

 . (2.21)
. (2.21) следует, что
следует, что 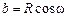 , а
, а  тогда
тогда (2.22)
(2.22)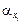 уменьшается (
уменьшается ( для точки
для точки  на вершине зуба или, если это возможно, уменьшить высоту профиля
на вершине зуба или, если это возможно, уменьшить высоту профиля 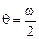 (рис. 2.10).
(рис. 2.10).
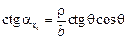 вместо
вместо 
 (2.23)
(2.23) .
. (2.24)
(2.24) по теореме синусов:
по теореме синусов:

 (2.25)
(2.25)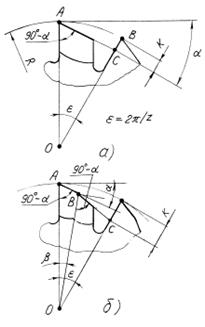
 (2.26)
(2.26) :
: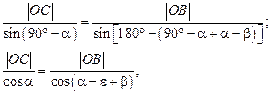
 (2.27)
(2.27)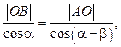
 (2.28)
(2.28) (2.29)
(2.29) (2.30)
(2.30)


