Сравнение кривых для затылования
Анализ рассмотренных выше кривых затылования показывает, что задние углы не остаются постоянными для всех точек профиля, а меняются в зависимости от удаленности от центра фрезы; кроме этого эти углы изменяются и при переточках фрезы. Логарифмическая спираль, хотя и обеспечивает постоянство заднего угла по верхней части зуба, на других участках профиля дает переменный задний угол и не имеет преимущества по сравнению со спиралью Архимеда. Непостоянство заднего угла в верхней части зуба, затылованного по спирали Архимеда, незначительно и на работу фрезы практически никакого влияния не оказывает. Кроме этого, задние углы в разных точках профиля (на конхоиде) у Архимедовой спирали изменяются более равномерно, чем у логарифмической спирали. Однако при выборе кривой затылования решающую роль играют технологические факторы. В настоящее время в практике, как в России, так и за рубежом применяется в качестве кривой затылования спираль Архимеда по следующим причинам: 1. Очень просто изготовить кулачок для затылования, так как у спирали Архимеда приращение радиус-вектора пропорционально приращению полярного угла Кулачок же с логарифмической спиралью изготавливается по разметке и последующей обработкой кривой по точкам. 2. Кулачок является универсальным, так как его можно использовать для фрез различных диаметров. Для логарифмической спирали и прямой линии для каждого диаметра фрезы требуется свой кулачок. Кулачки характеризуются величиной затылования В зависимости от условий резания устанавливается значение заднего угла При повороте фрезы на 1 угловой шаг В начальный момент (рис. 2.12, а) межцентровое расстояние равно
Когда фреза повернулась на Для положения 2.12, б:
Приравняв правые части выражений (2.31) и (2.32):
Рис. 2.12. Схема затылования В (2.33) величина
где Подставив (2.34) в (2.33):
Зависимость (2.35) есть уравнение спирали Архимеда, но для кулачка.
|

 ; кулачок легко изготовить на станке, у которого существует согласование между вращательным и поступательным движением.
; кулачок легко изготовить на станке, у которого существует согласование между вращательным и поступательным движением. , которая на практике выбирается в пределах
, которая на практике выбирается в пределах  мм в зависимости от размеров фрезы.
мм в зависимости от размеров фрезы. , затем по формуле
, затем по формуле 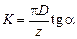 определяется величина затылования, и по ней подбирается кулачок. Иногда расчетное значение
определяется величина затылования, и по ней подбирается кулачок. Иногда расчетное значение  кулачок делает полный оборот:
кулачок делает полный оборот:  .
. (2.31)
(2.31)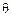 радиан (рис. 2.12, б), радиус-вектор точки пересечения затылка с линией центров стал равен
радиан (рис. 2.12, б), радиус-вектор точки пересечения затылка с линией центров стал равен  . Кулачок за это же время повернулся на угол
. Кулачок за это же время повернулся на угол  , радиус-вектор точки на спирали Архимеда кулачка стал равен
, радиус-вектор точки на спирали Архимеда кулачка стал равен  .
. (2.32)
(2.32) (2.33)
(2.33)
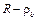 есть падение затылка зуба фрезы, полученное при повороте кулачка на угол
есть падение затылка зуба фрезы, полученное при повороте кулачка на угол  ; поэтому можно записать соотношение:
; поэтому можно записать соотношение: (2.34)
(2.34) – величина затылования зуба фрезы.
– величина затылования зуба фрезы. (2.35)
(2.35)


