Затылование по спирали Архимеда
Уравнение спирали Архимеда в полярных координатах (рис. 2.5) имеет вид:
где Угол
где
Рис. 2.5. Спираль Архимеда
тогда
Так как Из уравнения спирали Архимеда видно, что приращение радиус-вектора пропорционально приращению полярного угла. Поэтому вся поверхность зуба фрезы состоит из отрезков одной и той же спирали Архимеда, являющихся ее конхоидами (рис. 2.6).
Рис. 2.6. Задний угол на конхоиде спирали Архимеда Задний угол На глубине профиля
или Формула (2.15) показывает, что задние углы для разных точек профиля (для конхоиды спирали) есть переменные величины, увеличивающиеся с увеличением Из формулы
Подставив в формулу (2.15) вместо
Величина затылования определяется по аналогии с выводом формулы для затылования по логарифмической спирали (рис. 2.7).
Рис. 2.7. Величина затылования по архимедовой спирали Для точки 1 уравнение спирали Архимеда Величина затылования
|
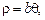(2.14)
- радиус-вектор точки на кривой; 
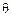- текущий полярный угол в радианах для точки на кривой; 
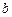- постоянный коэффициент, равный полярной поднормали; 
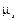между касательной и радиус-вектором для точки спирали Архимеда определяется по аналогии с предыдущим:
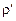- производная уравнения кривой по параметру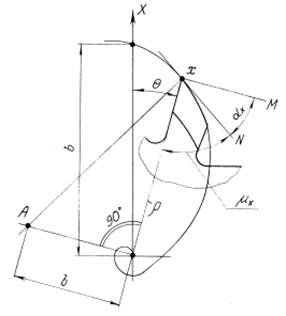 
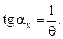
, а радиус-вектор есть переменная величина, то задний угол при переточках фрезы не является постоянным, а изменяется пропорционально полярному углу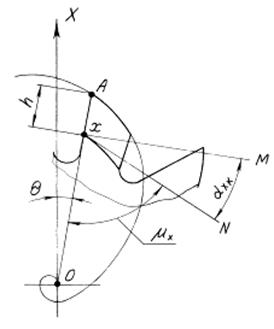 
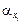определяется аналогично тому, как это делалось для логарифмической спирали.
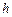имеется точка 
. Уравнение спирали Архимеда для нее: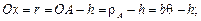
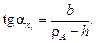(2.15)
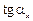и 
видно, что 
, так как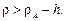 
следует
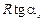, получится
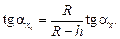(2.16)
. Для точки 2: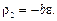 
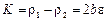. Известно, что 
, откуда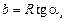 
. Тогда с учетом 
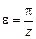получается
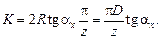(2.17)
