Пара множеств 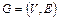 называется графом, если элементами множества
называется графом, если элементами множества 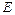 являются двухэлементные подмножества множества
являются двухэлементные подмножества множества  . Принято называть:
. Принято называть:  — множеством вершин или узлов,
— множеством вершин или узлов, 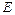 - множеством ребер графа
- множеством ребер графа 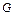 . Если
. Если  , то вершины
, то вершины 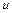 и
и 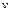 ,называют концами ребра
,называют концами ребра 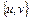 , которое соединяет их. На рисунках вершины изображают точками или кружками, ребра — отрезками прямых или кривых. На рис. 1.14. приведен граф
, которое соединяет их. На рисунках вершины изображают точками или кружками, ребра — отрезками прямых или кривых. На рис. 1.14. приведен граф 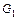 множеством вершин
множеством вершин 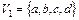 и множеством ребер
и множеством ребер 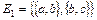 .
.

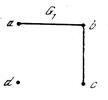
Рис. 1.14. Неориентированный граф 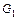 и его матрицы смежности и инцидентности
и его матрицы смежности и инцидентности
Матрицей смежности графа называется  матрица размера
матрица размера 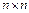 , содержащая в пересечении строки
, содержащая в пересечении строки 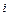 и столбца
и столбца 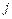 единицу, если
единицу, если  и ноль — в противном случае.
и ноль — в противном случае.
Ясно, что матрицы смежности графов симметричны относительно главной диагонали, поэтому в памяти компьютера их можно представлять верхним или нижним треугольником.
Матрицей инцидентности графа называется матрица размера  , содержащая в пересечении строки
, содержащая в пересечении строки 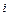 и столбца
и столбца 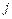 единицу, если
единицу, если 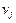 — конец ребра
— конец ребра 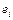 .
.
Граф называется двудольным, если множество его вершин разбивается на такие две доли, что концы любого ребра графа оказываются в разных долях. Граф 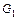 является двудольным с долями
является двудольным с долями 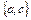 и
и  . Подмножество вершин графа называется независимым или внутренне устойчивым, если никакие две принадлежащие ему вершины не соединены ребром. Например, в графе
. Подмножество вершин графа называется независимым или внутренне устойчивым, если никакие две принадлежащие ему вершины не соединены ребром. Например, в графе 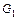 , независимыми множествами являются
, независимыми множествами являются  и
и  . Графы называют неориентированными, когда хотят отличить их от ориентированных.
. Графы называют неориентированными, когда хотят отличить их от ориентированных.
Пара множеств 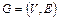 называется ориентированным графом, или короче — орграфом, если элементами множества
называется ориентированным графом, или короче — орграфом, если элементами множества 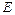 являются двучленные последовательности элементов множества
являются двучленные последовательности элементов множества  . Здесь
. Здесь  тоже называется множеством вершин или узлов, а
тоже называется множеством вершин или узлов, а 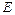 — множеством дуг или ориентированных ребер. Запись
— множеством дуг или ориентированных ребер. Запись  будем использовать для обозначения дуги и говорить, что она выходит из вершины
будем использовать для обозначения дуги и говорить, что она выходит из вершины 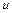 и входит в вершину
и входит в вершину 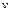 , или
, или 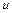 — начало,
— начало, 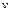 — конец дуги. На рисунках дуги изображают стрелками. На рис. 1.15 приведен орграф
— конец дуги. На рисунках дуги изображают стрелками. На рис. 1.15 приведен орграф 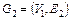 , где
, где  . Петлей называется дуга вида
. Петлей называется дуга вида  , но мы будем рассматривать орграфы без петель. Дуга
, но мы будем рассматривать орграфы без петель. Дуга 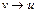 называется обратной по отношению к дуге
называется обратной по отношению к дуге  , а в паре их называют взаимно обратными.
, а в паре их называют взаимно обратными.
|
| A
| B
| C
| D
|

|
|
|
| -1
|

|
|
|
| -1
|
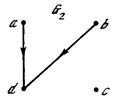
Рис. 1.15. Ориентированный граф 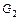 и его матрицы смежности и инцидентности
и его матрицы смежности и инцидентности
Соотнесенный орграф для неориентированного графа 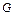 получается из
получается из 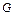 заменой каждого ребра парой взаимно обратных дуг, а соотнесенный неориентированный граф для орграфа
заменой каждого ребра парой взаимно обратных дуг, а соотнесенный неориентированный граф для орграфа 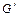 получается из
получается из 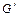 заменой каждой дуги и каждой пары взаимно обратных дуг на ребро. Если две вершины связаны ребром или дугой, то говорят, что эти ребро или дуга инцидентны им, а сами вершины называют смежными или соседями. Степенью вершины называется число инцидентных ей ребер или дуг. Вершина с нулевой степенью называется изолированной, с единичной — тупиковой. В орграфах число входящих в вершину (выходящих из вершины) дуг называется степенью входа (выхода}, а неизолированная вершина с нулевой степенью входа (выхода) называется истоком (стоком). В графе
заменой каждой дуги и каждой пары взаимно обратных дуг на ребро. Если две вершины связаны ребром или дугой, то говорят, что эти ребро или дуга инцидентны им, а сами вершины называют смежными или соседями. Степенью вершины называется число инцидентных ей ребер или дуг. Вершина с нулевой степенью называется изолированной, с единичной — тупиковой. В орграфах число входящих в вершину (выходящих из вершины) дуг называется степенью входа (выхода}, а неизолированная вершина с нулевой степенью входа (выхода) называется истоком (стоком). В графе 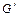 : вершины
: вершины  и
и 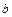 смежны,
смежны, 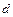 — изолированная,
— изолированная,  и
и 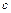 — тупиковые вершины. В орграфе
— тупиковые вершины. В орграфе  имеем: вершины
имеем: вершины  и
и 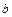 - истоки с единичной степенью выхода, вершина
- истоки с единичной степенью выхода, вершина  — сток со степенью входа два.
— сток со степенью входа два.
Далее будем использовать термин «граф», если неважно, о каком типе графа идет речь или если тип графа ясен из контекста. Хотя большинство следующих определений будет дано для неориентированных графов, все они, естественно, переносятся на орграфы. Особые пояснения для орграфов даются в скобках.

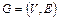 называется графом, если элементами множества
называется графом, если элементами множества 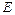 являются двухэлементные подмножества множества
являются двухэлементные подмножества множества  . Принято называть:
. Принято называть: 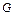 . Если
. Если  , то вершины
, то вершины 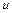 и
и 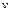 ,называют концами ребра
,называют концами ребра 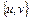 , которое соединяет их. На рисунках вершины изображают точками или кружками, ребра — отрезками прямых или кривых. На рис. 1.14. приведен граф
, которое соединяет их. На рисунках вершины изображают точками или кружками, ребра — отрезками прямых или кривых. На рис. 1.14. приведен граф 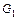 множеством вершин
множеством вершин 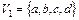 и множеством ребер
и множеством ребер 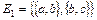 .
.

 матрица размера
матрица размера 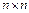 , содержащая в пересечении строки
, содержащая в пересечении строки 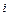 и столбца
и столбца 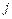 единицу, если
единицу, если  и ноль — в противном случае.
и ноль — в противном случае. , содержащая в пересечении строки
, содержащая в пересечении строки 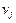 — конец ребра
— конец ребра 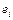 .
.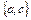 и
и  . Подмножество вершин графа называется независимым или внутренне устойчивым, если никакие две принадлежащие ему вершины не соединены ребром. Например, в графе
. Подмножество вершин графа называется независимым или внутренне устойчивым, если никакие две принадлежащие ему вершины не соединены ребром. Например, в графе  . Графы называют неориентированными, когда хотят отличить их от ориентированных.
. Графы называют неориентированными, когда хотят отличить их от ориентированных. будем использовать для обозначения дуги и говорить, что она выходит из вершины
будем использовать для обозначения дуги и говорить, что она выходит из вершины 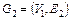 , где
, где  . Петлей называется дуга вида
. Петлей называется дуга вида  , но мы будем рассматривать орграфы без петель. Дуга
, но мы будем рассматривать орграфы без петель. Дуга 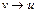 называется обратной по отношению к дуге
называется обратной по отношению к дуге 


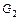 и его матрицы смежности и инцидентности
и его матрицы смежности и инцидентности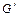 получается из
получается из  и
и 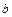 смежны,
смежны, 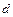 — изолированная,
— изолированная, 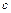 — тупиковые вершины. В орграфе
— тупиковые вершины. В орграфе  имеем: вершины
имеем: вершины 


