Определение огибающей семейства круговых проекций винтовой поверхности
Огибающей линией семейства кривых называется такая кривая, которая в каждой своей точке касается некоторой кривой из заданного семейства, представленное в виде массива точек и их координат. Каждая точка имеет обозначение номера кривой, которой она принадлежит, и номера своего расположения на данной кривой. На основе работ Панкратова Ю.М.[1] и Ступко В.Б.[2] предлагается методика определения огибающей. Суть методики заключается в том, что строятся отрезки прямых и дуги окружностей, которые касаются трех расположенных подряд кривых из семейства. По выбранным трем начальным точкам на трех соседних кривых строится дуга окружности и определяется центр окружности Для определения всех точек огибающей семейства кривых необходимо последовательно перебрать кривые и на каждой из них определить одну точку, которая принадлежит огибающей семейства (рис. 1.10). Для определения точки, принадлежащей огибающей, решается известная задача расчета координат центра окружности, проходящей через произвольно выбранные три точки на соседних трех кривых. При соединении трех точек отрезками получается треугольник, вписанный в окружность. Для определения координат текущего центра
Рис. 1.10. Расчетная схема определения огибающей линии семейства кривых
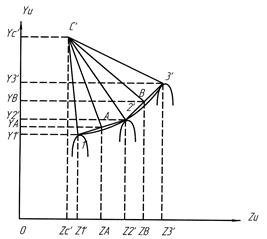
Рис. 1.11. Схема для определения координат центра окружности, проходящей через три точки Координаты центра Для решения задачи необходимо найти координаты точек
Коэффициенты угла наклона отрезков прямых
Учитывая выше приведенное условие, можно получить систему уравнений:
Преобразуя систему (1.21) с учетом (1.20) относительно
Приравняв два уравнения системы (1.22) и решив их относительно
Подставив полученное значение в первое уравнение системы (1.22), можно определить вторую координату центра Дальнейшим шагом является поиск точек на трех выбранных кривых, ближайших к точке Точка рассматриваемой кривой семейства, имеющая кратчайшее расстояние с текущим центром Математически описанное выше условие можно выразить следующим образом:
Тангенс угла наклона касательной определяется как первая производная к функции круговой проекции винтовых линий (1.19), которая имеет вид:
Рис. 1.12. Схема определения точки с кратчайшим расстоянием Выражение (1.25) можно записать через частные производные функции круговых проекций винтовых линий:
где
где
Подставив полученные частные производные (1.28) в систему (1.27), можно получить следующую систему уравнений:
Подставив (1.29) в (1.19), получится значение тангенса угла наклона касательной:
Котангенс угла наклона прямой, содержащей отрезок, соединяющий искомую точку на круговой проекции винтовой линии и рассматриваемый центр, определяется по следующей формуле:
Приравнивание выражения (1.31) и (1.30) дает уравнение, которое необходимо решить относительно параметра Если расстояние меньше значения величины
|

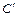 , а также и кратчайшее расстояние из этого центра до каждой из этих трех кривых. По найденным точкам
, а также и кратчайшее расстояние из этого центра до каждой из этих трех кривых. По найденным точкам 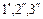 определяется центр
определяется центр 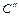 проходящей через них окружности, и процесс повторяется до тех пор, пока расстояние
проходящей через них окружности, и процесс повторяется до тех пор, пока расстояние 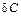 между положениями центров не окажется меньше величины наперед заданной точности
между положениями центров не окажется меньше величины наперед заданной точности 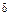 . Средняя точка
. Средняя точка 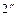 принимается за точку, принадлежащей огибающей семейства, и процедура повторяется со смещением на одну кривую.
принимается за точку, принадлежащей огибающей семейства, и процедура повторяется со смещением на одну кривую.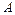 - середина отрезка
- середина отрезка 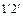 и
и  - середина отрезка
- середина отрезка  (рис. 1.11).
(рис. 1.11).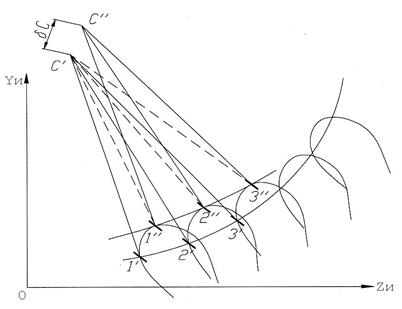
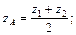
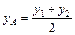 ;
; 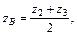
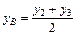 .
.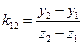 ;
; 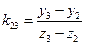 ;
; 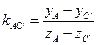 , (1.20)
, (1.20)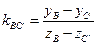 .
.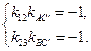 (1.21)
(1.21)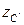 , можно получить систему вида:
, можно получить систему вида: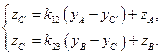 (1.22)
(1.22)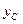 , получится формула вида:
, получится формула вида: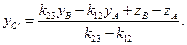 (1.23)
(1.23)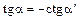 . (1.24)
. (1.24)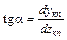 . (1.25)
. (1.25)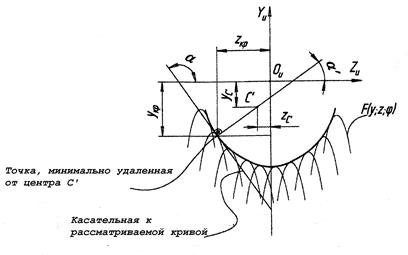
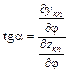 , (1.26)
, (1.26)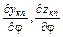 - частные производные по винтовому углу
- частные производные по винтовому углу  системы уравнений круговых проекций винтовых линий изделия (1.19):
системы уравнений круговых проекций винтовых линий изделия (1.19):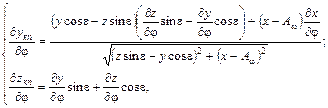 (1.27)
(1.27)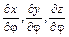 - частные производные уравнений, задающих винтовую поверхность изделия.
- частные производные уравнений, задающих винтовую поверхность изделия.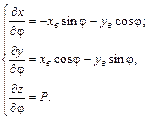 (1.28)
(1.28)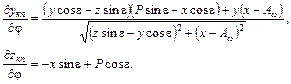 (1.29)
(1.29)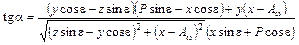 . (1.30)
. (1.30)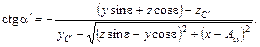 (1.31)
(1.31) с учетом диапазона изменения данного параметра, полученного в формуле (1.16). Для решения данного уравнения применяется хорошо известный метод половинного деления, после чего определяются координаты центра
с учетом диапазона изменения данного параметра, полученного в формуле (1.16). Для решения данного уравнения применяется хорошо известный метод половинного деления, после чего определяются координаты центра 


