Метод общих касательных
В основе метода общих касательных лежит тот же геометрический принцип, что и в методе общих нормалей. В точке контакта винтовой поверхности изделия и производящей поверхности вращения касательная к винтовой поверхности должна совпадать с касательной к поверхности вращения. Винтовая поверхность детали образуется винтовым движением отрезка
где Начало инструментальной системы координат В системе координат режущего инструмента уравнение винтовой поверхности изделия принимает вид
где
Рис. 1.4. Расчетная схема метода общих касательных Линия касания исходной инструментальной поверхности и винтовой поверхности детали определяется решением уравнения:
где При задании положения расчетных точек на профиле винтовой поверхности изделия
где угол
Уравнение является нелинейным и решается с применением средств компьютерной математики.
|
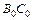и описывается уравнением в неподвижной системе координат 
.
(1.12)
- угол поворота отрезка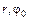 
- параметры, определяющие положение точки на отрезке 
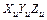- точка 
совпадает с точкой скрещивания осей вращения инструмента и заготовки 
. Ось 
направлена по кратчайшему расстоянию между осями инструмента 
и заготовки 
. Ось 
перпендикулярна координатной плоскости 
(рис. 1.4).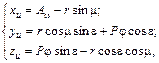
(1.13)
; 
- угол между осью 
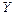и координатной плоскостью 
в плоскости 
.
(1.14)
- угол между направлением радиуса r и нормалью к отрезку 
по приведенному выше уравнению, после чего можно определить координаты профилирующей точки режущего инструмента
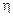определяется по формуле
