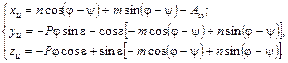Геометрической сутью метода общих нормалей является поиск общих нормалей в точках характеристики, которые всегда пересекают ось режущего инструмента, так как он представляет собой тело вращения.
Согласно обобщению теоремы Виллиса для технологической пары «исходная инструментальная поверхность вращения - винтовая поверхность детали» существует полюсная ось профилирования, роль которой аналогична роли полюса для плоского зацепления: нормали в точках характеристики проходят через полюсную ось профилирования  (рис. 1.3).
(рис. 1.3).
Положение  относительно оси детали, определяется расстоянием
относительно оси детали, определяется расстоянием  и углом
и углом  между ними из соотношения:
между ними из соотношения:
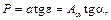
где 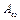 - межосевое расстояние, мм;
- межосевое расстояние, мм;  - угол скрещивания, рад;
- угол скрещивания, рад; 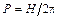 ,
,  - винтовой параметр, мм;
- винтовой параметр, мм;  - шаг винтовой линии, мм.
- шаг винтовой линии, мм.
Винтовая проекция оси  на торцовую плоскость
на торцовую плоскость 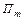 , проходящая через общий перпендикуляр к осям инструмента и винтовой поверхности, является центроидой детали
, проходящая через общий перпендикуляр к осям инструмента и винтовой поверхности, является центроидой детали  . Она находится как след, который оставляет на этой плоскости ось
. Она находится как след, который оставляет на этой плоскости ось  при ее винтовом перемещении с параметром
при ее винтовом перемещении с параметром  относительно оси детали.
относительно оси детали.
Поверхность детали задается параметром  и обобщенными координатами точек профиля в торцовом сечении,
и обобщенными координатами точек профиля в торцовом сечении,  где для каждой точки
где для каждой точки  :
:  - расстояние от касательной к поверхности детали до ее оси;
- расстояние от касательной к поверхности детали до ее оси;  - расстояние от нормали
- расстояние от нормали  к винтовой поверхности до оси детали;
к винтовой поверхности до оси детали;  - угол между положительным направлением оси
- угол между положительным направлением оси  и касательной к профилю.
и касательной к профилю.
Знаки этих координат принимаются следующим образом. При обходе профиля в направлении от точки 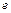 к точке
к точке  вектор касательной направлен навстречу обходу. При этом
вектор касательной направлен навстречу обходу. При этом  если центр
если центр  детали находится справа от касательной, и
детали находится справа от касательной, и  если центр
если центр  располагается выше
располагается выше  .
.

Рис. 1.3. Схема метода общих нормалей
Нормаль  в винтовом движении относительно оси обрабатываемой заготовки воспроизводит поверхность, которая в правой системе координат
в винтовом движении относительно оси обрабатываемой заготовки воспроизводит поверхность, которая в правой системе координат 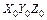 записывается системой уравнений:
записывается системой уравнений:
 (1.9)
(1.9)
где  - координата текущей точки нормали
- координата текущей точки нормали  в ее исходном положении по оси
в ее исходном положении по оси  ;
;  - независимый угловой параметр;
- независимый угловой параметр;  - угол скрещивания нормали с осью детали,
- угол скрещивания нормали с осью детали, 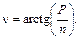
Из совместного решения уравнений винтовой проекции нормали, вытекающих из уравнений (1.9) при условии, что 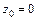 и уравнений центроиды, получающихся аналогичным путем, следует уравнение для нахождения точки искомой характеристики:
и уравнений центроиды, получающихся аналогичным путем, следует уравнение для нахождения точки искомой характеристики:
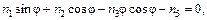 (1.10)
(1.10)
где 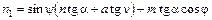 ;
;
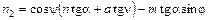 ;
;
 ;
;
 ,
,
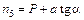 .
.
Полученное уравнение является трансцендентным. Для его решения необходимо применение численных методов. Решение уравнения (1.10) дает формулу для расчета значений его корней
 .(1.11)
.(1.11)
Для использования формулы (1.11) необходимо знать первое приближенное значение угла  , выбор которого целесообразно проводить на основе использования мгновенной центроиды обработки детали. Последняя получается при разложении винтового движения оси
, выбор которого целесообразно проводить на основе использования мгновенной центроиды обработки детали. Последняя получается при разложении винтового движения оси  на два составляющих движения, одно из которых – прямолинейное движение вдоль оси
на два составляющих движения, одно из которых – прямолинейное движение вдоль оси  , а другое - вращательное вокруг оси
, а другое - вращательное вокруг оси  , параллельной оси обрабатываемой заготовки и отстоящей от нее на расстоянии
, параллельной оси обрабатываемой заготовки и отстоящей от нее на расстоянии 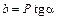 . Прямолинейное движение оси
. Прямолинейное движение оси  само по себе не меняет положения ее в пространстве, и его можно не принимать во внимание. Поэтому остается только вращательное движение вокруг оси
само по себе не меняет положения ее в пространстве, и его можно не принимать во внимание. Поэтому остается только вращательное движение вокруг оси  . Если принять положение оси
. Если принять положение оси  постоянным, то возникает погрешность определения угла
постоянным, то возникает погрешность определения угла  , что вполне возможно, так как на первом этапе требуется приближенное значение угла.
, что вполне возможно, так как на первом этапе требуется приближенное значение угла.
Координаты точек, принадлежащих профилю образующей исходной инструментальной поверхности, определяют с помощью системы уравнений:
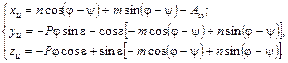

 (рис. 1.3).
(рис. 1.3). и углом
и углом  между ними из соотношения:
между ними из соотношения: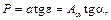
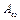 - межосевое расстояние, мм;
- межосевое расстояние, мм;  - угол скрещивания, рад;
- угол скрещивания, рад; 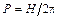 ,
,  - винтовой параметр, мм;
- винтовой параметр, мм;  - шаг винтовой линии, мм.
- шаг винтовой линии, мм.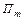 , проходящая через общий перпендикуляр к осям инструмента и винтовой поверхности, является центроидой детали
, проходящая через общий перпендикуляр к осям инструмента и винтовой поверхности, является центроидой детали  . Она находится как след, который оставляет на этой плоскости ось
. Она находится как след, который оставляет на этой плоскости ось  где для каждой точки
где для каждой точки  :
:  - расстояние от касательной к поверхности детали до ее оси;
- расстояние от касательной к поверхности детали до ее оси;  - расстояние от нормали
- расстояние от нормали  к винтовой поверхности до оси детали;
к винтовой поверхности до оси детали;  - угол между положительным направлением оси
- угол между положительным направлением оси  и касательной к профилю.
и касательной к профилю.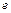 к точке
к точке  вектор касательной направлен навстречу обходу. При этом
вектор касательной направлен навстречу обходу. При этом  если центр
если центр  детали находится справа от касательной, и
детали находится справа от касательной, и  если центр
если центр 
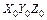 записывается системой уравнений:
записывается системой уравнений: (1.9)
(1.9)  - координата текущей точки нормали
- координата текущей точки нормали  ;
;  - независимый угловой параметр;
- независимый угловой параметр;  - угол скрещивания нормали с осью детали,
- угол скрещивания нормали с осью детали, 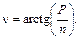
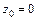 и уравнений центроиды, получающихся аналогичным путем, следует уравнение для нахождения точки искомой характеристики:
и уравнений центроиды, получающихся аналогичным путем, следует уравнение для нахождения точки искомой характеристики: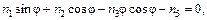 (1.10)
(1.10) 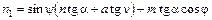 ;
;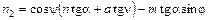 ;
; ;
; ,
,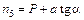 .
. .(1.11)
.(1.11)  , выбор которого целесообразно проводить на основе использования мгновенной центроиды обработки детали. Последняя получается при разложении винтового движения оси
, выбор которого целесообразно проводить на основе использования мгновенной центроиды обработки детали. Последняя получается при разложении винтового движения оси  , параллельной оси обрабатываемой заготовки и отстоящей от нее на расстоянии
, параллельной оси обрабатываемой заготовки и отстоящей от нее на расстоянии 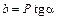 . Прямолинейное движение оси
. Прямолинейное движение оси