Определение кривой профиля червячной фрезы
Профиль фрезы представляет огибающую семейства профиля изделия при качении без скольжения его начальной окружности по начальной прямой фрезы. Поэтому задача сводится к определению уравнения семейства профиля изделия и уравнения их огибающей. Принимаются две декартовы системы координат: подвижная система координат Ось ОХ расположена по начальной прямой (рис. 1.1); начало неподвижной системы координат в начальный момент совпадает с полюсом зацепления, а на оси ОУ лежит центр начальной окружности.
Рис. 1.1. Аналитическое определение профиля фрезы как огибающей профиля изделия Профиль зуба фрезы определяется в неподвижной системе координат. В подвижной системе определяется профиль шлицевого валика. При перекатывании начальной окружности по начальной прямой без скольжения на угол Уравнение линии
Формулы перехода от подвижной системы координат к неподвижной имеют вид системы уравнений:
где При повороте детали начало координат подвижной системы перемещается по циклоиде, система уравнений которой, имеет вид:
Подставив в уравнение (1.2) значения
Переменив знаки, приведя к общему знаменателю и разделив на
Для определения огибающей полученного семейства профилей детали необходимо продифференцировать выражение (1.4) в частных производных по параметру φ и приравнять ее к нулю:
Подставив выражение (1.6) в уравнение семейства (1.5), можно найти:
Итак, система уравнений профиля червячной фрезы как огибающей семейства профилей изделия имеет вид:
Примечания: 1. В формулах (1.8) при расчете профиля фрезы углы брать в радианах. 2. Расчет необходимо производить с точностью до шестого знака; тригонометрические функции вычислять с точностью до угловых секунд. Полученные уравнения (1.8) в параметрической форме дают координаты точек огибающей семейства, т.е. координаты профиля фрезы. Давая различные значения углам φ, получим несколько точек искомой кривой, по которым строится профиль инструмента. После определения профиля фрезы для упрощения технологии изготовления фрез производят замену теоретического профиля дугами одной или двух окружностей, находя центр заменяющей окружности и ее радиус. При этом учитывается, что сумма положительных и отрицательных отклонений не должна превышать 2/3 допуска δ на прямолинейность профиля валика:
Рис. 1.2. Замена теоретического профиля дугой окружности
|

 и неподвижная
и неподвижная  . В начальный момент времени обе системы координат совпадают.
. В начальный момент времени обе системы координат совпадают.
 линия профиля
линия профиля  займет положение
займет положение  (уже в подвижной системе координат
(уже в подвижной системе координат  ).
). или
или  (1.2)
(1.2) (1.3)
(1.3)  и
и  - координаты центра подвижной системы координат
- координаты центра подвижной системы координат  в неподвижной системе
в неподвижной системе  ;
;  и
и  - координаты точки профиля в подвижной системе координта;
- координаты точки профиля в подвижной системе координта;  и
и 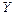 - координаты точки профиля в неподвижной системе координат.
- координаты точки профиля в неподвижной системе координат.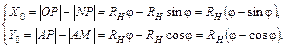 (1.4)
(1.4) и
и  из (1.3) и (1.4) и выполнив математические преобразования можно получить уравнение:
из (1.3) и (1.4) и выполнив математические преобразования можно получить уравнение:
 можно получить уравнение семейства профилей детали:
можно получить уравнение семейства профилей детали: (1.5)
(1.5)

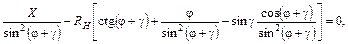
 (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8) (рис. 1.2.).
(рис. 1.2.). 




