Формообразованием поверхностей деталей машин на макроуровне занимались Семенченко И.И., Родин П.Р., Лашнев С.И., Цвис Ю.В., Сахаров Г.Н., Кирсанов Г.Н. и ряд других. В их работах формообразование любой поверхности детали при обработке режущим инструментом рассматривается как взаимоотношения двух тел абсолютно жестких при строго заданном относительном движении.
С целью унификации процесса моделирования поверхностей деталей и инструментов любая поверхность представляется как семейство отображений 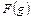 образующей поверхности
образующей поверхности  .
.
Для задания геометрического отображения 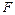 надо указать:
надо указать:
1. Некоторую фигуру (образующую)  , называемую областью значений отображения
, называемую областью значений отображения 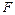 ;
;
2. Некоторую фигуру  , называемую областью отображения;
, называемую областью отображения;
3. Некоторые правила, сопоставляющие с каждой точкой  области
области  определенную точку
определенную точку  области
области  . Если данное отображение
. Если данное отображение 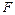 переводит точку
переводит точку  в точку
в точку  , то точку
, то точку  называют образом точки
называют образом точки  при отображении
при отображении 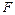 .
.
Отображение 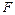 с областью определения
с областью определения  и областью значений
и областью значений  называется взаимно однозначным, если, во-первых, ни для каких двух точек
называется взаимно однозначным, если, во-первых, ни для каких двух точек  и
и  области
области  их образы
их образы  и
и  не совпадают и, во-вторых, каждая точка области является образом некоторой точки при отображении
не совпадают и, во-вторых, каждая точка области является образом некоторой точки при отображении 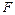 . В противном случае отображения не являются взаимно однозначными.
. В противном случае отображения не являются взаимно однозначными.
Основные правила, позволяющие сопоставить с каждой точкой  образующей
образующей  определенную точку
определенную точку  отображения образующей
отображения образующей  формулируются следующим образом:
формулируются следующим образом:
Пусть любая образующая, представляющая собой подмножество заданных точек  множества точек
множества точек  линии в плоскости
линии в плоскости  или в пространстве
или в пространстве  - соответственно обозначает двухмерное и трехмерное пространство), тогда для любой точки
- соответственно обозначает двухмерное и трехмерное пространство), тогда для любой точки  образом
образом  будет множество
будет множество 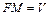 . Совокупность всех элементов
. Совокупность всех элементов  , являющихся образами
, являющихся образами  для всех
для всех  , назовем образом множества
, назовем образом множества  и обозначим
и обозначим  . Тогда по определению:
. Тогда по определению:
 .
.
Если образующая состоит из нескольких участков  , то
, то
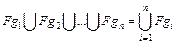
Множество отображений образующих  формируют поверхность:
формируют поверхность:
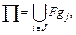
где  - интервал направляющей
- интервал направляющей  ;
;  - значение интервала или его величина, фиксированная от нулевой точки (рис. 1.13).
- значение интервала или его величина, фиксированная от нулевой точки (рис. 1.13).
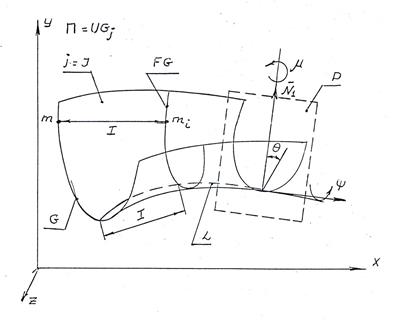
Рис. 1.13. Образующая поверхности детали
Положение образующей относительно направляющей фиксируется угловыми параметрами  .
.
Угол  определяет положение плоскости
определяет положение плоскости 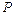 , в которой лежат образующая относительно вектора
, в которой лежат образующая относительно вектора  перпендикулярного к направляющей
перпендикулярного к направляющей  ; угол
; угол  фиксирует поворот этой плоскости вокруг нормали
фиксирует поворот этой плоскости вокруг нормали  ; угол
; угол  - поворот образующей относительно вектора
- поворот образующей относительно вектора  , касательного к направляющей; угол
, касательного к направляющей; угол  - поворот вокруг оси направляющей в случае сложной формы направляющей (например, винтовой линии).
- поворот вокруг оси направляющей в случае сложной формы направляющей (например, винтовой линии).
Угловые параметры  могут быть как фиксированными, так и переменными. В последнем случае взаимосвязь величины перемещения по линии
могут быть как фиксированными, так и переменными. В последнем случае взаимосвязь величины перемещения по линии  и поворотом плоскости
и поворотом плоскости 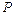 отображается параметрами:
отображается параметрами:
 ;
;  ;
;  ;
;  ;
;
где параметр 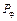 известен, как параметр винтового движения;
известен, как параметр винтового движения;  - шаг.
- шаг.
Остальные параметры определяются следующим образом.
Параметр  - параметр поступательно-вращательного движения, при котором направление вращения совпадает с направлением движения по направляющей и
- параметр поступательно-вращательного движения, при котором направление вращения совпадает с направлением движения по направляющей и  - шаг.
- шаг.
Параметр  - параметр поступательно-вращательного движения, при котором направление вращения нормально направлению перещения по направляющей и
- параметр поступательно-вращательного движения, при котором направление вращения нормально направлению перещения по направляющей и  - шаг.
- шаг.
Параметр  - параметр поступательно-вращательного движения с вращением вокруг направляющей и
- параметр поступательно-вращательного движения с вращением вокруг направляющей и  - шаг. В случае прямолинейной направляющей имеется равенство
- шаг. В случае прямолинейной направляющей имеется равенство 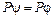 .
.
Величины  ,
,  ,
,  ,
,  определяются при вращении плоскости
определяются при вращении плоскости 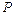 на угол
на угол 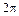 .
.
При перемещении по направляющей  формирование поверхности возможно посредством деформируемой образующей, степени деформации которой, обозначим через коэффициенты масштабирования
формирование поверхности возможно посредством деформируемой образующей, степени деформации которой, обозначим через коэффициенты масштабирования  ,
,  ,
,  в зависимости от направления деформации по координатным осям (или нормалям
в зависимости от направления деформации по координатным осям (или нормалям  ,
,  ). Величина коэффициентов масштабирования для каждого положения
). Величина коэффициентов масштабирования для каждого положения  является величиной переменной, и функция изменения этой величины может носить как линейный, так и нелинейный характер.
является величиной переменной, и функция изменения этой величины может носить как линейный, так и нелинейный характер.
Относительно направляющей  образующая
образующая  может иметь сдвиг под углом
может иметь сдвиг под углом 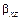 ,
,  ,
,  в соответствующих координатных плоскостях, что приводит к образованию новой образующей с формированием поверхности сдвига. Для изучения вопросов моделирования поверхностей детали и инструмента необходимо рассмотреть элементы теории графов.
в соответствующих координатных плоскостях, что приводит к образованию новой образующей с формированием поверхности сдвига. Для изучения вопросов моделирования поверхностей детали и инструмента необходимо рассмотреть элементы теории графов.

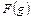 образующей поверхности
образующей поверхности  .
.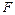 надо указать:
надо указать: , называемую областью отображения;
, называемую областью отображения; области
области  области
области  , то точку
, то точку  области
области  и
и  не совпадают и, во-вторых, каждая точка области является образом некоторой точки при отображении
не совпадают и, во-вторых, каждая точка области является образом некоторой точки при отображении  отображения образующей
отображения образующей  линии в плоскости
линии в плоскости  или в пространстве
или в пространстве  - соответственно обозначает двухмерное и трехмерное пространство), тогда для любой точки
- соответственно обозначает двухмерное и трехмерное пространство), тогда для любой точки  образом
образом 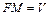 . Совокупность всех элементов
. Совокупность всех элементов  , являющихся образами
, являющихся образами  для всех
для всех  . Тогда по определению:
. Тогда по определению: .
. , то
, то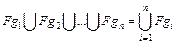
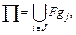
 - интервал направляющей
- интервал направляющей  ;
; 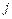 - значение интервала или его величина, фиксированная от нулевой точки (рис. 1.13).
- значение интервала или его величина, фиксированная от нулевой точки (рис. 1.13).
 .
. определяет положение плоскости
определяет положение плоскости 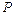 , в которой лежат образующая относительно вектора
, в которой лежат образующая относительно вектора  перпендикулярного к направляющей
перпендикулярного к направляющей  фиксирует поворот этой плоскости вокруг нормали
фиксирует поворот этой плоскости вокруг нормали  - поворот образующей относительно вектора
- поворот образующей относительно вектора  , касательного к направляющей; угол
, касательного к направляющей; угол  - поворот вокруг оси направляющей в случае сложной формы направляющей (например, винтовой линии).
- поворот вокруг оси направляющей в случае сложной формы направляющей (например, винтовой линии). могут быть как фиксированными, так и переменными. В последнем случае взаимосвязь величины перемещения по линии
могут быть как фиксированными, так и переменными. В последнем случае взаимосвязь величины перемещения по линии  ;
;  ;
;  ;
;  ;
;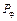 известен, как параметр винтового движения;
известен, как параметр винтового движения;  - шаг.
- шаг. - параметр поступательно-вращательного движения, при котором направление вращения совпадает с направлением движения по направляющей и
- параметр поступательно-вращательного движения, при котором направление вращения совпадает с направлением движения по направляющей и  - шаг.
- шаг. - параметр поступательно-вращательного движения, при котором направление вращения нормально направлению перещения по направляющей и
- параметр поступательно-вращательного движения, при котором направление вращения нормально направлению перещения по направляющей и  - шаг.
- шаг. - параметр поступательно-вращательного движения с вращением вокруг направляющей и
- параметр поступательно-вращательного движения с вращением вокруг направляющей и  - шаг. В случае прямолинейной направляющей имеется равенство
- шаг. В случае прямолинейной направляющей имеется равенство 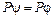 .
.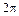 .
. ,
,  ,
,  в зависимости от направления деформации по координатным осям (или нормалям
в зависимости от направления деформации по координатным осям (или нормалям 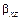 ,
,  ,
,  в соответствующих координатных плоскостях, что приводит к образованию новой образующей с формированием поверхности сдвига. Для изучения вопросов моделирования поверхностей детали и инструмента необходимо рассмотреть элементы теории графов.
в соответствующих координатных плоскостях, что приводит к образованию новой образующей с формированием поверхности сдвига. Для изучения вопросов моделирования поверхностей детали и инструмента необходимо рассмотреть элементы теории графов.


