Решение. 26 страница
Ответ: 2 7. B 15 № 77445. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Из рисунка видно, что наименьшее значение функции на заданном отрезке достигается в точке
Ответ: −25. Ответ: -25 8. B 15 № 77448. Найдите точку минимума функции
Решение. Найдём производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке −3 производная меняет знак с минуса на плюс, поэтому эта точка является точкой минимума. Ответ: −3. Ответ: -3 9. B 15 № 77492. Найдите точку максимума функции Решение. Найдем производную заданной функции:
На заданном промежутке (первая четверть без граничных точек) синус не обращается в нуль и принимает только положительные значения. Поэтому единственный нуль производной — число 1,5.
Определим знаки производной функции: она положительна при x < 1,5 и отрицательна при x > 1,5. Поэтому искомая точка максимума — число 1,5.
Ответ: 1,5. Ответ: 1,5 10. B 15 № 77476. Найдите наибольшее значение функции Вариант № 3656008 B 15 № 287203. Найдите наименьшее значение функции Решение. Квадратный трехчлен
Ответ: 7. Ответ: 7 2. B 15 № 77444. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: 3. Ответ: 3 B 15 № 286603. Найдите точку максимума функции Решение. Квадратный трехчлен
Ответ: 6. Ответ: 6 4. B 15 № 77461. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: 4. Ответ: 4 5. B 15 № 77443. Найдите точку максимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: −3. Ответ: -3 6. B 15 № 26691. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
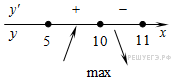
Определим знаки производной функции и изобразим на рисунке поведение функции:
Наименьшим значением заданной функции на отрезке
Ответ: −1. Ответ: -1 7. B 15 № 286803. Найдите наименьшее значение функции Решение. Выделим полный квадрат:
Отсюда имеем:
Поэтому наименьшее значние функции достигается в точке −11, и оно равно 1.
Ответ: 1. Ответ: 1 8. B 15 № 77477. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке Ответ: 1. Ответ: 1 9. B 15 № 26730. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Ответ: 5. Ответ: 5 10. B 15 № 503318. Найдите наибольшее значение функции Вариант № 3656078 1. B 15 № 245182. Найдите точку минимума функции Решение. Поскольку функция
Ответ: −1. Ответ: -1 B 15 № 287203. Найдите наименьшее значение функции Решение. Квадратный трехчлен
Ответ: 7. Ответ: 7 3. B 15 № 77426. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке
Ответ: 0. Ответ: 0 4. B 15 № 77485. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции на заданном отрезке:
В точке
Ответ: 4. Ответ: 4 5. B 15 № 129871. Найдите точку максимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: 18. Ответ: 18 6. B 15 № 132697. Найдите точку максимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: −3. Ответ: -3 7. B 15 № 77454. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Найденная производная неположительна на заданном отрезке, заданная функция убывает на нем, поэтому наименьшим значением функции на отрезке является Ответ: −8. Ответ: -8 8. B 15 № 77481. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке
Ответ: 10. Ответ: 10 9. B 15 № 77477. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке Ответ: 1. Ответ: 1 10. B 15 № 77429. Найдите наименьшее значение функции Вариант № 3707125 1. B 1. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды Решение. Всего на теплоходе 775 человек. Разделим 775 на 70:
Значит, на судне должно быть
Ответ: 12. Ответ: 12 2. B 1. Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Ответ округлите до целого числа. Решение. Если спидометр показывает скорость 65 миль в час, значит, в километрах это будет 65
Ответ: 105. Ответ: 105 3. B 1. Таксист за месяц проехал 6000 км. Стоимость 1 литра бензина — 20 рублей. Средний расход бензина на 100 км составляет 9 литров. Сколько рублей потратил таксист на бензин за этот месяц Решение. Средний расход бензина за месяц составил (6000: 100)
540 Значит, за месяц таксист потратил 10 800 рублей.
Ответ: 10 800. Ответ: 10800 4. B 1. Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков Александр платил за воду (холодную и горячую) ежемесячно 800 рублей. После установки счётчиков оказалось, что в среднем за месяц он расходует воды на 300 рублей при тех же тарифах на воду. За какое наименьшее количество месяцев при тех же тарифах на воду установка счётчиков окупится? Решение. Установка счетчиков позволяет ежемесячно экономить 800 − 300 = 500 руб. Значит, они окупятся через 3300: 500 = 6,6 месяца или за 7 полных месяцев. Ответ: 7 B 1. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 35 рублей за штуку. У Вани есть 160 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения? Решение. Разделим 160 на 35:
Ване хватает денег на 4 тюльпана, но цветов должно быть нечетное число. Следовательно, Ваня может купить букет из 3 тюльпанов.
Ответ: 3. Ответ: 3 6. B 1. В общежитии института в каждой комнате можно поселить четырех человек. Какое наименьшее количество комнат необходимо для поселения 83 иногородних студентов? Решение. Разделим 83 на 4:
Значит, для поселения 83 иногородних студентов необходима 21 комната.
Ответ: 21. Ответ: 21 7. B 1. Выпускники 11а покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 7 роз классному руководителю и директору. Они собираются подарить букеты 15 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы? Решение. Выпускники подарят 7 роз классному руководителю, 7 роз директору и по 3 розы оставшимся 13 учителям, т. е. еще 39 роз, всего 53 розы. Всего они потратят 53
Ответ: 1855. Ответ: 1855 8. B 1. В летнем лагере 218 детей и 26 воспитателей. В автобус помещается не более 45 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город? Решение. Всего в лагере 218 + 26 = 244 чел. Разделим 244 на 45:
Значит, чтобы перевезти всех из лагеря в город, понадобится 6 автобусов.
Ответ: 6. Ответ: 6 9. B 1. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения? Решение. Разделим 500 на 30:
Ване хватает денег на 16 тюльпанов, но цветов должно быть нечетное число. Следовательно, Ваня может купить букет из 15 тюльпанов.
Ответ: 15. Ответ: 15 10. B 1. На счету Машиного мобильного телефона было 53 рубля, а после разговора с Леной осталось 8 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 2 рубля 50 копеек? Вариант № 3707192 1. B 1. Выпускники 11а покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 7 роз классному руководителю и директору. Они собираются подарить букеты 15 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы? Решение. Выпускники подарят 7 роз классному руководителю, 7 роз директору и по 3 розы оставшимся 13 учителям, т. е. еще 39 роз, всего 53 розы. Всего они потратят 53
|

 на отрезке
на отрезке 
 .
.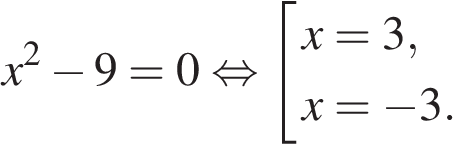

 . Оно равно
. Оно равно
 .
.


 , принадлежащую промежутку
, принадлежащую промежутку  .
. .
. на отрезке
на отрезке  .
.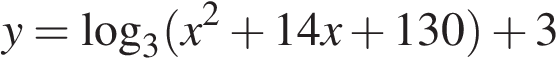 .
. с положительным старшим коэффициентом достигает наименьшего значения в точке
с положительным старшим коэффициентом достигает наименьшего значения в точке 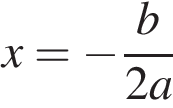 , в нашем случае — в точке −7. Функция
, в нашем случае — в точке −7. Функция 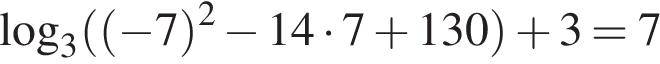 . Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции.
. Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции. .
.
 .
. , в нашем случае — в точке 6. Поскольку функция
, в нашем случае — в точке 6. Поскольку функция  возрастающая, а заданная функция определена при найденном значении переменной, она достигает максимума в той же точке, в которой достигает максимума подкоренное выражение.
возрастающая, а заданная функция определена при найденном значении переменной, она достигает максимума в той же точке, в которой достигает максимума подкоренное выражение. .
.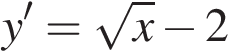 .
. .
.
 .
.
 .
. на отрезке
на отрезке 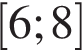 .
.


 .
. .
.

 на отрезке
на отрезке  .
.
 .
.

 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: 
 на отрезке
на отрезке  .
. Уравнение
Уравнение  не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является
не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является
 на отрезке
на отрезке  .
.
 возрастающая, заданная функция достигает минимума в той же точке, в которой достигает минимума выражение
возрастающая, заданная функция достигает минимума в той же точке, в которой достигает минимума выражение  . Квадратный трехчлен
. Квадратный трехчлен  , в нашем случае — в точке −1.
, в нашем случае — в точке −1. на отрезке
на отрезке  .
.

 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: .
. на отрезке
на отрезке  .
.




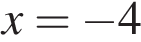 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: 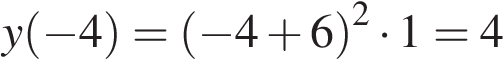
 .
. .
.

 .
. .
. .
.

 на отрезке
на отрезке  .
.


 .
. на отрезке
на отрезке  .
.


 .
. на отрезке
на отрезке  .
. .
. шлюпок.
шлюпок. 1,609 = 104,585 км в час.
1,609 = 104,585 км в час.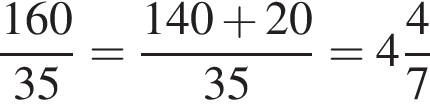 .
. .
. .
. .
.


