Решение. 24 страница
Ответ: −5. Ответ: -5 5. B 15 № 26695. Найдите наибольшее значение функции Решение. Найдем производную заданной функции: Следовательно, наибольшим значением функции на заданном отрезке является
Ответ: 5. Ответ: 5 6. B 15 № 77491. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: 1. Ответ: 1 7. B 15 № 77474. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найденная производная обращается в нуль в точках 3 и −3, из них на отрезке [−4; −1] лежит только точка −3.
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке
Ответ: −6. Ответ: -6 8. B 15 № 77453. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: 4. Ответ: 4 9. B 15 № 26722. Найдите точку максимума функции Решение. Функция определена и дифференцируема на
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: −4,5. Ответ: -4,5 10. B 15 № 77422. Найдите наибольшее значение функции Вариант № 3654717 1. B 15 № 26722. Найдите точку максимума функции Решение. Функция определена и дифференцируема на
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: −4,5. Ответ: -4,5 2. B 15 № 26699. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Следовательно, наибольшим значением функции на заданном отрезке является
Ответ: 32. Ответ: 32 3. B 15 № 77481. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке
Ответ: 10. Ответ: 10 4. B 15 № 26732. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: 2. Ответ: 2 5. B 15 № 26710. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: −17. Ответ: -17 6. B 15 № 77445. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Из рисунка видно, что наименьшее значение функции на заданном отрезке достигается в точке
Ответ: −25. Ответ: -25 7. B 15 № 77452. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке Ответ: −3. Ответ: -3 8. B 15 № 26713. Найдите точку максимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: −15. Ответ: -15 9. B 15 № 282861. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
В точке
Ответ: −1. Ответ: -1 10. B 15 № 77421. Найдите наименьшее значение функции
Вариант № 3654728 1. B 15. Найдите наименьшее значение функции Решение. Найдем производную заданной функции: Следовательно, наименьшим значением функции на заданном отрезке является
Ответ: 9. Ответ: 9 2. B 15. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной:
В точке
Ответ: −4. Ответ: -4 3. B 15. Найдите точку максимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума Ответ: −3. Ответ: -3 4. B 15. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Сделаем замену
Вернемся к исходной переменной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
На отрезке
Ответ: 48. Ответ: 48 5. B 15. Найдите наименьшее значение функции
Решение. Выделим полный квадрат:
Отсюда имеем:
Поэтому наименьшее значние функции достигается в точке 3, и оно равно 2.
Ответ: 2.
Примечание. Приведем другое решение.
Поскольку функция Ответ: 2 6. B 15. Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: 4. Ответ: 4 7. B 15. Найдите наименьшее значение функции Решение. Квадратный трехчлен
Ответ: 2. Ответ: 2 8. B 15. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Из уравнения
Определим знаки производной функции и изобразим на рисунке поведение функции:
На отрезке [−2; 0] функция убывает, поэтому она достигает своего наибольшего значения в точке x = −2. Найдем это наибольшее значение:
Ответ: 12. Ответ: 12 9. B 15. Найдите наибольшее значение функции Решение. Найдем производную заданной функции:
Найденная производная неотрицательна на заданном отрезке, заданная функция возрастает на нем, поэтому наибольшим значением функции на отрезке является
Ответ: 11. Ответ: 11 10. B 15 № 26705. Найдите наименьшее значение функции
Вариант № 3655569 1. B 15 № 286803. Найдите наименьшее значение функции Решение. Выделим полный квадрат:
Отсюда имеем:
Поэтому наименьшее значние функции достигается в точке −11, и оно равно 1.
Ответ: 1. Ответ: 1 2. B 15 № 26696. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Следовательно, наименьшим значением функции на заданном отрезке является
Ответ: 16. Ответ: 16 B 15 № 286703. Найдите точку минимума функции Решение. Квадратный трехчлен
Ответ: 14. Ответ: 14 B 15 № 286603. Найдите точку максимума функции Решение. Квадратный трехчлен
Ответ: 6. Ответ: 6 5. B 15 № 26714. Найдите наименьшее значение функции Решение. Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
|

 на отрезке
на отрезке  .
. Уравнение
Уравнение  не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей.
не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей.
 .
.


 .
. на отрезке
на отрезке  .
. .
.
 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: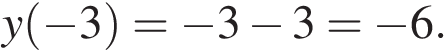
 .
.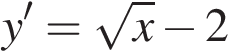 .
.

 .
. .
. . Найдем производную заданной функции:
. Найдем производную заданной функции:


 .
. на отрезке
на отрезке 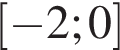
 на отрезке
на отрезке 
 Уравнение
Уравнение 
 на отрезке
на отрезке  .
.


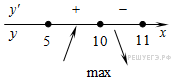
 функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: .
. .
.



 .
. .
.


 .
. на отрезке
на отрезке 
 .
.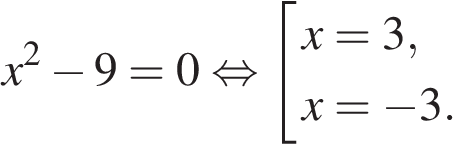

 . Оно равно
. Оно равно
 на отрезке
на отрезке  .
. .
.

 .
. .
.


 .
.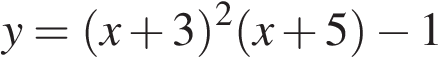 на отрезке
на отрезке 



 .
. на отрезке
на отрезке 
 на отрезке
на отрезке  .
. Уравнение
Уравнение 
 на отрезке
на отрезке  .
.
 .
. .
. .
. .
. .
.

 на отрезке
на отрезке  .
.
 и решим полученное уравнение:
и решим полученное уравнение:



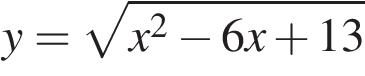


 возрастающая, а подкоренное выражение положительно при всех значениях переменной, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения подкоренное выражение. Квадратный трехчлен
возрастающая, а подкоренное выражение положительно при всех значениях переменной, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения подкоренное выражение. Квадратный трехчлен  с положительным старшим коэффициентом достигает наименьшего значения в точке
с положительным старшим коэффициентом достигает наименьшего значения в точке 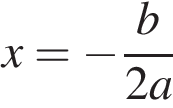 , в нашем случае — в точке 3, и оно равно 4. Следовательно, наименьшее значение заданной функции
, в нашем случае — в точке 3, и оно равно 4. Следовательно, наименьшее значение заданной функции  .
. .
.


 .
. . Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции.
. Поскольку логарифмическая функция с основанием, большим 1, возрастает, найденное значение является искомым наименьшим значением заданной функции. на отрезке
на отрезке  .
. найдем нули производной:
найдем нули производной: 


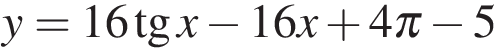 на отрезке
на отрезке  .
.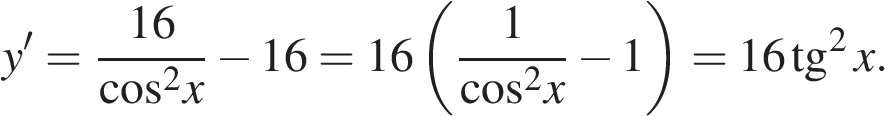

 на отрезке
на отрезке  .
.

 на отрезке
на отрезке  .
. . Найденная производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей.
. Найденная производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. .
. .
. , в нашем случае — в точке 14. Поскольку функция
, в нашем случае — в точке 14. Поскольку функция  .
. , в нашем случае — в точке 6. Поскольку функция
, в нашем случае — в точке 6. Поскольку функция  на отрезке
на отрезке  .
.



