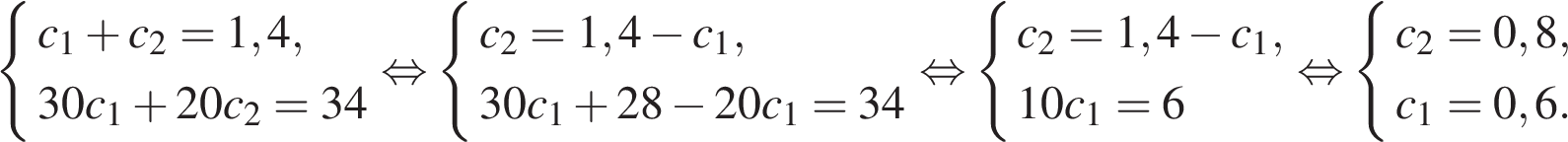Решение. 19 страница
4. B 14. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. Решение. Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть
Ответ: 88. Ответ: 88 5. B 14. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах. Решение. Скорость поезда равна
Ответ: 800. Ответ: 800 6. B 14. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно? Решение. Обозначим объем бака за 1. Тогда три насоса, работая вместе, заполнят бак за
Ответ: 10. Приведем другое решение. Первый насос за минуту наполняет одну двадцатую бака, второй — одну тридцатую, третий — одну шестидесятую. Работая вместе, за минуту они наполнят шесть шестидесятых или одну десятую бака. Значит, весь бак насосы наполнят за 10 минут.
Приведем другое решение. За один час первый насос наполнит 3 бака, второй — 2 бака, а третий — 1 бак. Работая вместе, за один час они 6 баков. Значит, один бак насосы наполнят в шесть раз быстрее, т. е. за 10 минут. Ответ: 10 7. B 14. Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней. Решение. Пусть рабочие в первый день проложили
Ответ: 97. Ответ: 97 8. B 14. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам. Решение. Пусть улитка проползла в первый день
Ответ: 30. Ответ: 30 9. B 14. Клиент А. сделал вклад в банке в размере 6200 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 682 рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам? Решение. Если в банк под
Тем самым, банк начислял 10 процентов годовых.
Ответ: 10. Ответ: 10 10. B 14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
Вариант № 3715278 1. B 14. Два велосипедиста одновременно отправились в 88–километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч. Решение. Пусть
Таким образом, скорость велосипедиста, пришедшего к финишу вторым, равна 8 км/ч. Ответ: 8. Ответ: 8 2. B 14. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на Решение. Обозначим первоначальную стоимость акций за 1. Пусть в понедельник акции компании подорожали на
Ответ: 20. Ответ: 20 3. B 14. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе? Решение. Наименьшее общее кратное чисел 9, 14 и 18 равно 126. За 126 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят 14 + 9 + 7 = 30 бассейнов. Следовательно, работая одновременно, первый, второй и третий насосы заполняют 15 бассейнов за 126 минут, а значит, 1 бассейн за 8,4 минуты.
Ответ: 8,4. Ответ: 8,4 4. B 14. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй – длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? Решение. пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
Пусть
Ответ: 6. Ответ: 6 5. B 14. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 5 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 5 км/ч больше скорости другого? Решение. Пусть
Следовательно,
Ответ: 30. Ответ: 30 6. B 14. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша? Решение. За минуту Маша пропалывает одну двадцатую грядки, а Маша с Дашей вместе — одну двенадцатую. Поэтому за одну минуту Даша пропалывает Ответ: 30. Ответ: 30 7. B 14. В 2008 году в городском квартале проживало Решение. В 2009 году число жителей стало
Ответ: 47088. Ответ: 47088 8. B 14. Расстояние между пристанями Решение. Скорость плота равна скорости течения реки 2 км/ч. Пусть
Ответ: 22. Ответ: 22 9. B 14. Расстояние между городами Решение. Пусть автомобили встретятся на расстоянии
Ответ: 240. Ответ: 240 10. B 14. Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?
Вариант № 3715436 1. B 14. Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой? Решение. Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой – 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до последней встречи часовая стрелка пройдет
Часовая стрелка пройдет 9 делений, что соответствует 9 часам или 540 минутам.
Ответ: 540.
По просьбам читателей помещаем общее решение. Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30 h + 0,5 m градусов, а минутная — на 6 m градусов относительно 12-часового деления. Пусть в первый раз стрелки встретятся через t 1 минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6 m + 6 t 1 = 30 h + 0,5 m + 0,5 t 1, т. е. t 1 = (60 h − 11 m)/11 (*). В противоположном случае получаем уравнение 6 m + 6 t 1 = 30 h + 0,5 m + 0,5 t 1 + 360, откуда t 1 = (60 h − 11 m + 720)/11 (**). Пусть во второй раз стрелки встретятся через t 2 минут после первого, тогда 0,5 t 2 = 6 t 2 − 360, откуда t 2 = 720/11 (***). Это же верно для каждого следующего оборота. Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: tn = (60 h − 11 m + 720(n − 1))/11 или tn = (60 h − 11 m + 720 n)/11. Ответ: 540 2. B 14. Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Решение. Пусть масса первого сплава
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ: 100. Ответ: 100 3. B 14. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч. Решение. Пусть
Значит, первым финишировал велосипедист, двигавшийся со скоростью 16 км/ч. Ответ: 16. Ответ: 16 4. B 14. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах. Решение. Относительная скорость поездов равна
За 36 секунд один поезд проходит мимо другого, то есть вместе поезда преодолевают расстояние, равное сумме их длин:
поэтому длина скорого поезда Ответ: 300. Ответ: 300 5. B 14. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч. Решение. Пусть
Таким образом, скорость велосипедиста была равна 10 км/ч. Ответ: 10. Ответ: 10 6. B 14. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч. Решение. Заметим, что время подъема составило 1 час 30 минут или 1,5 часа, а время спуска 1,25 часа. Пусть x км/ч — скорость движения пешехода на спуске, тогда х − 2 км/ч — скорость движения пешехода на подъеме, 1,25 х км — длина пути на спуске, 1,5(х − 2) км — длина пути на подъеме. Всего было пройдено 8 км, откуда имеем:
Тем самым, скорость пешехода на спуске была равна 4 км/ч.
Ответ: 4. Ответ: 4 7. B 14. Грузовик перевозит партию щебня массой 60 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 4 тонны щебня. Определите, сколько тонн щебня было перевезено за пятый день, если вся работа была выполнена за 8 дней. Решение. Пусть в первый день грузовик перевез
Имеем
Следовательно, за пятый день было перевезено 8 тонн щебня. Ответ: 8. Ответ: 8 8. B 14. Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде? Решение. Пусть концентрация первого раствора кислоты –
|

 км – весь путь автомобиля, тогда средняя скорость равна:
км – весь путь автомобиля, тогда средняя скорость равна: км/ч.
км/ч. . За 36 секунд поезд проходит мимо придорожного столба расстояние, равное своей длине:
. За 36 секунд поезд проходит мимо придорожного столба расстояние, равное своей длине: .
.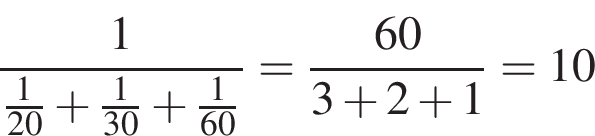 минут.
минут. метров тоннеля, во второй —
метров тоннеля, во второй —  , …, в последний —
, …, в последний —  метров тоннеля. Длина тоннеля
метров тоннеля. Длина тоннеля 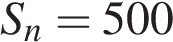 метров.
метров. 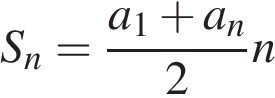 ,
, 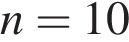 дней. Тогда в последний день рабочие проложили
дней. Тогда в последний день рабочие проложили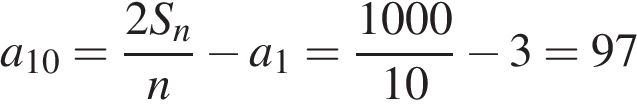 метров.
метров. метров. Тогда
метров. Тогда 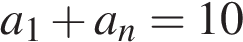 м, а за
м, а за  дней проползла
дней проползла  метров. Поскольку всего она проползла 150 метров, имеем:
метров. Поскольку всего она проползла 150 метров, имеем: 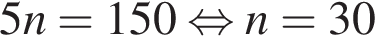 . Таким образом, улитка потратила на весь путь 30 дней.
. Таким образом, улитка потратила на весь путь 30 дней. процентов годовых положена сумма
процентов годовых положена сумма  , то через
, то через  Поэтому клиент А. за два года получил
Поэтому клиент А. за два года получил  руб., а клиент B. за год получил
руб., а клиент B. за год получил  По условию,
По условию,  откуда имеем:
откуда имеем:

 км/ч – скорость велосипедиста, пришедшего к финишу вторым, тогда скорость первого велосипедиста –
км/ч – скорость велосипедиста, пришедшего к финишу вторым, тогда скорость первого велосипедиста –  км/ч. Первый велосипедист прибыл к финишу на 3 часа раньше второго, отсюда имеем:
км/ч. Первый велосипедист прибыл к финишу на 3 часа раньше второго, отсюда имеем:
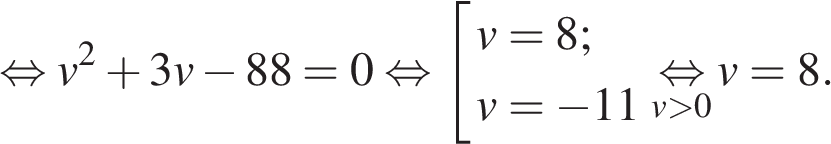
 дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник? , и их стоимость стала составлять
, и их стоимость стала составлять  . Во вторник акции подешевели на
. Во вторник акции подешевели на  . В результате они стали стоить на
. В результате они стали стоить на  .
. м.
м. – разность скоростей сухогрузов, тогда
– разность скоростей сухогрузов, тогда м/мин
м/мин  км/ч
км/ч км/ч. Пусть через
км/ч. Пусть через 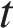 часов мотоциклисты поравняются в первый раз. Тогда, поскольку их разделяет 2,5 км (половина трассы) имеем:
часов мотоциклисты поравняются в первый раз. Тогда, поскольку их разделяет 2,5 км (половина трассы) имеем: .
. часа или 30 минут.
часа или 30 минут. грядки. Всю грядку она прополет за 30 минут.
грядки. Всю грядку она прополет за 30 минут. человек. В 2009 году, в результате строительства новых домов, число жителей выросло на
человек. В 2009 году, в результате строительства новых домов, число жителей выросло на  , а в 2010 году на
, а в 2010 году на  по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году? человек, а в 2010 году число жителей стало
человек, а в 2010 году число жителей стало 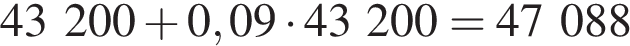 человек.
человек. и
и 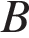 равно 120 км. Из
равно 120 км. Из  км/ч, а скорость яхты против течения равна
км/ч, а скорость яхты против течения равна  км/ч. Яхта, прибыв в пункт
км/ч. Яхта, прибыв в пункт 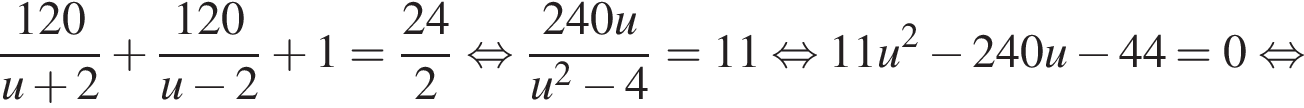
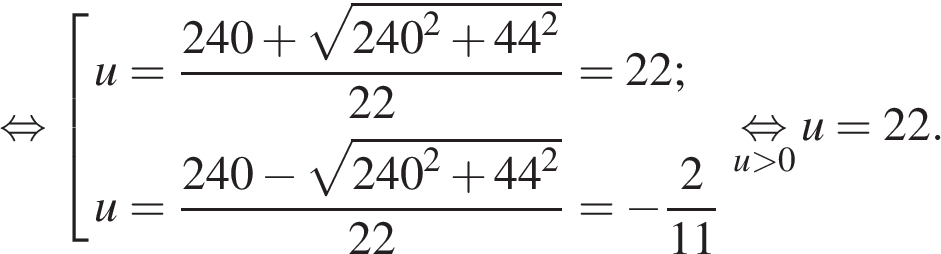
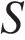 км от города
км от города  км. Второй автомобиль находился в пути на 1 час меньше первого, отсюда имеем:
км. Второй автомобиль находился в пути на 1 час меньше первого, отсюда имеем: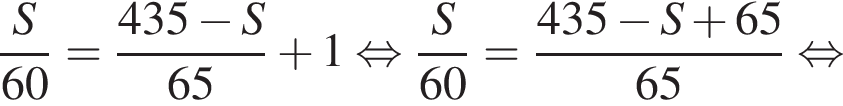
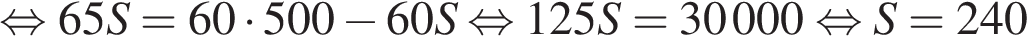 .
. делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок: .
. кг, а масса второго –
кг, а масса второго –  кг. Тогда массовое содержание никеля в первом и втором сплавах
кг. Тогда массовое содержание никеля в первом и втором сплавах  и
и  , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
, соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
 км/ч,
км/ч,  . Первый велосипедист прибыл к финишу на 1 час раньше второго, отсюда имеем:
. Первый велосипедист прибыл к финишу на 1 час раньше второго, отсюда имеем: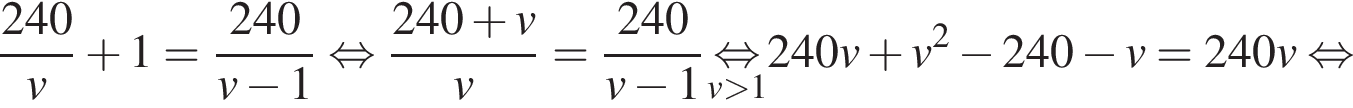
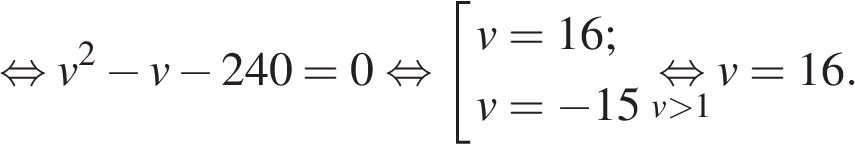

 м,
м,
 км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:
км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:
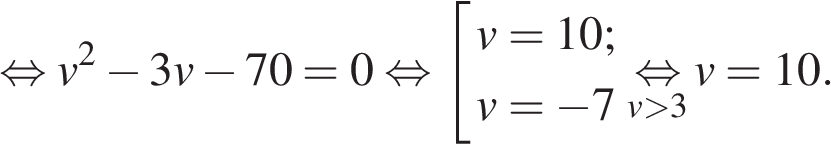
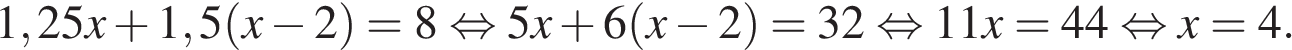
 тонны щебня, во второй —
тонны щебня, во второй —  тонн; всего было перевезено
тонн; всего было перевезено  тонн; норма перевозки увеличивалась ежедневно на
тонн; норма перевозки увеличивалась ежедневно на 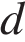 тонн. Поскольку
тонн. Поскольку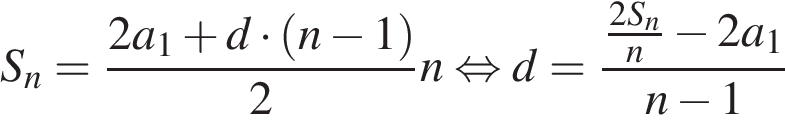 .
. .
. , а концентрация второго –
, а концентрация второго – 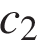 . Если смешать эти растворы кислоты, то получится раствор, содержащий 68% кислоты:
. Если смешать эти растворы кислоты, то получится раствор, содержащий 68% кислоты: 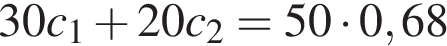 . Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты:
. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты: 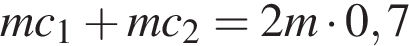 . Решим полученную систему уравнений:
. Решим полученную систему уравнений: