Ответ: 7.
Ответ: 7
6. B 13. 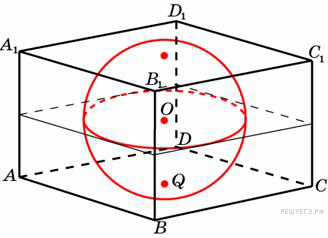 Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Решение.
Высота и сторона такого параллелепипеда равны диаметру сферы, то есть это куб со стороной 2. Площадь поверхности куба со стороной  :
:
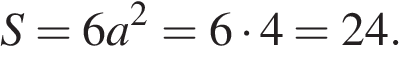
Ответ: 24.
Ответ: 24
7. B 13. 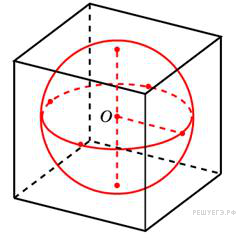 В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на  .
.
Решение.
Радиус вписанного в куб шара равен половине длины ребра:  . Тогда объем шара
. Тогда объем шара
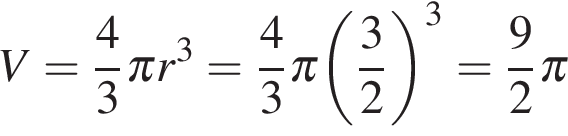 .
.
Ответ: 4,5.
Ответ: 4,5
8. B 13.  В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите угол
все ребра равны 1. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.
Рассмотрим прямоугольный треугольник  :
:
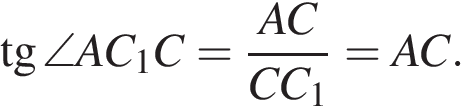
Осталось найти диагональ основания. В правильном шестиугольнике углы между сторонами равны  , тогда по теореме косинусов для треугольника АВС имеем:
, тогда по теореме косинусов для треугольника АВС имеем:

Так как  — острый, он равен
— острый, он равен 
Ответ: 60.
Ответ: 60
9. B 13.  Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Решение.
Объем куба  равен объему параллелепипеда
равен объему параллелепипеда

Значит, ребро куба

Ответ: 6.
Ответ: 6
10. B 13.  Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Вариант № 3714196
1. B 13. 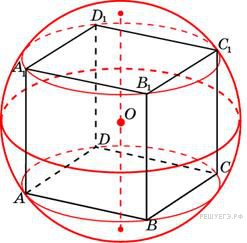 Около куба с ребром
Около куба с ребром  описан шар. Найдите объем этого шара, деленный на
описан шар. Найдите объем этого шара, деленный на  .
.
Решение.
Пусть длина ребра куба равна а, а его диагональ равна d. Радиус описанного шара R равен половине диагонали куба:
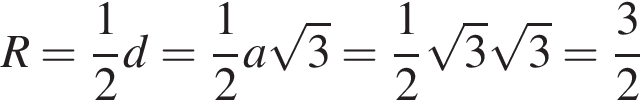 .
.
Поэтому объем шара равен
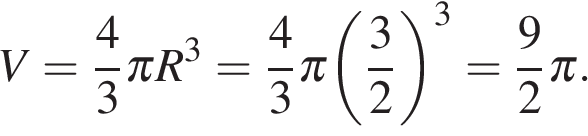
Тогда
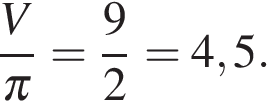
Ответ: 4,5.
Ответ: 4,5
2. B 13.  В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите тангенс угла
все ребра равны 1. Найдите тангенс угла 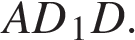
Решение.
Рассмотрим прямоугольный треугольник  катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:
катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:  . Поскольку
. Поскольку  имеем:
имеем:
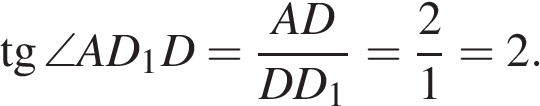
Ответ: 2.
Ответ: 2
3. B 13.  Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30  . В ответе укажите
. В ответе укажите  .
.
Решение.
Объем конуса равен
 ,
,
где  – площадь основания, а
– площадь основания, а 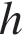 – высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в
– высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в  ° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
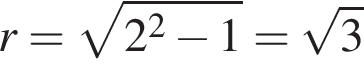 .
.
Тогда объем
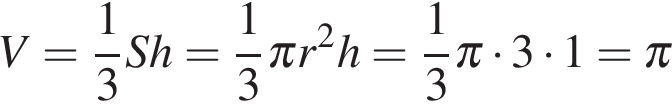 .
.
Ответ: 1.
Ответ: 1
4. B 13.  Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  .
.
Решение.
Найдем образующую по теореме Пифагора:  . Площадь полной поверхности конуса
. Площадь полной поверхности конуса
 .
.
Ответ: 24.
Ответ: 24
5. B 13.  Найдите объем
Найдите объем 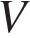 части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной части конуса равен
 .
.
Ответ: 607,5.
Ответ: 607,5
6. B 13.  Диагональ куба равна
Диагональ куба равна  . Найдите его объем.
. Найдите его объем.
Решение.
Диагональ куба в  раз больше его ребра. Поэтому ребро куба равно
раз больше его ребра. Поэтому ребро куба равно

Тогда объем куба  .
.
Ответ: 729.
Ответ: 729
7. B 13.  Гранью параллелепипеда является ромб со стороной 1 и острым углом 60
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60  . Одно из ребер параллелепипеда составляет с этой гранью угол в 60
. Одно из ребер параллелепипеда составляет с этой гранью угол в 60  и равно 2. Найдите объем параллелепипеда.
и равно 2. Найдите объем параллелепипеда.
Решение.
Объем параллелепипеда  , где
, где  – площадь одной из граней, а
– площадь одной из граней, а  – длина ребра, составляющего с этой гранью угол
– длина ребра, составляющего с этой гранью угол  . Площадь ромба с острым углом в
. Площадь ромба с острым углом в  равна двум площадям равностороннего треугольника. Вычислим объем:
равна двум площадям равностороннего треугольника. Вычислим объем:
 .
.
Ответ: 1,5.
Ответ: 1,5
8. B 13. 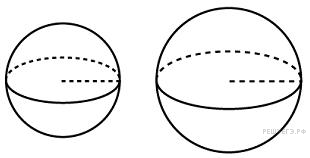 Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение.
Из условия 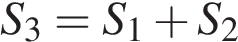 найдем, что радиус такого шара
найдем, что радиус такого шара
 .
.
Ответ: 10.
Ответ: 10
B 13.
В прямоугольном параллелепипеде 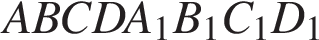 известно, что
известно, что 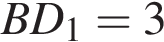 ,
,  ,
,  . Найдите длину ребра
. Найдите длину ребра  .
.
Решение.
 Найдем диагональ
Найдем диагональ 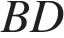 прямоугольника
прямоугольника  по теореме Пифагора:
по теореме Пифагора:
 .
.
Рассмотрим прямоугольный треугольник  . По теореме Пифагора
. По теореме Пифагора
 .
.
Ответ: 1.
Ответ: 1
10. B 13. 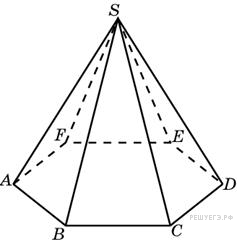 Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Решение.
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем высоту пирамиды по теореме Пифагора:  . Площадь основания
. Площадь основания
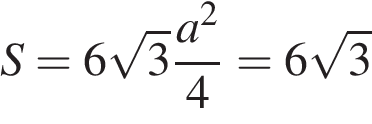 .
.
Тогда объем пирамиды
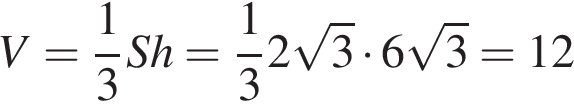 .
.
Ответ: 12.
Ответ: 12
Вариант № 3714293
1. B 13.  Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Решение.
Заметим, что
 .
.
Поскольку  , далее имеем:
, далее имеем:
 .
.
Ответ: 4,5.
Ответ: 4,5
2. B 13. 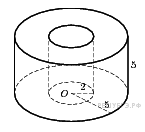 Найдите объем
Найдите объем 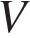 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
 .
.
Ответ: 105.
Ответ: 105
3. B 13.  Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Решение.
Объем прямоугольного параллелепипеда равен 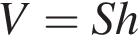 , где
, где  – площадь грани, а
– площадь грани, а 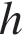 – высота перпендикулярного к ней ребра. Тогда площадь грани
– высота перпендикулярного к ней ребра. Тогда площадь грани
 .
.
Ответ: 8.
Ответ: 8
4. B 13. В прямоугольном параллелепипеде 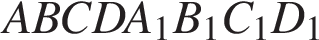 ребро
ребро  , ребро
, ребро  , ребро
, ребро  . Точка
. Точка  — середина ребра
— середина ребра  Найдите площадь сечения, проходящего через точки
Найдите площадь сечения, проходящего через точки 
 и
и  .
.
Решение.

Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому четырехугольник  — параллелограмм. Кроме того, ребро
— параллелограмм. Кроме того, ребро  перпендикулярно граням
перпендикулярно граням  и
и  , поэтому углы
, поэтому углы  и
и  — прямые. Следовательно, сечение
— прямые. Следовательно, сечение  — прямоугольник.
— прямоугольник.
Из прямоугольного треугольника  по теореме Пифагора найдем
по теореме Пифагора найдем 

Тогда площадь прямоугольника  равна:
равна:

Ответ:5.
Ответ: 5
5. B 13.  Найдите объем
Найдите объем 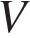 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной части цилиндра равен
 .
.
Ответ: 3,75.
Ответ: 3,75
6. B 13.  Диагональ куба равна
Диагональ куба равна  . Найдите его объем.
. Найдите его объем.
Решение.
Диагональ куба в  раз больше его ребра. Поэтому ребро куба равно
раз больше его ребра. Поэтому ребро куба равно

Тогда объем куба  .
.
Ответ: 729.
Ответ: 729
7. B 13. 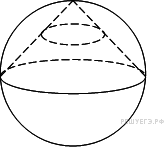
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Решение.
 ..
..
Ответ: 24.
Ответ: 24
8. B 13. В правильной четырехугольной пирамиде  точка
точка  — центр основания,
— центр основания,  вершина,
вершина,  ,
,  . Найдите длину отрезка
. Найдите длину отрезка  .
.
Решение.
 Рассмотрим треугольник
Рассмотрим треугольник  . Он прямоугольный, т. к.
. Он прямоугольный, т. к.  — высота, она перпендикулярна основанию
— высота, она перпендикулярна основанию  , а значит и прямой
, а значит и прямой  . Тогда по теореме Пифагора
. Тогда по теореме Пифагора
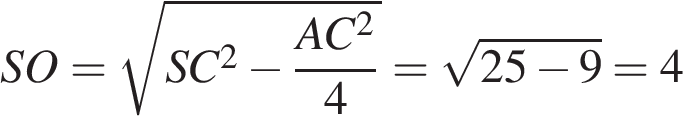 .
.
Ответ: 4.
Ответ: 4
9. B 13.  Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Решение.
Объем прямоугольного параллелепипеда равен 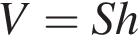 , где
, где  — площадь грани, а
— площадь грани, а 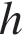 — высота перпендикулярного к ней ребра. Тогда
— высота перпендикулярного к ней ребра. Тогда
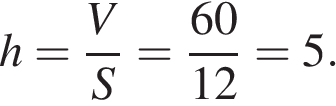
Ответ: 5.
Ответ: 5
10. B 13.  В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Решение.
Для вычисления боковой поверхности призмы воспользуемся формулой, где  – длина бокового ребра, а
– длина бокового ребра, а  – периметр перпендикулярного сечения призмы:
– периметр перпендикулярного сечения призмы:
 .
.
Ответ: 240.
Ответ: 240
Вариант № 3714356
1. B 13.  Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Решение.
Найдем третье ребро из выражения для объема:
 .
.
Площадь поверхности параллелепипеда
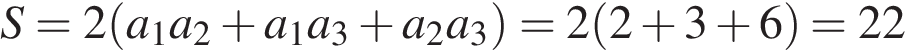 .
.
Ответ: 22.
Ответ: 22
2. B 13. В правильной четырехугольной пирамиде  точка
точка  — центр основания,
— центр основания,  вершина,
вершина,  ,
,  . Найдите длину отрезка
. Найдите длину отрезка  .
.
Решение.
 Рассмотрим треугольник
Рассмотрим треугольник  . Он прямоугольный: т. к.
. Он прямоугольный: т. к.  — высота, она перпендикулярна основанию
— высота, она перпендикулярна основанию  , а значит и прямой
, а значит и прямой  . Тогда по теореме Пифагора
. Тогда по теореме Пифагора
 .
.
Ответ: 6
3. B 13.  Около куба с ребром
Около куба с ребром  описан шар. Найдите объем этого шара, деленный на
описан шар. Найдите объем этого шара, деленный на  .
.
Решение.
Пусть длина ребра куба равна а, а его диагональ равна d. Радиус описанного шара R равен половине диагонали куба:
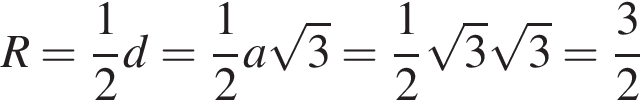 .
.
Поэтому объем шара равен
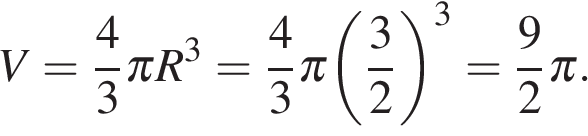
Тогда
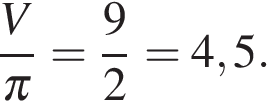
Ответ: 4,5.
Ответ: 4,5
4. B 13.  Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.
Решение.
Сторона правильного треугольника выражается через радиус описанной окружности как  . Площадь боковой поверхности призмы тогда равна
. Площадь боковой поверхности призмы тогда равна
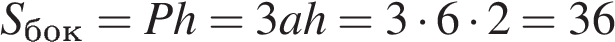 .
.
Ответ: 36.
Ответ: 36
5. B 13. 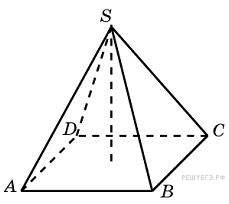 В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Решение.
По теореме Пифагора найдем, что половина диагонали основания равна 8. Тогда диагональ основания равна 16, а сторона – 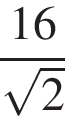 и площадь
и площадь
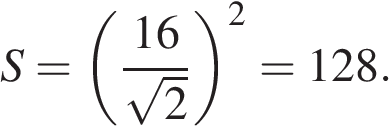
Тогда объем пирамиды
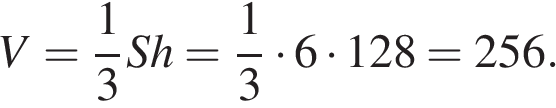
Ответ: 256.
Ответ: 256
6. B 13.  Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
Решение.
Объем пирамиды с площадью основания  и высотой
и высотой 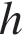 равен
равен
 .
.
Ответ: 24.
Ответ: 24
7. B 13.  Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Решение.
Высота и сторона такого параллелепипеда равны диаметру сферы, то есть это куб со стороной 2. Площадь поверхности куба со стороной  :
:
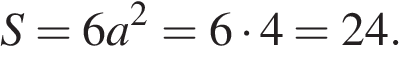
Ответ: 24.
Ответ: 24
8. B 13.  В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите тангенс угла
все ребра равны 1. Найдите тангенс угла 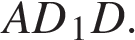

 Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. :
: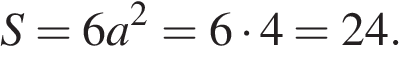
 В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на  .
. . Тогда объем шара
. Тогда объем шара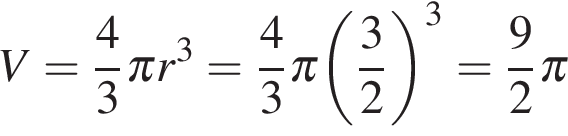 .
. В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите угол
все ребра равны 1. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. :
: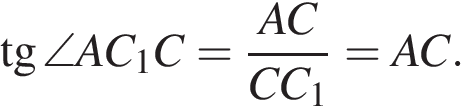
 , тогда по теореме косинусов для треугольника АВС имеем:
, тогда по теореме косинусов для треугольника АВС имеем:
 — острый, он равен
— острый, он равен 
 Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. равен объему параллелепипеда
равен объему параллелепипеда

 Около куба с ребром
Около куба с ребром  описан шар. Найдите объем этого шара, деленный на
описан шар. Найдите объем этого шара, деленный на 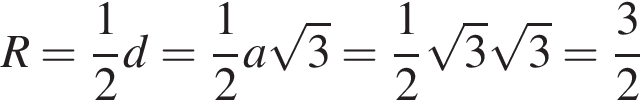 .
.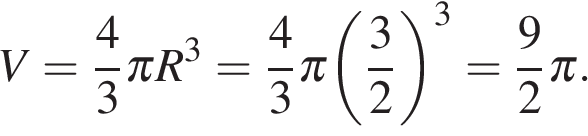
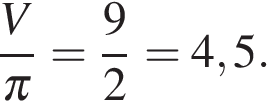
 В правильной шестиугольной призме
В правильной шестиугольной призме 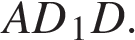
 катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:
катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:  . Поскольку
. Поскольку  имеем:
имеем: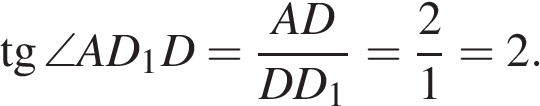
 Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30  . В ответе укажите
. В ответе укажите  .
. ,
, – площадь основания, а
– площадь основания, а 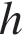 – высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в
– высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в  ° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора: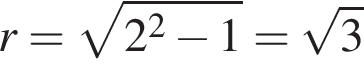 .
.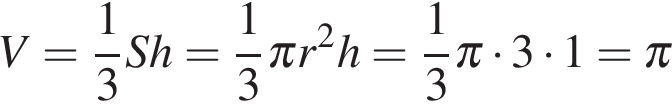 .
. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  . Площадь полной поверхности конуса
. Площадь полной поверхности конуса .
. Найдите объем
Найдите объем 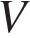 части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите  .
. .
. Диагональ куба равна
Диагональ куба равна  . Найдите его объем.
. Найдите его объем.
 .
. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60  , где
, где  – длина ребра, составляющего с этой гранью угол
– длина ребра, составляющего с этой гранью угол  . Площадь ромба с острым углом в
. Площадь ромба с острым углом в  равна двум площадям равностороннего треугольника. Вычислим объем:
равна двум площадям равностороннего треугольника. Вычислим объем: .
. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.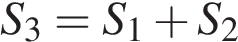 найдем, что радиус такого шара
найдем, что радиус такого шара .
.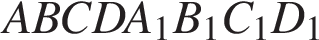 известно, что
известно, что 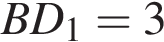 ,
,  ,
,  .
. Найдем диагональ
Найдем диагональ 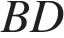 прямоугольника
прямоугольника  по теореме Пифагора:
по теореме Пифагора: .
. . По теореме Пифагора
. По теореме Пифагора .
. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды. . Площадь основания
. Площадь основания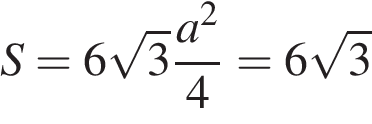 .
.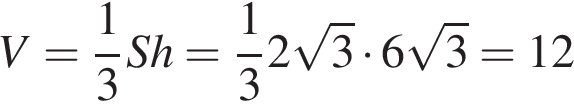 .
. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. .
. , далее имеем:
, далее имеем: .
. Найдите объем
Найдите объем  .
.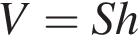 , где
, где  .
. , ребро
, ребро  , ребро
, ребро  . Точка
. Точка  — середина ребра
— середина ребра  Найдите площадь сечения, проходящего через точки
Найдите площадь сечения, проходящего через точки 
 и
и 
 — параллелограмм. Кроме того, ребро
— параллелограмм. Кроме того, ребро  перпендикулярно граням
перпендикулярно граням  и
и  , поэтому углы
, поэтому углы  и
и  — прямые. Следовательно, сечение
— прямые. Следовательно, сечение  по теореме Пифагора найдем
по теореме Пифагора найдем 


 Найдите объем
Найдите объем  .
.
 ..
.. точка
точка  — центр основания,
— центр основания,  ,
,  . Найдите длину отрезка
. Найдите длину отрезка  .
. Рассмотрим треугольник
Рассмотрим треугольник  . Он прямоугольный, т. к.
. Он прямоугольный, т. к.  . Тогда по теореме Пифагора
. Тогда по теореме Пифагора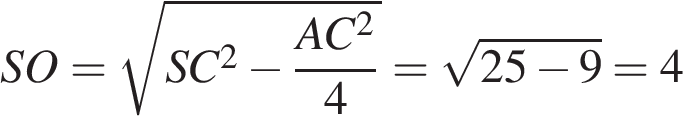 .
.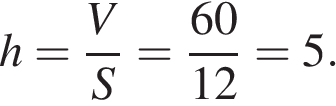
 В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы. – длина бокового ребра, а
– длина бокового ребра, а  – периметр перпендикулярного сечения призмы:
– периметр перпендикулярного сечения призмы: .
. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности. .
.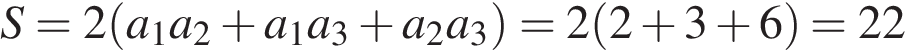 .
. ,
,  .
. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2.
, а высота равна 2. . Площадь боковой поверхности призмы тогда равна
. Площадь боковой поверхности призмы тогда равна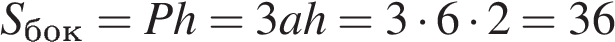 .
. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.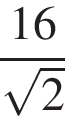 и площадь
и площадь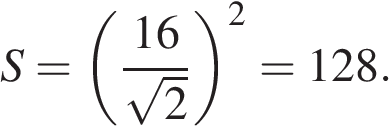
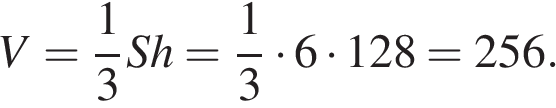
 Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4. .
.


