Решение.
Поскольку показатели максимальны, они равны 5. Подставим значения в формулу:
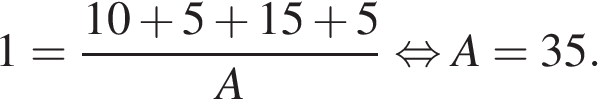
Ответ:35.
Ответ: 35
4. B 12. Находящийся в воде водолазный колокол, содержащий  моля воздуха при давлении
моля воздуха при давлении  атмосферы, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением
атмосферы, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где
(Дж), где  – постоянная,
– постоянная, 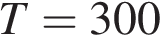 – температура воздуха,
– температура воздуха, 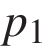 (атм) – начальное давление, а
(атм) – начальное давление, а  (атм) – конечное давление воздуха в колоколе. До какого наибольшего давления
(атм) – конечное давление воздуха в колоколе. До какого наибольшего давления  можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 6900 Дж? Ответ приведите в атмосферах.
можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 6900 Дж? Ответ приведите в атмосферах.
Решение.
Задача сводится к решению неравенства  при заданных значениях постоянной
при заданных значениях постоянной  , температуры воздуха
, температуры воздуха 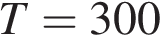 К, начального давления
К, начального давления  атм и количества воздуха
атм и количества воздуха  моль:
моль:
 атм.
атм.
Ответ: 6.
Ответ: 6
5. B 12. Уравнение процесса, в котором участвовал газ, записывается в виде  , где
, где 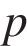 (Па) – давление в газе,
(Па) – давление в газе, 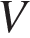 – объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
– объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
Решение.
Пусть 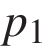 и
и  – начальные, а
– начальные, а  и
и  – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства
– конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства  , причем
, причем  :
:
 .
.
Ответ: 2.
Ответ: 2
6. B 12. Автомобиль, движущийся в начальный момент времени со скоростью  м/с, начал торможение с постоянным ускорением
м/с, начал торможение с постоянным ускорением  м/с2. За
м/с2. За 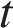 – секунд после начала торможения он прошёл путь
– секунд после начала торможения он прошёл путь  (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
Решение.
Найдем, за какое время 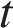 , прошедшее от момента начала торможения, автомобиль проедет 30 метров:
, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

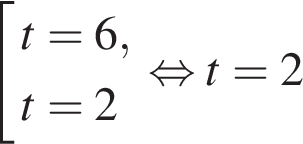 .
.
Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.
Ответ: 2.
Ответ: 2
7. B 12. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 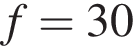 см. Расстояние
см. Расстояние  от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние
от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние  от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение  . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Решение.
Поскольку 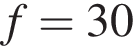 имеем:
имеем:
 .
.
Наименьшему возможному  значению соответствует наибольшее значение левой части полученного равенства, и, соответственно, наибольшее возможное значение правой части равенства. Разность
значению соответствует наибольшее значение левой части полученного равенства, и, соответственно, наибольшее возможное значение правой части равенства. Разность  в правой части равенства достигает наибольшего значения при наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при наименьшем значении вычитаемого  , которое достигается при наибольшем возможном значении знаменателя
, которое достигается при наибольшем возможном значении знаменателя  . Поэтому
. Поэтому  , откуда
, откуда
 см
см
По условию лампочка должна находиться на расстоянии от 30 до 50 см от линзы. Найденное значение  см удовлетворяет условию.
см удовлетворяет условию.
Ответ: 36.
Ответ: 36
8. B 12. Сила тока в цепи 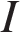 (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:
(в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 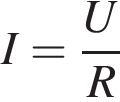 , где
, где 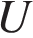 – напряжение в вольтах,
– напряжение в вольтах,  – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
– сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
Решение.
Задача сводится к решению неравенства  А при известном значении напряжения
А при известном значении напряжения  В:
В:
 Ом.
Ом.
Ответ: 55.
Ответ: 55
9. B 12. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением  , где
, где 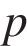 (атм.) – давление в газе,
(атм.) – давление в газе, 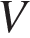 – объeм газа в литрах. Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
– объeм газа в литрах. Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
Решение.
пусть 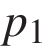 и
и  - начальные, а
- начальные, а  и
и  - конечные значения объема и давления газа, соответственно. Тогда задача сводится к решению неравенства
- конечные значения объема и давления газа, соответственно. Тогда задача сводится к решению неравенства
 , где
, где  атм.,
атм.,  л.,
л.,  атм.
атм.
Тогда
 .
.
Ответ: 0,05.
Ответ: 0,05
10. B 12. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле  , где
, где  – частота вынуждающей силы (в
– частота вынуждающей силы (в  ),
),  – постоянный параметр,
– постоянный параметр,  – резонансная частота. Найдите максимальную частоту
– резонансная частота. Найдите максимальную частоту  , меньшую резонансной, для которой амплитуда колебаний превосходит величину
, меньшую резонансной, для которой амплитуда колебаний превосходит величину  не более чем на
не более чем на  . Ответ выразите в
. Ответ выразите в  .
.
Вариант № 3712875
1. B 13. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Решение.
Объем такого шара
 ,
,
откуда получим, что  .
.
Ответ: 12.
Ответ: 12
2. B 13.  Найдите объем
Найдите объем 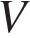 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной части цилиндра равен
 .
.
Ответ: 3,75.
Ответ: 3,75
3. B 13.  Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  .
.
Решение.
Найдем образующую по теореме Пифагора:  . Площадь полной поверхности конуса
. Площадь полной поверхности конуса
 .
.
Ответ: 24.
Ответ: 24
4. B 13. 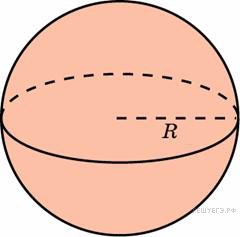 Объем шара равен 288
Объем шара равен 288  . Найдите площадь его поверхности, деленную на
. Найдите площадь его поверхности, деленную на  .
.
Решение.
Объем шара радиуса 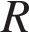 вычисляется по формуле
вычисляется по формуле 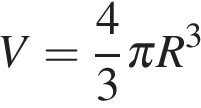 , откуда
, откуда
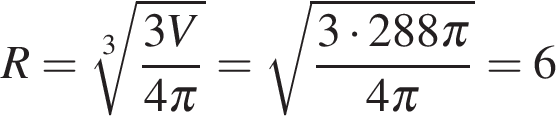 .
.
Площадь его поверхности:
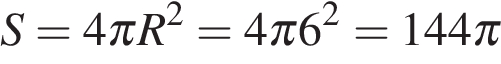 .
.
Ответ: 144.
Ответ: 144
5. B 13.  Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Решение.
Объем прямоугольного параллелепипеда равен 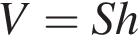 , где
, где  — площадь грани, а
— площадь грани, а 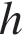 — высота перпендикулярного к ней ребра. Тогда
— высота перпендикулярного к ней ребра. Тогда
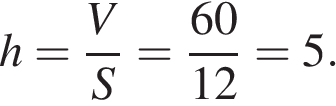
Ответ: 5.
Ответ: 5
6. B 13.  Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Решение.
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме попарных произведений его измерений
 .
.
Ответ: 22.
Ответ: 22
7. B 13.  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Решение.
Объем прямой призмы равен 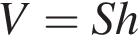 где
где  – площадь основания, а
– площадь основания, а 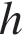 – боковое ребро. Тогда длина ее бокового ребра равна
– боковое ребро. Тогда длина ее бокового ребра равна
 .
.
Ответ: 4.
Ответ: 4
8. B 13.  Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на  .
.
Решение.
Радиус основания конуса  равен половине диагонали квадрата
равен половине диагонали квадрата  :
:  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на  :
:
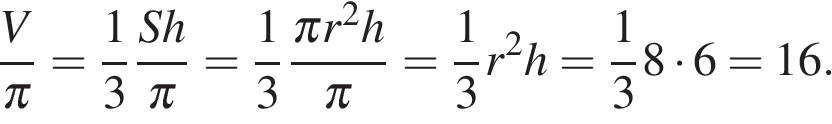
Ответ: 16.
Ответ: 16
9. B 13. 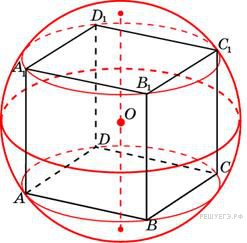 Около куба с ребром
Около куба с ребром  описан шар. Найдите объем этого шара, деленный на
описан шар. Найдите объем этого шара, деленный на  .
.
Решение.
Пусть длина ребра куба равна а, а его диагональ равна d. Радиус описанного шара R равен половине диагонали куба:
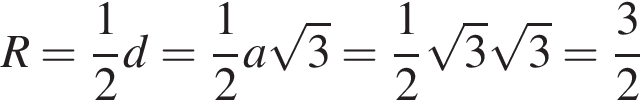 .
.
Поэтому объем шара равен
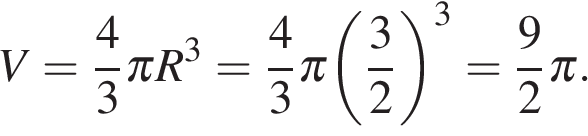
Тогда
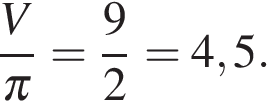
Ответ: 4,5.
Ответ: 4,5
B 13
. 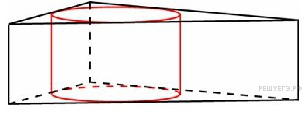
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.
Вариант № 3712978
1. B 13. 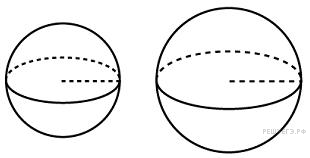 Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение.
Из условия 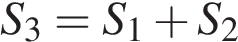 найдем, что радиус такого шара
найдем, что радиус такого шара
 .
.
Ответ: 10.
Ответ: 10
2. B 13.  В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите угол
все ребра равны 1. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.
Рассмотрим прямоугольный треугольник  :
:
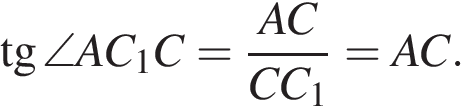
Осталось найти диагональ основания. В правильном шестиугольнике углы между сторонами равны  , тогда по теореме косинусов для треугольника АВС имеем:
, тогда по теореме косинусов для треугольника АВС имеем:

Так как  — острый, он равен
— острый, он равен 
Ответ: 60.
Ответ: 60
3. B 13.  Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на  .
.
Решение.
По теореме Пифагора найдем, что радиус основания равен  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на  :
:
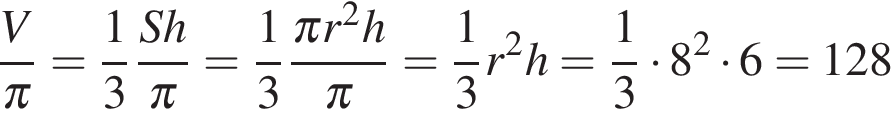
Ответ: 128.
Ответ: 128
4. B 13. В правильной четырёхугольной пирамиде  с основанием
с основанием  боковое ребро
боковое ребро  равно 5, сторона основания равна
равно 5, сторона основания равна  . Найдите объём пирамиды.
. Найдите объём пирамиды.
Решение.
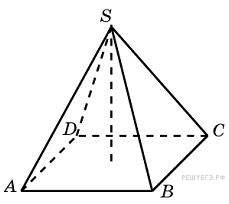
В основании правильной четырехугольной пирамиды лежит квадрат, вершина пирамиды проецируется в его центр. Введем обозначения, как показано на рисунке. Диагонали квадрата перпендикулярны друг другу, треугольник  прямоугольный и равнобедренный. В нем
прямоугольный и равнобедренный. В нем
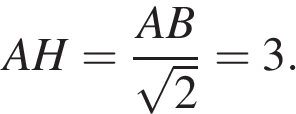
Тогда из прямоугольного треугольника  находим, что
находим, что
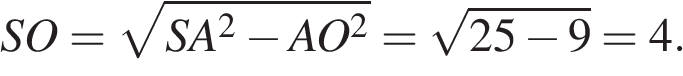
Откуда для объема пирамиды имеем:
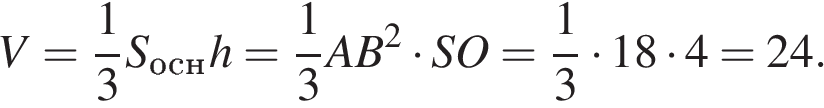
Ответ: 24.
Ответ: 24
5. B 13.  Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Решение.
Площадь пирамиды равна
 .
.
Площадь боковой стороны пирамиды  . Высоту треугольника
. Высоту треугольника 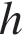 найдем по теореме Пифагора:
найдем по теореме Пифагора:  . Тогда площадь поверхности пирамиды
. Тогда площадь поверхности пирамиды
 .
.
Ответ: 340.
Ответ: 340
6. B 13.  Найдите угол
Найдите угол  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого  ,
,  ,
,  . Дайте ответ в градусах.
. Дайте ответ в градусах.
Решение.
В прямоугольнике  отрезок
отрезок  является диагональю,
является диагональю,  По теореме Пифагора
По теореме Пифагора

Прямоугольный треугольник  равнобедренный:
равнобедренный:  , значит, его острые углы равны
, значит, его острые углы равны 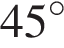
Ответ: 45.
Ответ: 45
7. B 13.  Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Решение.
Вершина правильной пирамиды проецируется в центр ее основания. В правильном шестиугольнике со стороной  расстояние от его центра до стороны равно радиусу вписанной окружности, который равен
расстояние от его центра до стороны равно радиусу вписанной окружности, который равен  . Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна
. Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна  . Тогда имеем:
. Тогда имеем:
 .
.
Ответ: 48.
Ответ: 48
8. B 13. 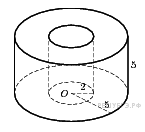 Найдите объем
Найдите объем 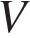 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
 .
.
Ответ: 105.
Ответ: 105
9. B 13.  В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Решение.
По теореме Пифагора найдем, что половина диагонали основания равна 8. Тогда диагональ основания равна 16, а сторона – 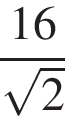 и площадь
и площадь
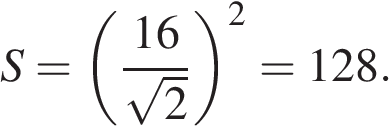
Тогда объем пирамиды
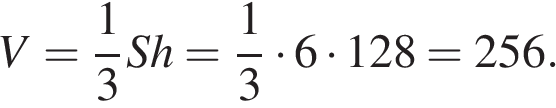
Ответ: 256.
Ответ: 256
10. B 13.  Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен  .
.

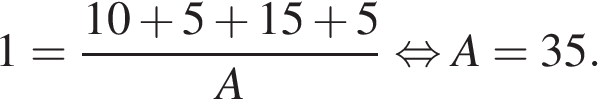
 моля воздуха при давлении
моля воздуха при давлении  атмосферы, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением
атмосферы, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где
(Дж), где  – постоянная,
– постоянная, 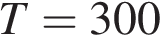 – температура воздуха,
– температура воздуха, 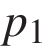 (атм) – начальное давление, а
(атм) – начальное давление, а  (атм) – конечное давление воздуха в колоколе. До какого наибольшего давления
(атм) – конечное давление воздуха в колоколе. До какого наибольшего давления  при заданных значениях постоянной
при заданных значениях постоянной  , температуры воздуха
, температуры воздуха  атм.
атм. , где
, где 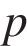 (Па) – давление в газе,
(Па) – давление в газе, 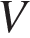 – объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
– объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза? – начальные, а
– начальные, а  – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства
– конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства  , причем
, причем  :
: .
. м/с, начал торможение с постоянным ускорением
м/с, начал торможение с постоянным ускорением  м/с2. За
м/с2. За 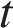 – секунд после начала торможения он прошёл путь
– секунд после начала торможения он прошёл путь  (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
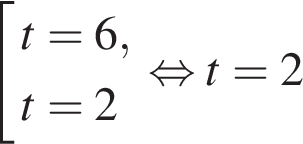 .
.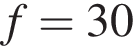 см. Расстояние
см. Расстояние  от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние
от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние  от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение  . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах. .
. в правой части равенства достигает наибольшего значения при наименьшем значении вычитаемого
в правой части равенства достигает наибольшего значения при наименьшем значении вычитаемого  , которое достигается при наибольшем возможном значении знаменателя
, которое достигается при наибольшем возможном значении знаменателя  , откуда
, откуда см
см см удовлетворяет условию.
см удовлетворяет условию.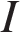 (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:
(в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 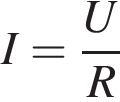 , где
, где 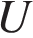 – напряжение в вольтах,
– напряжение в вольтах,  – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
– сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах. А при известном значении напряжения
А при известном значении напряжения  В:
В: Ом.
Ом. , где
, где  , где
, где  атм.,
атм.,  л.,
л.,  атм.
атм. .
. , где
, где  – частота вынуждающей силы (в
– частота вынуждающей силы (в  ),
),  – постоянный параметр,
– постоянный параметр,  – резонансная частота. Найдите максимальную частоту
– резонансная частота. Найдите максимальную частоту  . Ответ выразите в
. Ответ выразите в  ,
, .
. Найдите объем
Найдите объем 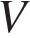 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
. .
. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  .
. . Площадь полной поверхности конуса
. Площадь полной поверхности конуса .
. Объем шара равен 288
Объем шара равен 288 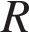 вычисляется по формуле
вычисляется по формуле 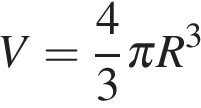 , откуда
, откуда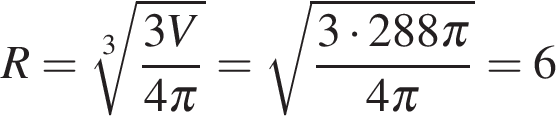 .
.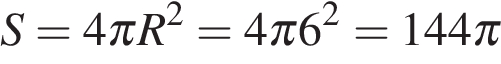 .
. Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.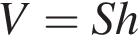 , где
, где  — площадь грани, а
— площадь грани, а 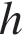 — высота перпендикулярного к ней ребра. Тогда
— высота перпендикулярного к ней ребра. Тогда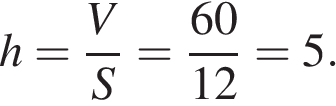
 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности. .
. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. .
. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на  равен половине диагонали квадрата
равен половине диагонали квадрата  :
:  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на 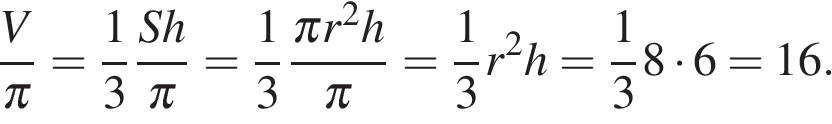
 Около куба с ребром
Около куба с ребром  описан шар. Найдите объем этого шара, деленный на
описан шар. Найдите объем этого шара, деленный на 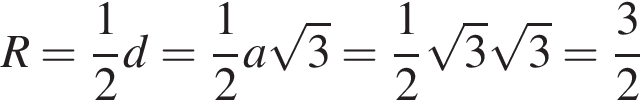 .
.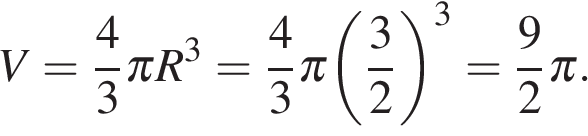
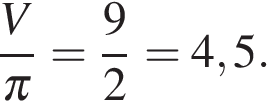

 Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.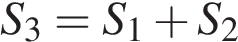 найдем, что радиус такого шара
найдем, что радиус такого шара .
. В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите угол
все ребра равны 1. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах. :
: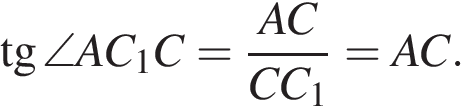
 , тогда по теореме косинусов для треугольника АВС имеем:
, тогда по теореме косинусов для треугольника АВС имеем:
 — острый, он равен
— острый, он равен 
 Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на
Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на 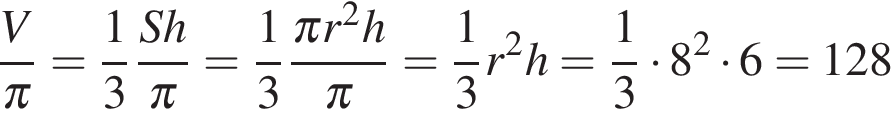
 с основанием
с основанием  равно 5, сторона основания равна
равно 5, сторона основания равна  . Найдите объём пирамиды.
. Найдите объём пирамиды.
 прямоугольный и равнобедренный. В нем
прямоугольный и равнобедренный. В нем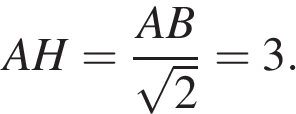
 находим, что
находим, что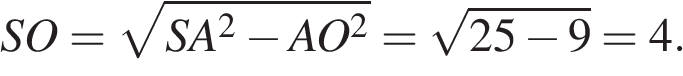
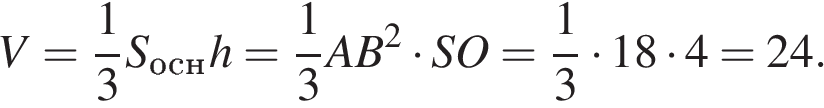
 Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. .
. . Высоту треугольника
. Высоту треугольника  . Тогда площадь поверхности пирамиды
. Тогда площадь поверхности пирамиды .
. Найдите угол
Найдите угол  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого  ,
,  ,
,  . Дайте ответ в градусах.
. Дайте ответ в градусах. отрезок
отрезок  является диагональю,
является диагональю,  По теореме Пифагора
По теореме Пифагора
 равнобедренный:
равнобедренный:  , значит, его острые углы равны
, значит, его острые углы равны 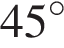
 Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45  . Найдите объем пирамиды.
. Найдите объем пирамиды. расстояние от его центра до стороны равно радиусу вписанной окружности, который равен
расстояние от его центра до стороны равно радиусу вписанной окружности, который равен  . Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна
. Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна  . Тогда имеем:
. Тогда имеем: .
. Найдите объем
Найдите объем  .
.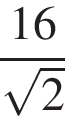 и площадь
и площадь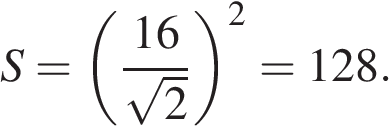
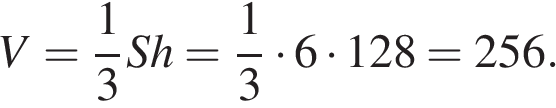
 Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен 


