Решение.
Найдем, за какое время 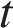 , прошедшее от момента начала торможения, автомобиль проедет 30 метров:
, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

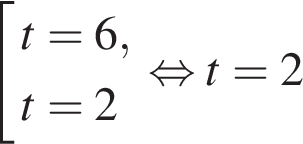 .
.
Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.
Ответ: 2.
Ответ: 2
7. B 12. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время 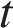 падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле
падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле 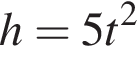 , где
, где  – расстояние в метрах,
– расстояние в метрах, 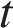 – время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
– время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Решение.
Пусть 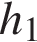 – расстояние до воды до дождя,
– расстояние до воды до дождя,  – расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным
– расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным 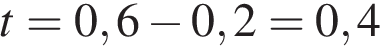 с. Уровень воды поднимется на
с. Уровень воды поднимется на  метров.
метров.
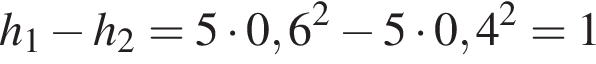
Ответ: 1.
Ответ: 1
8. B 12. Высота над землeй подброшенного вверх мяча меняется по закону 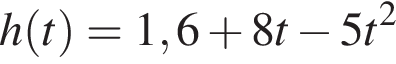 , где
, где  – высота в метрах,
– высота в метрах, 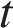 – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
– время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
Решение.
Определим моменты времени, когда мяч находился на высоте ровно три метра. Для этого решим уравнение  :
:
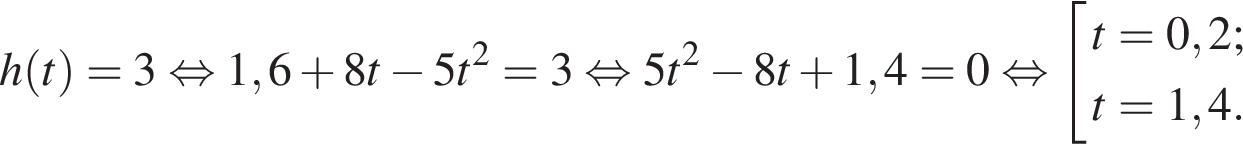
Проанализируем полученный результат: поскольку по условию задачи мяч брошен снизу вверх, это означает, что в момент времени 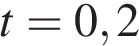 (с) мяч находился на высоте 3 метра, двигаясь снизу вверх, а в момент времени
(с) мяч находился на высоте 3 метра, двигаясь снизу вверх, а в момент времени 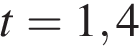 (с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее трёх метров 1,2 секунды.
(с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее трёх метров 1,2 секунды.
Ответ: 1,2.
Ответ: 1,2
9. B 12. Мотоциклист, движущийся по городу со скоростью  км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением
км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 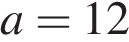 км/ч
км/ч  . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением
. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 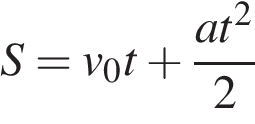 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Решение.
Мотоциклист будет находиться в зоне функционирования сотовой связи, если 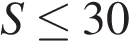 км. Задача сводится к нахождению наибольшего решения неравенства
км. Задача сводится к нахождению наибольшего решения неравенства 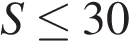 км при заданных значениях параметров
км при заданных значениях параметров  и
и 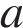 :
:

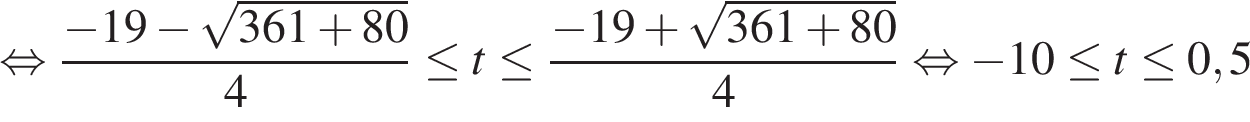
Учитывая то, что время – неотрицательная величина, получаем 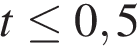 ч, то есть
ч, то есть 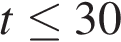 мин.
мин.
Ответ: 30.
Ответ: 30
10. B 12. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной  км с постоянным ускорением
км с постоянным ускорением 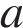 км/ч 2, вычисляется по формуле
км/ч 2, вычисляется по формуле  . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
Вариант № 3711816
1. B 12. Уравнение процесса, в котором участвовал газ, записывается в виде  , где
, где 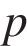 (Па) — давление в газе,
(Па) — давление в газе, 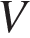 — объeм газа в кубических метрах,
— объeм газа в кубических метрах, 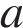 — положительная константа. При каком наименьшем значении константы
— положительная константа. При каком наименьшем значении константы 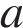 увеличение в 3 раза объeма газа, участвующего в этом процессе, приводит к уменьшению давления не менее, чем в 27 раз?
увеличение в 3 раза объeма газа, участвующего в этом процессе, приводит к уменьшению давления не менее, чем в 27 раз?
Решение.
Пусть 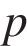 и
и 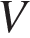 – начальные, а
– начальные, а 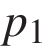 и
и  – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства
– конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства 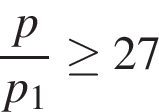 , причем
, причем 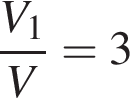 :
:
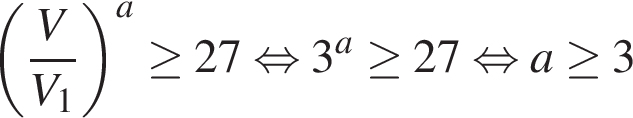 .
.
Значит, наименьшее значение константы 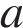 равно 3.
равно 3.
Ответ: 3.
Ответ: 3
2. B 12. Скорость колеблющегося на пружине груза меняется по закону  (см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
(см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Решение.
Задача сводится к решению неравенства 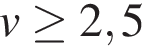 cм/с при заданном законе изменения скорости
cм/с при заданном законе изменения скорости  :
:

Таким образом, 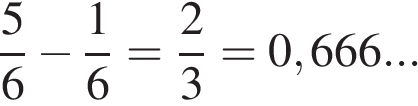 первой секунды после начала движения скорость груза превышала 2,5 см/с. Округляя, получаем 0,67.
первой секунды после начала движения скорость груза превышала 2,5 см/с. Округляя, получаем 0,67.
Ответ: 0,67.
Ответ: 0,67
3. B 12. Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью  м/с под острым углом
м/с под острым углом  к рельсам. От толчка платформа начинает ехать со скоростью
к рельсам. От толчка платформа начинает ехать со скоростью  (м/с), где
(м/с), где  кг – масса скейтбордиста со скейтом, а
кг – масса скейтбордиста со скейтом, а  кг – масса платформы. Под каким максимальным углом
кг – масса платформы. Под каким максимальным углом  (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?
(в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?
Решение.
Задача сводится к решению неравенства 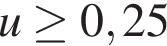 на интервале
на интервале  при заданных значениях массы скейтбордиста
при заданных значениях массы скейтбордиста  кг и массы платформы
кг и массы платформы  кг:
кг:
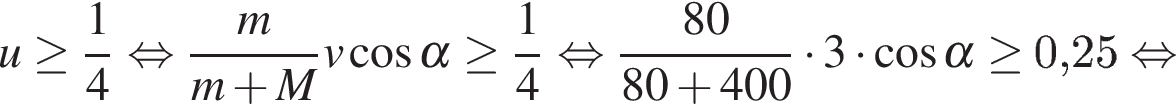
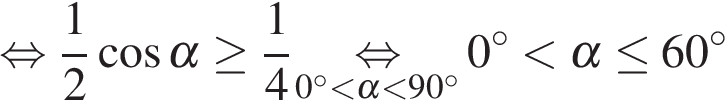 .
.
Ответ: 60.
Ответ: 60
4. B 12. Очень лeгкий заряженный металлический шарик зарядом 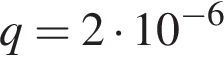 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет
Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет  м/с, на него начинает действовать постоянное магнитное поле, вектор индукции
м/с, на него начинает действовать постоянное магнитное поле, вектор индукции 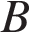 которого лежит в той же плоскости и составляет угол
которого лежит в той же плоскости и составляет угол  с направлением движения шарика. Значение индукции поля
с направлением движения шарика. Значение индукции поля  Тл. При этом на шарик действует сила Лоренца, равная
Тл. При этом на шарик действует сила Лоренца, равная  (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла
(Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла  шарик оторвeтся от поверхности, если для этого нужно, чтобы сила
шарик оторвeтся от поверхности, если для этого нужно, чтобы сила  была не менее чем
была не менее чем 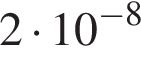 Н? Ответ дайте в градусах.
Н? Ответ дайте в градусах.
Решение.
Задача сводится к решению неравенства 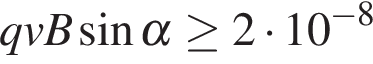 на интервале
на интервале 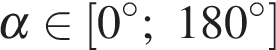 при заданных значениях заряда шарика
при заданных значениях заряда шарика 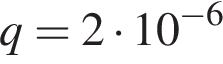 Кл, индукции магнитного поля
Кл, индукции магнитного поля 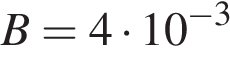 Тл и скорости
Тл и скорости  м/с:
м/с:
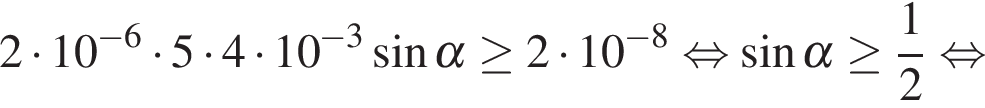
 .
.
Ответ: 30.
Ответ: 30
5. B 12. Мяч бросили под углом  к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле
к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле 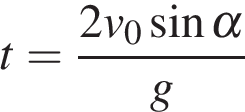 . При каком наименьшем значении угла
. При каком наименьшем значении угла  (в градусах) время полeта будет не меньше 3 секунд, если мяч бросают с начальной скоростью
(в градусах) время полeта будет не меньше 3 секунд, если мяч бросают с начальной скоростью  м/с? Считайте, что ускорение свободного падения
м/с? Считайте, что ускорение свободного падения  м/с
м/с  .
.
Решение.
Задача сводится к решению неравенства  на интервале
на интервале  при заданных значениях начальной скорости и ускорения свободного падения:
при заданных значениях начальной скорости и ускорения свободного падения:
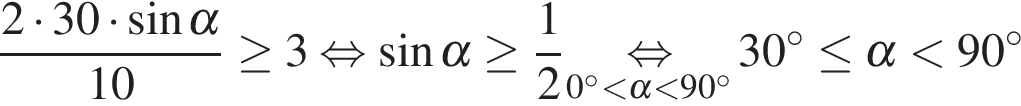 .
.
Ответ: 30.
Ответ: 30
6. B 12. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной  км с постоянным ускорением
км с постоянным ускорением  , вычисляется по формуле
, вычисляется по формуле  . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,7 километра, приобрести скорость не менее 105 км/ч. Ответ выразите в км/ч
. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,7 километра, приобрести скорость не менее 105 км/ч. Ответ выразите в км/ч  .
.
Решение.
Найдём, при каком ускорении гонщик достигнет требуемой скорости, проехав 0,7 километра. Задача сводится к решению уравнения  при известном значении длины пути
при известном значении длины пути 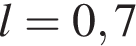 км:
км:
 км/ч2.
км/ч2.
Если его ускорение будет превосходить найденное, то, проехав один километр, гонщик наберёт большую скорость, поэтому наименьшее необходимое ускорение равно 7875 км/ч2.
Ответ: 7875.
Ответ: 7875
7. B 12. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время 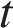 падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле
падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле 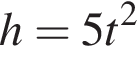 , где
, где  – расстояние в метрах,
– расстояние в метрах, 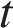 – время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
– время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Решение.
Пусть 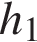 – расстояние до воды до дождя,
– расстояние до воды до дождя,  – расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным
– расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным 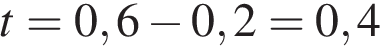 с. Уровень воды поднимется на
с. Уровень воды поднимется на  метров.
метров.
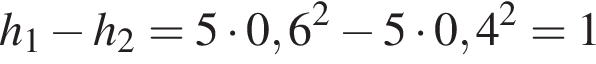
Ответ: 1.
Ответ: 1
8. B 12. В розетку электросети подключены приборы, общее сопротивление которых составляет  Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление
Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление 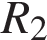 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями
этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями 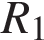 Ом и
Ом и 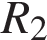 Ом их общее сопротивление даeтся формулой
Ом их общее сопротивление даeтся формулой  (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ (в омах.)
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ (в омах.)
Решение.
Задача сводится к решению неравенства 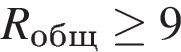 Ом при известном значении сопротивления приборов
Ом при известном значении сопротивления приборов 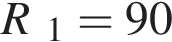 Ом:
Ом:
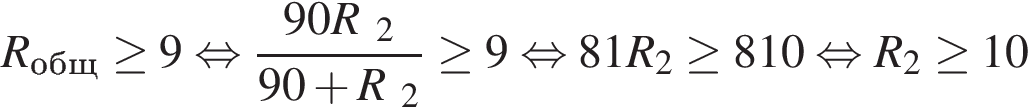 Ом.
Ом.
Ответ: 10.
Ответ: 10
9. B 12. Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела  , измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры:
, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры:  , где
, где  – постоянная, площадь
– постоянная, площадь 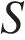 измеряется в квадратных метрах, а температура
измеряется в квадратных метрах, а температура 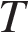 – в градусах Кельвина. Известно, что некоторая звезда имеет площадь
– в градусах Кельвина. Известно, что некоторая звезда имеет площадь  м
м  , а излучаемая ею мощность
, а излучаемая ею мощность  не менее
не менее 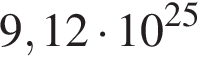 Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Решение.
Задача сводится к нахождению наименьшего решения неравенства 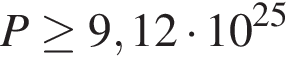 при известном значениях постоянной
при известном значениях постоянной  и заданной площади звезды
и заданной площади звезды 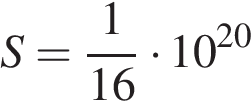 :
:
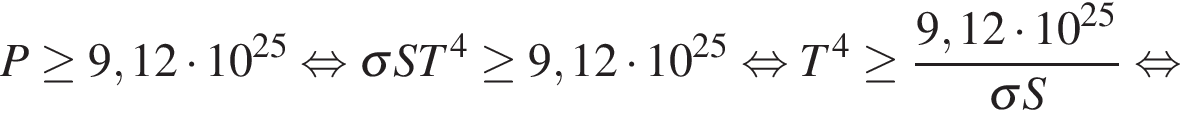
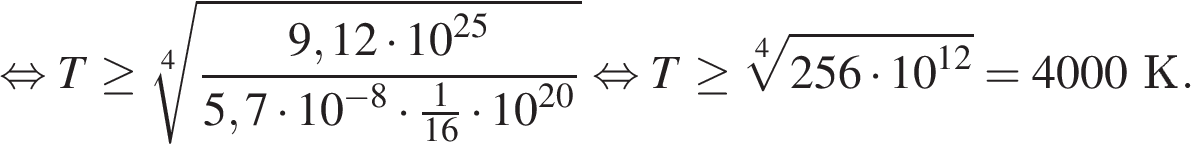
Ответ: 4000.
Ответ: 4000
10. B 12. Опорные башмаки шагающего экскаватора, имеющего массу 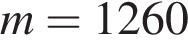 тонн, представляют собой две пустотелые балки длиной
тонн, представляют собой две пустотелые балки длиной 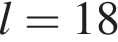 метров и шириной
метров и шириной 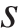 метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой
метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой 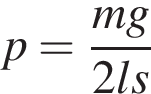 , где
, где  – масса экскаватора (в тоннах),
– масса экскаватора (в тоннах),  – длина балок в метрах,
– длина балок в метрах, 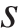 – ширина балок в метрах,
– ширина балок в метрах, 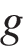 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  м/с
м/с  ). Определите наименьшую возможную ширину опорных балок, если известно, что давление
). Определите наименьшую возможную ширину опорных балок, если известно, что давление 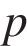 не должно превышать 140 кПа. Ответ выразите в метрах.
не должно превышать 140 кПа. Ответ выразите в метрах.
Вариант № 3711860
1. B 12. Плоский замкнутый контур площадью 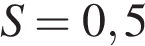 м
м  находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой
находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой  , где
, где  – острый угол между направлением магнитного поля и перпендикуляром к контуру,
– острый угол между направлением магнитного поля и перпендикуляром к контуру,  Тл/с – постоянная,
Тл/с – постоянная, 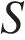 – площадь замкнутого контура, находящегося в магнитном поле (в м
– площадь замкнутого контура, находящегося в магнитном поле (в м  ). При каком минимальном угле
). При каком минимальном угле  (в градусах) ЭДС индукции не будет превышать
(в градусах) ЭДС индукции не будет превышать  В?
В?
Решение.
Задача сводится к решению неравенства 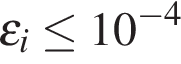 на интервале
на интервале  при заданных значениях площади контура
при заданных значениях площади контура  и постоянной
и постоянной 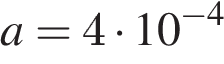 Тл/с:
Тл/с:
 .
.
Ответ: 60.
Ответ: 60
2. B 12. Скорость колеблющегося на пружине груза меняется по закону  (см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
(см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Решение.
Задача сводится к решению неравенства 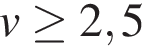 cм/с при заданном законе изменения скорости
cм/с при заданном законе изменения скорости  :
:

Таким образом, 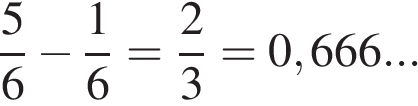 первой секунды после начала движения скорость груза превышала 2,5 см/с. Округляя, получаем 0,67.
первой секунды после начала движения скорость груза превышала 2,5 см/с. Округляя, получаем 0,67.
Ответ: 0,67.
Ответ: 0,67
3. B 12. Сила тока в цепи 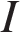 (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:
(в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 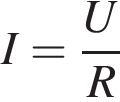 , где
, где 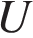 – напряжение в вольтах,
– напряжение в вольтах,  – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
– сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
Решение.
Задача сводится к решению неравенства  А при известном значении напряжения
А при известном значении напряжения  В:
В:
 Ом.
Ом.
Ответ: 55.
Ответ: 55
4. B 12. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности 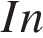 , оперативности
, оперативности  , объективности публикаций
, объективности публикаций  , а также качества сайта
, а также качества сайта 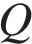 . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2.
. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2.
Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
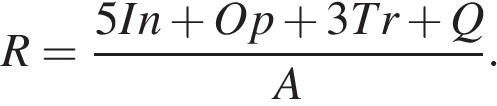
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число  , при котором это условие будет выполняться.
, при котором это условие будет выполняться.
Решение.
Обозначим совпадающую оценку по разным показателям 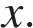 Поскольку все показатели равны друг другу, все они равны
Поскольку все показатели равны друг другу, все они равны 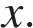 Подставим значения в формулу, учитывая, что рейтинг равен
Подставим значения в формулу, учитывая, что рейтинг равен 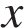 :
:

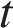 , прошедшее от момента начала торможения, автомобиль проедет 30 метров:
, прошедшее от момента начала торможения, автомобиль проедет 30 метров:
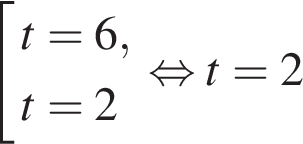 .
.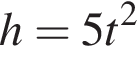 , где
, где  – расстояние в метрах,
– расстояние в метрах, 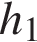 – расстояние до воды до дождя,
– расстояние до воды до дождя,  – расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным
– расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным 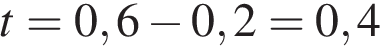 с. Уровень воды поднимется на
с. Уровень воды поднимется на  метров.
метров.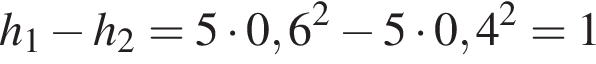
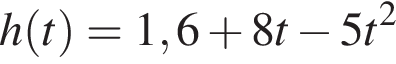 , где
, где  :
: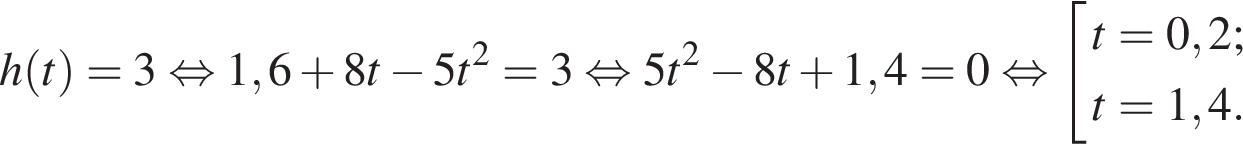
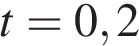 (с) мяч находился на высоте 3 метра, двигаясь снизу вверх, а в момент времени
(с) мяч находился на высоте 3 метра, двигаясь снизу вверх, а в момент времени 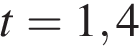 (с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее трёх метров 1,2 секунды.
(с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее трёх метров 1,2 секунды. км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением
км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 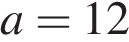 км/ч
км/ч  . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением
. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 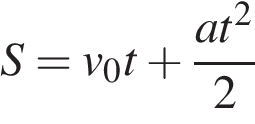 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.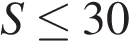 км. Задача сводится к нахождению наибольшего решения неравенства
км. Задача сводится к нахождению наибольшего решения неравенства  и
и 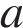 :
:
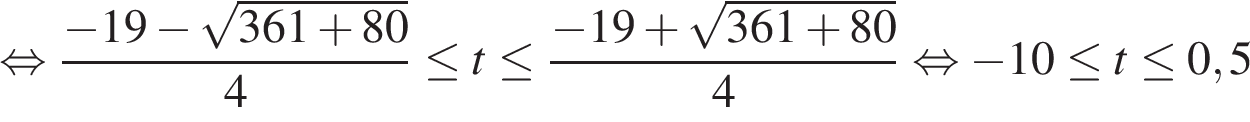
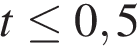 ч, то есть
ч, то есть 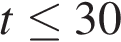 мин.
мин. км с постоянным ускорением
км с постоянным ускорением  . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2. , где
, где  (Па) — давление в газе,
(Па) — давление в газе, 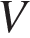 — объeм газа в кубических метрах,
— объeм газа в кубических метрах, 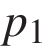 и
и  – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства
– конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства 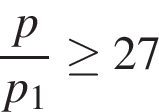 , причем
, причем 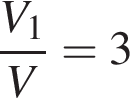 :
: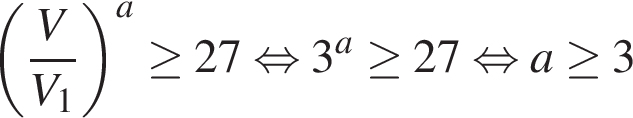 .
. (см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
(см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.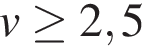 cм/с при заданном законе изменения скорости
cм/с при заданном законе изменения скорости 
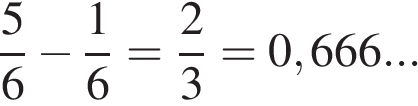 первой секунды после начала движения скорость груза превышала 2,5 см/с. Округляя, получаем 0,67.
первой секунды после начала движения скорость груза превышала 2,5 см/с. Округляя, получаем 0,67. м/с под острым углом
м/с под острым углом  к рельсам. От толчка платформа начинает ехать со скоростью
к рельсам. От толчка платформа начинает ехать со скоростью  (м/с), где
(м/с), где  кг – масса скейтбордиста со скейтом, а
кг – масса скейтбордиста со скейтом, а  кг – масса платформы. Под каким максимальным углом
кг – масса платформы. Под каким максимальным углом 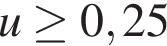 на интервале
на интервале  при заданных значениях массы скейтбордиста
при заданных значениях массы скейтбордиста 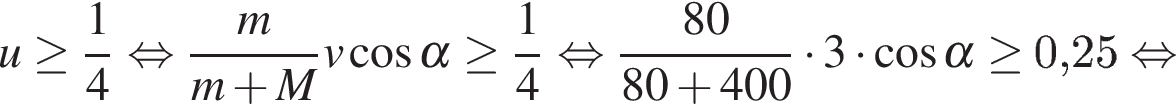
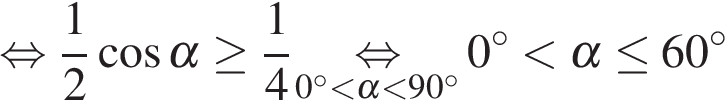 .
.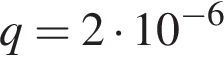 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет
Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет  м/с, на него начинает действовать постоянное магнитное поле, вектор индукции
м/с, на него начинает действовать постоянное магнитное поле, вектор индукции  которого лежит в той же плоскости и составляет угол
которого лежит в той же плоскости и составляет угол  Тл. При этом на шарик действует сила Лоренца, равная
Тл. При этом на шарик действует сила Лоренца, равная  (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла
(Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла  шарик оторвeтся от поверхности, если для этого нужно, чтобы сила
шарик оторвeтся от поверхности, если для этого нужно, чтобы сила  была не менее чем
была не менее чем 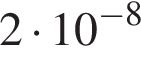 Н? Ответ дайте в градусах.
Н? Ответ дайте в градусах.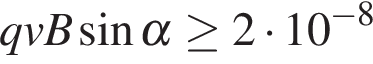 на интервале
на интервале 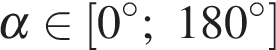 при заданных значениях заряда шарика
при заданных значениях заряда шарика 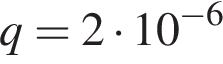 Кл, индукции магнитного поля
Кл, индукции магнитного поля 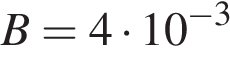 Тл и скорости
Тл и скорости 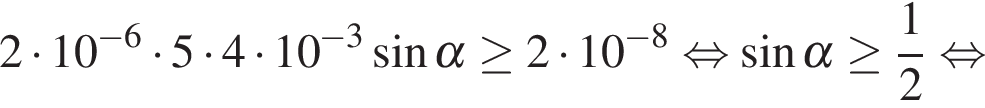
 .
.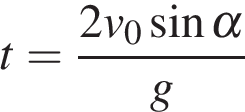 . При каком наименьшем значении угла
. При каком наименьшем значении угла  м/с? Считайте, что ускорение свободного падения
м/с? Считайте, что ускорение свободного падения  м/с
м/с  на интервале
на интервале 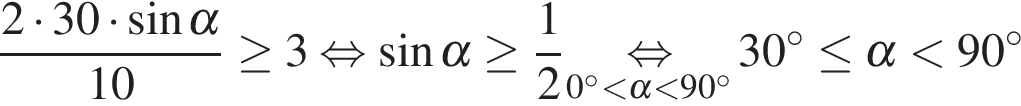 .
. , вычисляется по формуле
, вычисляется по формуле  при известном значении длины пути
при известном значении длины пути 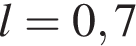 км:
км: км/ч2.
км/ч2. Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление
Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление 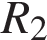 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями
этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями 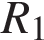 Ом и
Ом и  (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ (в омах.)
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ (в омах.)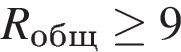 Ом при известном значении сопротивления приборов
Ом при известном значении сопротивления приборов 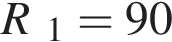 Ом:
Ом: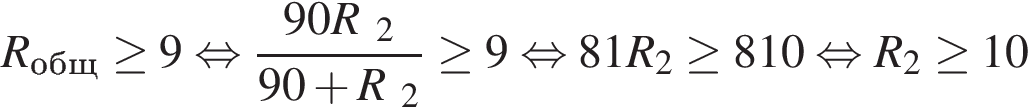 Ом.
Ом. , измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры:
, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры:  , где
, где  – постоянная, площадь
– постоянная, площадь 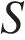 измеряется в квадратных метрах, а температура
измеряется в квадратных метрах, а температура 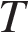 – в градусах Кельвина. Известно, что некоторая звезда имеет площадь
– в градусах Кельвина. Известно, что некоторая звезда имеет площадь  м
м 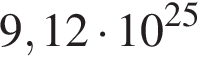 Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.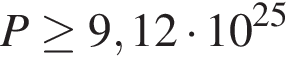 при известном значениях постоянной
при известном значениях постоянной  и заданной площади звезды
и заданной площади звезды 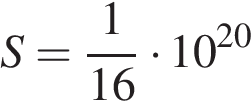 :
: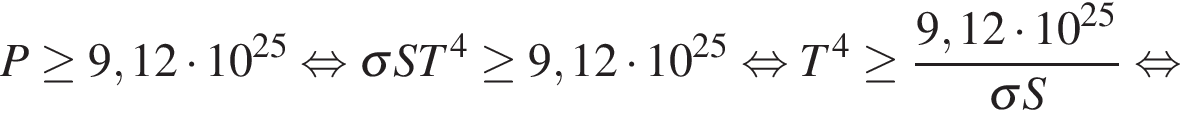
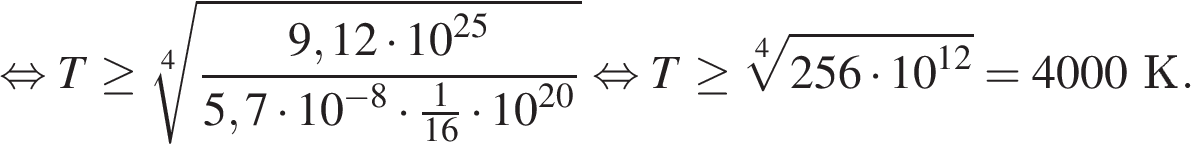
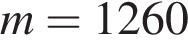 тонн, представляют собой две пустотелые балки длиной
тонн, представляют собой две пустотелые балки длиной 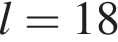 метров и шириной
метров и шириной  метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой
метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой 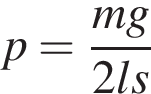 , где
, где  – масса экскаватора (в тоннах),
– масса экскаватора (в тоннах), 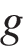 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 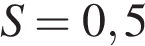 м
м  , где
, где  Тл/с – постоянная,
Тл/с – постоянная,  В?
В?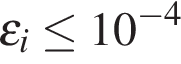 на интервале
на интервале  и постоянной
и постоянной 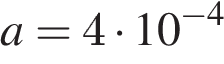 Тл/с:
Тл/с: .
. (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:
(в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 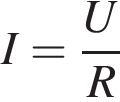 , где
, где 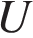 – напряжение в вольтах,
– напряжение в вольтах,  – сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
– сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах. А при известном значении напряжения
А при известном значении напряжения  В:
В: Ом.
Ом.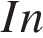 , оперативности
, оперативности  , объективности публикаций
, объективности публикаций  , а также качества сайта
, а также качества сайта 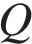 . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2.
. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2.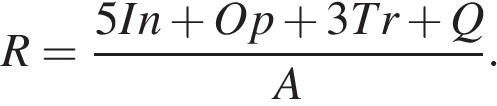
 , при котором это условие будет выполняться.
, при котором это условие будет выполняться.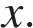 Поскольку все показатели равны друг другу, все они равны
Поскольку все показатели равны друг другу, все они равны 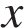 :
:


