Решение. 4 страница
Решение. Отрезок
Ответ: 45. Ответ: 45 8. B 10. Решение. Исходный и отсеченный конус подобны с коэффициентом подобия 2. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площадь отсеченного конуса в 4 раза меньше площади поверхности исходного. Тем самым, она равна 3.
Ответ: 3. Ответ: 3 9. B 10. Решение. Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания
Подставим значения
откуда находим, что Ответ: 12. Ответ: 12 10. B 10. Решение. Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:
Ответ: 110. Ответ: 110 Вариант № 3706806 1. B 10. Решение. Объем параллелепипеда равен
где
Ответ: 1,5. Ответ: 1,5 2. B 10. Решение. высота цилиндра равна
Ответ: 3. Ответ: 3 3. B 10. Решение. Объем данного многогранника равен разности объемов исходного тетраэдра
Ответ: 0,95. Ответ: 0,95 4. B 10. Решение. В правильной пирамиде вершина проецируется в центр основания, следовательно
Ответ: 17. Ответ: 17 5. B 10. Решение. Найдем площадь грани
Отрезок
Ответ: 4. Ответ: 4 6. B 10.
Решение. Площадь боковой поверхности цилиндра равна произведению длины окружности, лежащей в основании, на высоту. Поэтому высота цилиндра равна 2. Ответ: 2 7. B 10. Решение. Объем данного многогранника равен сумме объемов параллелепипедов со сторонами (5, 3, 3), (6, 3, 3) и (1, 3, 5):
Ответ: 114. Ответ: 114 8. B 10. Решение. Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух квадратов со стороной 1:
Ответ: 92. Ответ: 92 9. B 10. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен Решение.
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем:
Радиус сферы равен
Ответ:56. Ответ: 56 10. B 10. Решение. образующая конуса по теореме Пифагора равна
Ответ: 13. Ответ: 13 Вариант № 3706865 1. B 10. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части. Решение. Объем призмы больше объема пирамиды с такой же площадью основания и высотой в 3 раза. Объем оставшейся части составляет тогда две трети исходного, он равен 4.
Ответ: 4. Ответ: 4 2. B 10. Решение. Отрезок SL является медианой правильного треугольника SAC, а значит, и его высотой. Боковые грани пирамиды равны, поэтому
Ответ: 45. Ответ: 45 3. B 10. Решение. Площадь поверхности тетраэдра равна сумме площадей его граней, которые равны
Ответ: 4. Ответ: 4 4. B 10. Решение. Объем призмы равен произведению площади ее основания на высоту и выражается через сторону основания а и высоту Н формулой
Ответ: 5. Ответ: 5 5.B 10. Решение.
Ответ: 60. Ответ: 60 6. B 10. В правильной треугольной призме Решение.
Отрезки A 1 A и BB 1 лежат на параллельных прямых, поэтому искомый угол между прямыми A 1 A и BB 1 равен углу между прямыми BB 1 и BC 1. Боковая грань CBB 1 C 1 — квадрат, поэтому угол между его стороной и диагональю равен 45°.
Ответ: 45. Ответ: 45 7. B 10.
Решение.
Ответ: 4. Ответ: 4 8. B 10. Решение. Объем данного многогранника равен разнице объемов параллелепипедов со сторонами 5, 5, 4 и 1, 2, 5:
Ответ: 90. Ответ: 90 9. B 10. Решение. образующая конуса по теореме Пифагора равна
Ответ: 17. Ответ: 17 10. B 10. Решение. Объем данного многогранника равен разности объемов исходного тетраэдра
Ответ: 0,95. Ответ: 0,95 Вариант № 3706913 1. B 10. Решение. Объем данного многогранника равен разности объемов параллелепипедов со сторонами 4, 4, 5 и 1, 2, 1:
Ответ: 78. Ответ: 78 2. B 10. Решение. Объем параллелепипеда равен
Ответ: 2. Ответ: 2 3. B 10. Решение. Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
Ответ: 216. Ответ: 216 4. B 10.
Решение.
Ответ: 6. Ответ: 6 5. B 10. В правильной треугольной пирамиде Решение.
Ответ: 3. Ответ: 3 6. B 10. Решение.
Ответ: 6.
Ответ: 6 7. B 10. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины. Решение. Поскольку высота куба равна высоте призмы, их объемы пропорциональны площадям их оснований. Площадь основания построенной призмы в 8 раз меньше площади основания исходной, поэтому искомый объем призмы равен 12: 8 = 1,5.
Ответ: 1,5. Ответ: 1,5 8. B 10. Решение. Радиус большого круга является радиусом шара. Площадь первого выражается через радиус
Ответ: 12. Ответ: 12 9. B 10. Решение. По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 1/2 исходного объема, поэтому объем детали равен 3 литрам. Ответ: 3. Ответ: 3 10. B 10. Решение. Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:
Ответ: 96. Ответ: 96 Вариант № 3706937 1. B 10. В правильной четырёхугольной призме Решение.
Правильная четырёхугольная призма является прямоугольным параллелепипедом, диагонали прямоугольного параллелепипеда равны, диагональное сечение является прямоугольником.
Рассмотрим прямоугольный треугольник A 1 BC: в нем катет BC вдвое меньше гипотенузы A 1 C, поэтому угол A 1 CB равен 60°. Аналогично в треугольнике D 1 CB угол D 1 BC равен 60°.
Сумма углов треугольника BGC равна 180° получаем, поскольку углы два его угла равны 60°, третий угол тоже равен 60°.
Ответ: 60. Ответ: 60
|

 является медианой равнобедренного треугольника
является медианой равнобедренного треугольника  , а значит, и его высотой. Тогда
, а значит, и его высотой. Тогда
 Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760. и боковое ребро
и боковое ребро  как
как
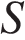 :
: ,
,
 Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Объем параллелепипеда
Объем параллелепипеда  равен 9. Найдите объем треугольной пирамиды
равен 9. Найдите объем треугольной пирамиды  .
. , где
, где  – высота. Объем пирамиды равен
– высота. Объем пирамиды равен ,
, – площадь основания пирамиды, по построению равная половине площади основания параллелепипеда. Тогда объем пирамиды в 6 раз меньше объема параллелепипеда.
– площадь основания пирамиды, по построению равная половине площади основания параллелепипеда. Тогда объем пирамиды в 6 раз меньше объема параллелепипеда. Площадь боковой поверхности цилиндра равна 21
Площадь боковой поверхности цилиндра равна 21  , а диаметр основания равен 7. Найдите высоту цилиндра.
, а диаметр основания равен 7. Найдите высоту цилиндра.
 Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра. и четырех тетраэдров, одни из вершин которых совпадают с вершинами исходного:
и четырех тетраэдров, одни из вершин которых совпадают с вершинами исходного: .
. В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде  точка
точка  – центр основания,
– центр основания,  ,
,  . Найдите боковое ребро
. Найдите боковое ребро  .
. является высотой пирамиды. тогда по теореме Пифагора
является высотой пирамиды. тогда по теореме Пифагора
 В правильной треугольной пирамиде
В правильной треугольной пирамиде 
 – середина ребра
– середина ребра  ,
,  =7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка
=7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка  .
.

 Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). .
. . Найдите образующую конуса.
. Найдите образующую конуса.

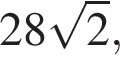 поэтому образующая равна
поэтому образующая равна 
 Высота конуса равна 12, а диаметр основания – 10. Найдите образующую конуса.
Высота конуса равна 12, а диаметр основания – 10. Найдите образующую конуса.
 В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
 Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза? . Поэтому при увеличении ребер вдвое, площадь поверхности увеличится в 4 раза.
. Поэтому при увеличении ребер вдвое, площадь поверхности увеличится в 4 раза. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см. . Поэтому
. Поэтому  , а значит, при увеличении стороны а в 4 раза знаменатель увеличится в 16 раз, то есть высота уменьшится в 16 раз и будет равна 5 см.
, а значит, при увеличении стороны а в 4 раза знаменатель увеличится в 16 раз, то есть высота уменьшится в 16 раз и будет равна 5 см. Найдите угол
Найдите угол  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.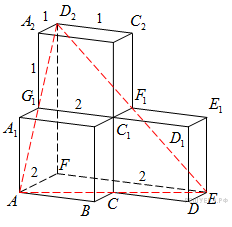 Рассмотрим треугольник
Рассмотрим треугольник  , т. к. это диагонали равных квадратов. Таким образом, треугольник
, т. к. это диагонали равных квадратов. Таким образом, треугольник  .
. , все ребра которой равны 3, найдите угол между прямыми
, все ребра которой равны 3, найдите угол между прямыми  и
и  . Ответ дайте в градусах.
. Ответ дайте в градусах.
 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
, 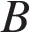 ,
,  ,
,  ,
,  ,
, 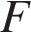 ,
,  правильной шестиугольной призмы
правильной шестиугольной призмы  , площадь основания которой равна 4, а боковое ребро равно 3.
, площадь основания которой равна 4, а боковое ребро равно 3. Основание пирамиды такое же, как основание правильной шестиугольной призмы, и высота у них общая. Поэтому
Основание пирамиды такое же, как основание правильной шестиугольной призмы, и высота у них общая. Поэтому
 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). .
.
 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Объем параллелепипеда
Объем параллелепипеда  .
. а объем пирамиды равен
а объем пирамиды равен  . Высота пирамиды равна высоте параллелепипеда, а ее основание вдвое меньше, поэтому
. Высота пирамиды равна высоте параллелепипеда, а ее основание вдвое меньше, поэтому
 В куб вписан шар радиуса 3. Найдите объем куба.
В куб вписан шар радиуса 3. Найдите объем куба. .
. ,
,  ,
,  правильной шестиугольной призмы
правильной шестиугольной призмы  Площадь основания четырехугольной призмы равна половине площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому
Площадь основания четырехугольной призмы равна половине площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому .
. . Объем пирамиды равен
. Объем пирамиды равен  ,
,  . Найдите площадь треугольника
. Найдите площадь треугольника 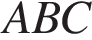 .
. Основание пирамиды — равносторонний треугольник, поэтому,
Основание пирамиды — равносторонний треугольник, поэтому,  . Тогда
. Тогда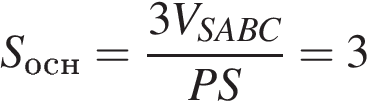 .
. Найдите квадрат расстояния между вершинами
Найдите квадрат расстояния между вершинами  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. По теореме Пифагора
По теореме Пифагора
 Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Площадь большого круга шара равна 3. Найдите площадь поверхности шара. как
как  , а площадь поверхности сферы – как
, а площадь поверхности сферы – как  . Видно, что площадь поверхности шара в
. Видно, что площадь поверхности шара в  раза больше площади поверхности большого круга.
раза больше площади поверхности большого круга. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
 . Найдите угол между диагоналями
. Найдите угол между диагоналями  и
и  . Ответ дайте в градусах.
. Ответ дайте в градусах.



