Решение. 1 страница
Topic B: Maternal and Child Undernutrition in Less Developed Countries (LDCs) Undernutrition contributes to more than one 3rd of all deaths in children under the age of 5. It does this by stealing children’s strength. An undernourished child struggles to withstand an attack of pneumonia, diarrhea or other illness – and illness often prevails.
The 1st Millennium Development Goal calls for the eradication of extreme poverty and hunger, and its achievement is crucial for national progress and development. For instance, goal that is about achieving universal primary education can never be achieved if children are not adequately nourished and can attend school. At present, many of the world’s less development countries and most of the world’s less development countries and most of the world’s poorest nations are not on track to achieve some of the MDGs.
The Republic of Guinea-Bissau is a country in West Africa with an estimated population of 1,600,000. Guinea-Bissau’s Human Development Index is one of the lowest on earth. More than 2/3 of the population lives under the poverty line. The economy depends mainly on agriculture; fish, cashew nuts and ground nuts are its major exports.
Life expectancy at birth has climbed since 1990, but remains short: life expectancy for a child born in 2008 was 49 years (and only 47 years for a boy). 1 out of 18 pregnant women die as a result of pregnancy. According to a 2013 UNICEF report, 50% of women in Guinea-Bissau had undergone female genital mutilation. In 2010, Guinea-Bissau had the 7th highest maternal mortality rate in the world.
These statistics are familiar to African and Asian countries too. In order to halve the proportion of hungry people around the world Guinea-Bissau urges: - To help women gain equal access to life’s basic necessity - To work out school feeding programs - To repair irrigation systems - To improve access to food for the most vulnerable and food-insecure people
Where undernutrition is widespread, negative consequences for individuals translate into negative consequences for countries. Knowing whether children are at risk of nutritional deficiencies, and taking appropriate actions to prevent and treat such deficiencies, is therefore imperative. With more than 1 billion people suffering from malnutrition and hunger, international leadership and urgent action are needed. Guinea-Bissau seeks friendly and cooperative relations and calls for worldwide engagement in maternal and child undernutrition obviation. Вариант № 3701178 1. B 10. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Решение.
Ответ: 6. Ответ: 6 2. B 10. Решение.
Тогда длина ребра равна
Ответ: 3. Ответ: 3 3. B 10. Решение. грань Ответ: 45. Ответ: 45 4. B 10. Решение.
Ответ: 60. Ответ: 60 5. B 10.
Решение.
Ответ: 8. Ответ: 8 6. B 10.
Решение.
Ответ: 6. Ответ: 6 7.B 10. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы. Решение. Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Тогда длина его ребра
Радиус сферы равен половине длины ребра Ответ: 3. Ответ: 3 8.B 10. Решение.
Ответ: 45. Ответ: 45 9. B 10. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра. Решение.
Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара (см. рис.).
Площадь основания цилиндра:
Площадь боковой поверхности цилиндра:
Площадь полной поверхности цилиндра:
Поскольку площадь поверхности шара дается формулой
Ответ:166,5. Ответ: 166,5 B 10. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Вариант № 3701195 1. B 10. Решение. Площадь боковой поверхности цилиндра Ответ: 12. Ответ: 12 2. B 10. Решение. Рассмотрим прямоугольник
Значит, AD
Ответ: 5. Ответ: 5 3. B 10. Решение. Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
Ответ: 216. Ответ: 216 4. B 10. Решение. Площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4, уменьшенной на две площади прямоугольников со сторонами 3 и 4:
Ответ: 162. Ответ: 162 5. B 10. Решение. площадь боковой поверхности фигуры равна сумме площадей всех боковых граней
Ответ: 300. Ответ: 300 6. B 10. Решение. Объем данного многогранника равен сумме объемов параллелепипедов со сторонами 2, 3, 2 и 1, 3, 4:
Ответ: 24. Ответ: 24 7. B 10. Решение. образующая конуса по теореме Пифагора равна
Ответ: 17. Ответ: 17 8. B 10. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины. Решение. Поскольку высота куба равна высоте призмы, их объемы пропорциональны площадям их оснований. Площадь основания построенной призмы в 8 раз меньше площади основания исходной, поэтому искомый объем призмы равен 12: 8 = 1,5.
Ответ: 1,5. Ответ: 1,5 9. B 10. Решение. Площадь поверхности тела равна сумме поверхностей трех составляющих ее параллелепипедов с ребрами 2, 3, 5; 1, 3, 5 и 2, 2, 3:
Ответ: 140. Ответ: 140 10. B 10. Решение.
Ответ: 11.
Ответ: 11
Вариант № 3701239 1. B 10. Решение. Если ребро куба равно
Тогда диагональ равна 6. Ответ: 6. Ответ: 6 2. B 10. Решение. Рассмотрим прямоугольный треугольник
В прямоугольнике
Ответ: 50. Ответ: 50 3. B 10. Решение. грань Ответ: 45. Ответ: 45 4. B 10. Решение. По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 9/12 исходного объема:
Ответ: 1500. Ответ: 1500 5. B 10. Решение. образующая конуса по теореме Пифагора равна
Ответ: 17. Ответ: 17 6. B 10. Решение. Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
Ответ: 8. Ответ: 8 7. B 10. Решение. Объем пирамиды равен
Ответ: 2.
Примечание. Куб состоит из 6 таких пирамид, объем каждой из них равен 2. Ответ: 2 8. B 10. В сосуде, имеющем форму конуса, уровень жидкости достигает
Решение. Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости.
Ответ: 490. Ответ: 490 9. B 10. Решение.
Ответ: 11.
Ответ: 11 10. B 10.
Решение.
Ответ: 6. Ответ: 6 Вариант № 3704952 1. B 10. Решение. высота цилиндра равна
Ответ: 3. Ответ: 3 2. B 10.
|

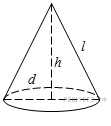 Радиус основания конуса, его высота и образующая связаны соотношением
Радиус основания конуса, его высота и образующая связаны соотношением  . В нашем случае
. В нашем случае  , поэтому
, поэтому  . Следовательно, диаметр основания конуса равен 6.
. Следовательно, диаметр основания конуса равен 6.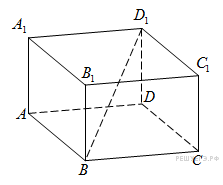 В прямоугольном параллелепипеде
В прямоугольном параллелепипеде  известно, что
известно, что 

 Найдите длину ребра
Найдите длину ребра  .
.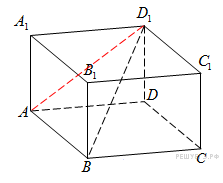 По теореме Пифагора
По теореме Пифагора

 Найдите угол
Найдите угол  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого  =4,
=4,  =4. Дайте ответ в градусах.
=4. Дайте ответ в градусах. является квадратом со стороной 4, а
является квадратом со стороной 4, а  – диагональ этой грани, значит, угол
– диагональ этой грани, значит, угол 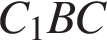 равен
равен 
 Найдите угол
Найдите угол  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Рассмотрим треугольник
Рассмотрим треугольник  где
где  т. к. являются диагоналями равных квадратов. Следовательно, треугольник
т. к. являются диагоналями равных квадратов. Следовательно, треугольник 
 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
, 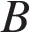 ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  , у которого
, у которого  ,
,  ,
, 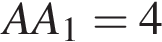 .
. Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому
Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому
 ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  ,
,  Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому
Площадь основания пирамиды в два раза меньше площади основания пареллелепипеда, а высота у них общая. Поэтому

 .
. Найдите угол
Найдите угол  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
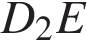 – диагональ квадрата со стороной 2, значит, треугольник
– диагональ квадрата со стороной 2, значит, треугольник  .
.



 имеем:
имеем: 
 Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на  .
. , поэтому
, поэтому 
 Найдите расстояние между вершинами А и D
Найдите расстояние между вершинами А и D  прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA
прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA  в котором
в котором  является диагональю,
является диагональю,  =
=  По теореме Пифагора
По теореме Пифагора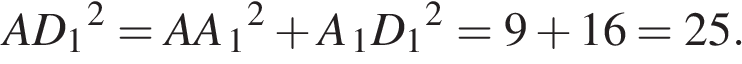
 В куб вписан шар радиуса 3. Найдите объем куба.
В куб вписан шар радиуса 3. Найдите объем куба. .
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10. .
. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.
Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса.
 Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

 .
. Найдите квадрат расстояния между вершинами
Найдите квадрат расстояния между вершинами  и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. рассмотрим прямоугольный треугольник
рассмотрим прямоугольный треугольник  По теореме Пифагора
По теореме Пифагора
 Объем куба равен
Объем куба равен  . Найдите его диагональ.
. Найдите его диагональ. , то его объем и диагональ даются формулами
, то его объем и диагональ даются формулами  и
и  Следовательно,
Следовательно,
 Найдите квадрат расстояния между вершинами C и A 1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA 1=3.
Найдите квадрат расстояния между вершинами C и A 1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA 1=3. в котором
в котором  является гипотенузой. По теореме Пифагора
является гипотенузой. По теореме Пифагора

 – диагональ,
– диагональ,  . Значит,
. Значит,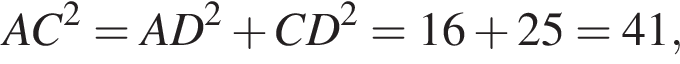

 В цилиндрический сосуд налили 2000
В цилиндрический сосуд налили 2000  воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в  .
.
 В куб вписан шар радиуса 1. Найдите объем куба.
В куб вписан шар радиуса 1. Найдите объем куба. .
. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба. .
. высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
 Площадь боковой поверхности цилиндра равна 9
Площадь боковой поверхности цилиндра равна 9 
 В правильной треугольной пирамиде
В правильной треугольной пирамиде 
 – середина ребра
– середина ребра 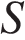 – вершина. Известно, что
– вершина. Известно, что  =7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка
=7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка  .
.


