Решение.
Объем шара радиуса  равен
равен
 .
.
При увеличении радиуса втрое, объем шара увеличится в 27 раз.
Ответ: 27.
Ответ: 27
5. B 10.  Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Решение.
Объем куба с ребром  равен
равен  . Увеличение объема равно 19:
. Увеличение объема равно 19:

Решим уравнение:

Тем самым,  .
.
Ответ: 2.
Ответ: 2
6. B 10.  В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Решение.
Отрезок SL является медианой правильного треугольника SAC, а значит, и его высотой. Боковые грани пирамиды равны, поэтому

Ответ: 45.
Ответ: 45
7. B 10.  Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Решение.
При увеличении ребер в 3 раза площади треугольников, образующих грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности также увеличится в 9 раз.
Ответ: 9.
Ответ: 9
8. B 10.  Найдите угол
Найдите угол  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого  =5,
=5,  =4,
=4,  =4. Дайте ответ в градусах.
=4. Дайте ответ в градусах.
Решение.
грань  является квадратом со стороной 4, а
является квадратом со стороной 4, а  – диагональ этой грани, значит, угол
– диагональ этой грани, значит, угол 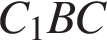 равен
равен 
Ответ: 45.
Ответ: 45
9. B 10.  Высота конуса равна 6, а диаметр основания – 16. Найдите образующую конуса.
Высота конуса равна 6, а диаметр основания – 16. Найдите образующую конуса.
Решение.
образующая конуса по теореме Пифагора равна

Ответ: 10.
Ответ: 10
10. B 10. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Решение.
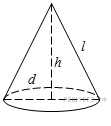 Радиус основания конуса, его высота и образующая связаны соотношением
Радиус основания конуса, его высота и образующая связаны соотношением  . В нашем случае
. В нашем случае  , поэтому
, поэтому  . Следовательно, диаметр основания конуса равен 6.
. Следовательно, диаметр основания конуса равен 6.
Ответ: 6.
Ответ: 6
Вариант № 3706631
1. B 10.  Площадь боковой поверхности цилиндра равна 21
Площадь боковой поверхности цилиндра равна 21  , а диаметр основания равен 7. Найдите высоту цилиндра.
, а диаметр основания равен 7. Найдите высоту цилиндра.
Решение.
высота цилиндра равна

Ответ: 3.
Ответ: 3
2. B 10.  Найдите тангенс угла
Найдите тангенс угла  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Решение.
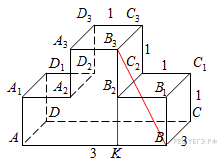
Опустим перпендикуляр  из точки
из точки  на отрезок
на отрезок  . Угол
. Угол  равен углу
равен углу  . В прямоугольном треугольнике
. В прямоугольном треугольнике  имеем:
имеем:

Ответ: 2.
Ответ: 2
3. B 10. 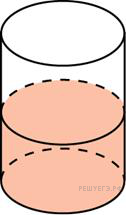 В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Решение.
По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 1/2 исходного объема, поэтому объем детали равен 3 литрам.
Ответ: 3.
Ответ: 3
4. B 10.  Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение.
Площадь поверхности заданного многогранника складывается из четырех площадей квадратов со стороной 1, двух прямоугольников со сторонами 1 и 2 и двух граней (передней и задней), площади которых в свою очередь складываются из трех единичных квадратов каждая. Всего 4 + 4 + 6 = 14.
Ответ: 14.
Ответ: 14
5. B 10.  Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Решение.
Площадь поверхности шара выражается через его радиус формулой  , поэтому при увеличении радиуса вдвое площадь увеличится в 22 = 4 раза.
, поэтому при увеличении радиуса вдвое площадь увеличится в 22 = 4 раза.
Ответ: 4.
Ответ: 4
6. B 10. 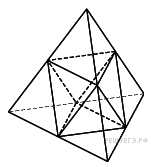 Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.
Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.
Решение.
Искомая поверхность состоит из 8 равносторонних треугольников со стороной, вдвое меньшей ребра исходного тетраэдра. Поверхность исходного тетраэдра состоит из 16-ти таких треугольников (см. рис.), поэтому искомая площадь равна половине площади поверхности тетраэдра и равна 0,6.
Ответ: 0,6.
Ответ: 0,6
7. B 10.  В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде  точка
точка  – центр основания,
– центр основания, 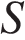 – вершина,
– вершина,  ,
,  . Найдите боковое ребро
. Найдите боковое ребро  .
.
Решение.
в правильной пирамиде вершина проецируется в центр основания, следовательно  является высотой пирамиды. тогда по теореме Пифагора
является высотой пирамиды. тогда по теореме Пифагора

Ответ: 17.
Ответ: 17
8. B 10. В правильной треугольной пирамиде 
 — середина ребра
— середина ребра  ,
, 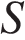 — вершина. Известно, что
— вершина. Известно, что  , а площадь боковой поверхности равна
, а площадь боковой поверхности равна  . Найдите длину отрезка
. Найдите длину отрезка  .
.
Решение.
 Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему:
Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему:  . Тогда
. Тогда  .
.
Ответ: 2
9. B 10.  Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:
 .
.
Ответ: 110.
Ответ: 110
10. B 10. 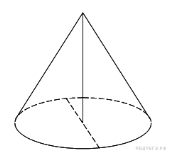 Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Решение.
образующая конуса по теореме Пифагора равна

Ответ: 17.
Ответ: 17
Вариант № 3706686
1. B 10.  Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5 и площади двух квадратов со стороной 1:
 .
.
Ответ: 92.
Ответ: 92
2. B 10.  В правильной треугольной пирамиде
В правильной треугольной пирамиде 
 – середина ребра
– середина ребра  ,
, 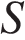 – вершина. Известно, что
– вершина. Известно, что  =5, а
=5, а  =6. Найдите площадь боковой поверхности пирамиды.
=6. Найдите площадь боковой поверхности пирамиды.
Решение.
Отрезок  является медианой равнобедренного треугольника
является медианой равнобедренного треугольника  , а значит, и его высотой. Тогда
, а значит, и его высотой. Тогда

Ответ: 45.
Ответ: 45
3. B 10.  Найдите квадрат расстояния между вершинами
Найдите квадрат расстояния между вершинами  и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Решение.
 рассмотрим прямоугольный треугольник
рассмотрим прямоугольный треугольник  По теореме Пифагора
По теореме Пифагора

Ответ: 11.
Ответ: 11
4. B 10.  Объем треугольной пирамиды
Объем треугольной пирамиды  , являющейся частью правильной шестиугольной пирамиды
, являющейся частью правильной шестиугольной пирамиды  , равен 1. Найдите объем шестиугольной пирамиды.
, равен 1. Найдите объем шестиугольной пирамиды.
Решение.
Данные пирамиды имеют общую высоту, поэтому их объемы соотносятся как площади их оснований. Площадь правильного шестиугольника со стороной  равна
равна  Площадь же равнобедренного треугольника
Площадь же равнобедренного треугольника  с боковой стороной
с боковой стороной  и углах при основании
и углах при основании  равна
равна  Получаем, что площадь шестиугольника больше площади треугольника
Получаем, что площадь шестиугольника больше площади треугольника  в
в 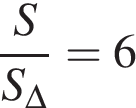 раз и равна 6.
раз и равна 6.
Ответ: 6.
Ответ: 6
5. B 10.  Высота конуса равна 5, а диаметр основания – 24. Найдите образующую конуса.
Высота конуса равна 5, а диаметр основания – 24. Найдите образующую конуса.
Решение.
образующая конуса по теореме Пифагора равна

Ответ: 13.
Ответ: 13
6. B 10.  Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
, 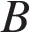 ,
,  правильной треугольной призмы
правильной треугольной призмы  , площадь основания которой равна 4, а боковое ребро равно 3.
, площадь основания которой равна 4, а боковое ребро равно 3.
Решение.

Заметим, что искомый объём равен разности объема призмы и двух треугольных пирамид, основания и высоты которых совпадают с основанием и высотой призмы:

Поэтому

Ответ: 4.
Ответ: 4
7. B 10. В правильной треугольной пирамиде  медианы основания пересекаются в точке
медианы основания пересекаются в точке  . Площадь треугольника
. Площадь треугольника 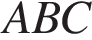 равна 3, объем пирамиды равен 1. Найдите длину отрезка
равна 3, объем пирамиды равен 1. Найдите длину отрезка  .
.
Решение.
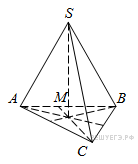 Основание пирамиды — равносторонний треугольник, поэтому, точка
Основание пирамиды — равносторонний треугольник, поэтому, точка  является центром основания, а
является центром основания, а  — высотой пирамиды
— высотой пирамиды  . Ее объем вычисляется по формуле
. Ее объем вычисляется по формуле  . Тогда
. Тогда
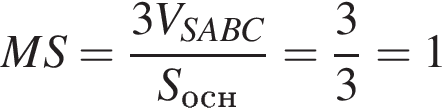 .
.
Ответ: 1.
Ответ: 1
8. B 10. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
Решение.
 Радиус основания конуса, его высота и образующая связаны соотношением
Радиус основания конуса, его высота и образующая связаны соотношением  . В нашем случае
. В нашем случае  , поэтому
, поэтому  . Следовательно, диаметр основания конуса равен 6.
. Следовательно, диаметр основания конуса равен 6.
Ответ: 6.
Ответ: 6
9. B 10.  Площадь боковой поверхности цилиндра равна 9
Площадь боковой поверхности цилиндра равна 9  , а диаметр основания равен 3. Найдите высоту цилиндра.
, а диаметр основания равен 3. Найдите высоту цилиндра.
Решение.
высота цилиндра равна

Ответ: 3.
Ответ: 3
10. B 10. В правильной треугольной пирамиде  медианы основания пересекаются в точке
медианы основания пересекаются в точке  . Площадь треугольника
. Площадь треугольника 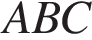 равна
равна  ,
,  . Найдите объем пирамиды
. Найдите объем пирамиды
Вариант № 3706719
1. B 10. Площадь боковой поверхности цилиндра равна  , а высота — 1. Найдите диаметр основания.
, а высота — 1. Найдите диаметр основания.
Решение.
 Площадь боковой поверхности цилиндра находится по формуле:
Площадь боковой поверхности цилиндра находится по формуле:  ,
,
значит,  .
.
Ответ: 2
2. B 10.  Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4:
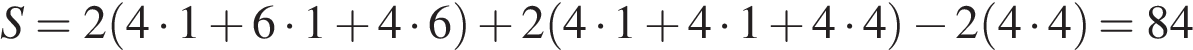 .
.
Ответ: 84.
Приведем другое решение
Площадь поверхности заданного многогранника равна площади прямоугольного параллелепипеда с ребрами 6, 4, 2 уменьшенной на 4 площади квадратов со стороной 1:
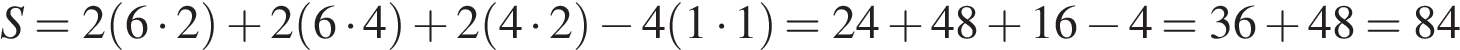
Ответ: 84
3. B 10.  Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  ,
,  прямоугольного параллелепипеда
прямоугольного параллелепипеда  , у которого
, у которого  ,
,  ,
,  .
.
Решение.
 Из рисунка видно, что многогранник является половиной данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника
Из рисунка видно, что многогранник является половиной данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника
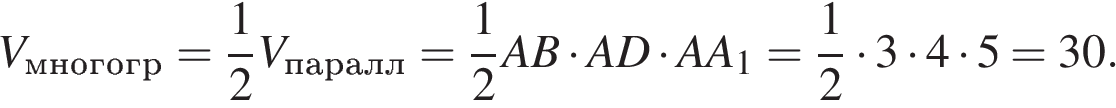
Ответ: 30.
Ответ: 30
4. B 10. В правильной треугольной пирамиде 
 — середина ребра
— середина ребра  ,
,  — вершина. Известно, что
— вершина. Известно, что  , а площадь боковой поверхности равна
, а площадь боковой поверхности равна  . Найдите длину отрезка
. Найдите длину отрезка  .
.
Решение.
 Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему:
Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему:  . Тогда
. Тогда  .
.
Ответ: 2
5. B 10.  Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Решение.
Площадь поверхности куба выражается через его ребро  как
как  , поэтому при увеличении длины ребра на
, поэтому при увеличении длины ребра на  площадь увеличится на
площадь увеличится на

Отсюда находим, что ребро куба равно
 .
.
Ответ: 4.
Ответ: 4
6. B 10.  Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Решение.
Сторона ромба  выражается через его диагонали
выражается через его диагонали  и
и  формулой
формулой
 .
.
Найдем площадь ромба

Тогда площадь поверхности призмы равна

Ответ: 248.
Ответ: 248
7. B 10.  В правильной треугольной пирамиде
В правильной треугольной пирамиде 
 – середина ребра
– середина ребра  ,
, 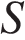 – вершина. Известно, что
– вершина. Известно, что  =5, а
=5, а  =6. Найдите площадь боковой поверхности пирамиды.
=6. Найдите площадь боковой поверхности пирамиды.

 равен
равен .
. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. равен
равен  . Увеличение объема равно 19:
. Увеличение объема равно 19:

 .
. В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
 Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза? Найдите угол
Найдите угол  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого  =5,
=5,  =4,
=4,  =4. Дайте ответ в градусах.
=4. Дайте ответ в градусах. является квадратом со стороной 4, а
является квадратом со стороной 4, а  – диагональ этой грани, значит, угол
– диагональ этой грани, значит, угол 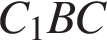 равен
равен 
 Высота конуса равна 6, а диаметр основания – 16. Найдите образующую конуса.
Высота конуса равна 6, а диаметр основания – 16. Найдите образующую конуса.
 Радиус основания конуса, его высота и образующая связаны соотношением
Радиус основания конуса, его высота и образующая связаны соотношением  . В нашем случае
. В нашем случае  , поэтому
, поэтому  . Следовательно, диаметр основания конуса равен 6.
. Следовательно, диаметр основания конуса равен 6. Площадь боковой поверхности цилиндра равна 21
Площадь боковой поверхности цилиндра равна 21  , а диаметр основания равен 7. Найдите высоту цилиндра.
, а диаметр основания равен 7. Найдите высоту цилиндра.
 Найдите тангенс угла
Найдите тангенс угла  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
 из точки
из точки  на отрезок
на отрезок  . В прямоугольном треугольнике
. В прямоугольном треугольнике  имеем:
имеем:
 В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? , поэтому при увеличении радиуса вдвое площадь увеличится в 22 = 4 раза.
, поэтому при увеличении радиуса вдвое площадь увеличится в 22 = 4 раза. Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра.
Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра. В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде  точка
точка  – центр основания,
– центр основания, 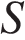 – вершина,
– вершина,  ,
,  . Найдите боковое ребро
. Найдите боковое ребро  .
. является высотой пирамиды. тогда по теореме Пифагора
является высотой пирамиды. тогда по теореме Пифагора

 — середина ребра
— середина ребра  ,
,  , а площадь боковой поверхности равна
, а площадь боковой поверхности равна  . Найдите длину отрезка
. Найдите длину отрезка  .
. Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему:
Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему:  . Тогда
. Тогда  .
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
Высота конуса равна 8, а диаметр основания — 30. Найдите образующую конуса.
 Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). .
. В правильной треугольной пирамиде
В правильной треугольной пирамиде  – середина ребра
– середина ребра  =6. Найдите площадь боковой поверхности пирамиды.
=6. Найдите площадь боковой поверхности пирамиды. , а значит, и его высотой. Тогда
, а значит, и его высотой. Тогда
 Найдите квадрат расстояния между вершинами
Найдите квадрат расстояния между вершинами  и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. рассмотрим прямоугольный треугольник
рассмотрим прямоугольный треугольник  По теореме Пифагора
По теореме Пифагора
 Объем треугольной пирамиды
Объем треугольной пирамиды  , равен 1. Найдите объем шестиугольной пирамиды.
, равен 1. Найдите объем шестиугольной пирамиды. Площадь же равнобедренного треугольника
Площадь же равнобедренного треугольника  с боковой стороной
с боковой стороной  равна
равна  Получаем, что площадь шестиугольника больше площади треугольника
Получаем, что площадь шестиугольника больше площади треугольника 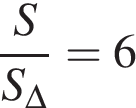 раз и равна 6.
раз и равна 6.
 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
, 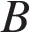 ,
,  правильной треугольной призмы
правильной треугольной призмы  , площадь основания которой равна 4, а боковое ребро равно 3.
, площадь основания которой равна 4, а боковое ребро равно 3.


 . Площадь треугольника
. Площадь треугольника 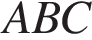 равна 3, объем пирамиды равен 1. Найдите длину отрезка
равна 3, объем пирамиды равен 1. Найдите длину отрезка  .
. Основание пирамиды — равносторонний треугольник, поэтому, точка
Основание пирамиды — равносторонний треугольник, поэтому, точка  . Тогда
. Тогда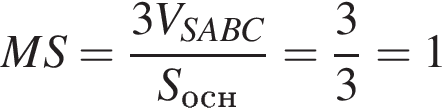 .
.
 . Найдите объем пирамиды
. Найдите объем пирамиды , а высота — 1. Найдите диаметр основания.
, а высота — 1. Найдите диаметр основания. Площадь боковой поверхности цилиндра находится по формуле:
Площадь боковой поверхности цилиндра находится по формуле:  ,
, .
. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).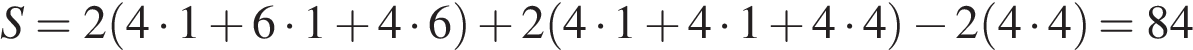 .
.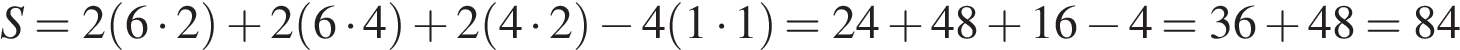
 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  , у которого
, у которого  ,
,  ,
,  .
. Из рисунка видно, что многогранник является половиной данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника
Из рисунка видно, что многогранник является половиной данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника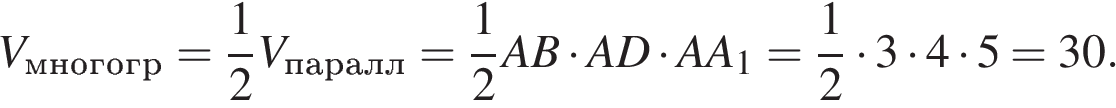
 Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. , поэтому при увеличении длины ребра на
, поэтому при увеличении длины ребра на  площадь увеличится на
площадь увеличится на
 .
. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. и
и  формулой
формулой .
.




