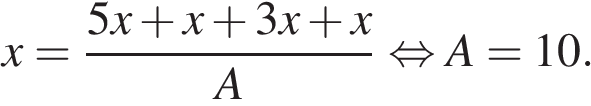
Ответ:10.
Ответ: 10
5. B 12. Мотоциклист, движущийся по городу со скоростью  км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением
км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 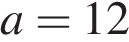 км/ч
км/ч  . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением
. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 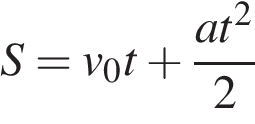 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Решение.
Мотоциклист будет находиться в зоне функционирования сотовой связи, если 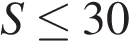 км. Задача сводится к нахождению наибольшего решения неравенства
км. Задача сводится к нахождению наибольшего решения неравенства 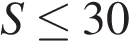 км при заданных значениях параметров
км при заданных значениях параметров  и
и 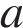 :
:

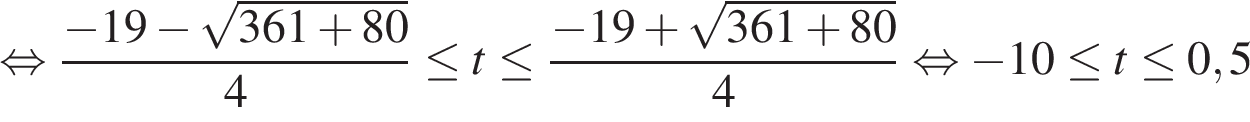
Учитывая то, что время – неотрицательная величина, получаем 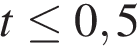 ч, то есть
ч, то есть 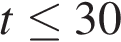 мин.
мин.
Ответ: 30.
Ответ: 30
6. B 12. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:  , где
, где  – длина ребра куба в метрах,
– длина ребра куба в метрах,  кг/м3 – плотность воды, а
кг/м3 – плотность воды, а 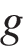 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
Решение.
Задача сводится к решению неравенства  при заданных значениях плотности воды и ускорении свободного падения:
при заданных значениях плотности воды и ускорении свободного падения:
 м.
м.
Ответ: 2.
Ответ: 2
7. B 12. Некоторая компания продает свою продукцию по цене 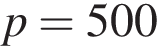 руб. за единицу, переменные затраты на производство одной единицы продукции составляют
руб. за единицу, переменные затраты на производство одной единицы продукции составляют 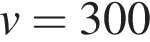 руб., постоянные расходы предприятия
руб., постоянные расходы предприятия  руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле
руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле  . Определите наименьший месячный объeм производства
. Определите наименьший месячный объeм производства 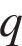 (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.
(единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.
Решение.
Задача сводится к нахождению наименьшего решения неравенства 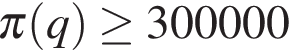 руб. при заданных значениях цены за единицу
руб. при заданных значениях цены за единицу 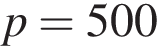 руб., переменных затрат на производство одной единицы продукции
руб., переменных затрат на производство одной единицы продукции 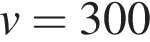 руб. и постоянных расходов предприятия
руб. и постоянных расходов предприятия 
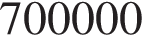 руб. в месяц:
руб. в месяц:
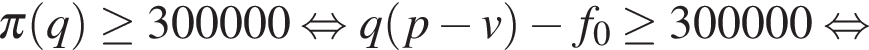

Ответ: 5000.
Ответ: 5000
8. B 12. Расстояние (в км) от наблюдателя, находящегося на небольшой высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле 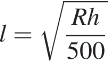 , где
, где  км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах.
км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах.
Решение.
Задача сводится к решению уравнения  при заданном значении R:
при заданном значении R:
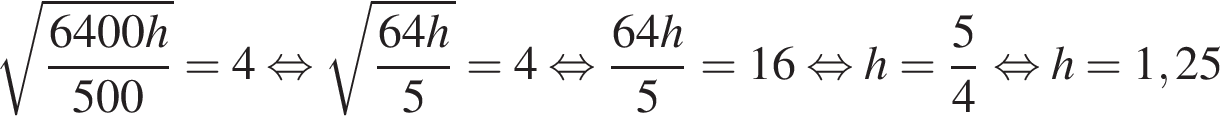 м.
м.
Ответ: 1,25.
Ответ: 1,25
9. B 12. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле  , где
, где  – частота вынуждающей силы (в
– частота вынуждающей силы (в  ),
),  – постоянный параметр,
– постоянный параметр,  – резонансная частота. Найдите максимальную частоту
– резонансная частота. Найдите максимальную частоту  , меньшую резонансной, для которой амплитуда колебаний превосходит величину
, меньшую резонансной, для которой амплитуда колебаний превосходит величину  не более чем на
не более чем на  . Ответ выразите в
. Ответ выразите в  .
.
Решение.
Задача сводится к решению неравенства 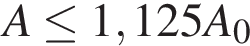 при известном значении резонансной частоты
при известном значении резонансной частоты 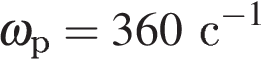 и условии, что частота
и условии, что частота  меньше резонансной:
меньше резонансной:
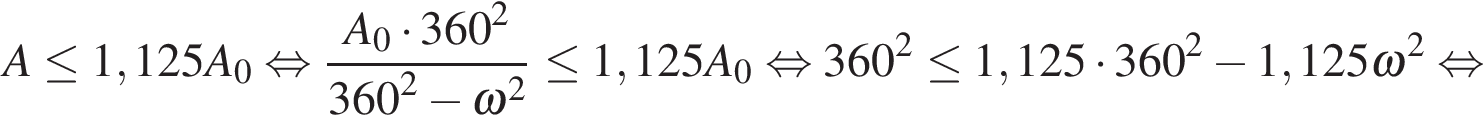
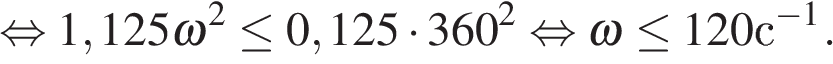
Ответ: 120.
Ответ: 120
10. B 12. Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой
к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой  , где
, где  м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а 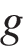 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  м/с
м/с  ). При каком наименьшем значении угла
). При каком наименьшем значении угла  (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
(в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
Вариант № 3711925
1. B 12. В ходе распада радиоактивного изотопа, его масса уменьшается по закону 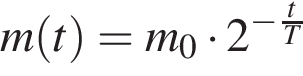 , где
, где  — начальная масса изотопа,
— начальная масса изотопа, 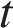 (мин) — прошедшее от начального момента время,
(мин) — прошедшее от начального момента время, 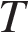 — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени
— период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени  мг изотопа
мг изотопа  , период полураспада которого
, период полураспада которого  мин. В течение скольких минут масса изотопа будет не меньше 47 мг?
мин. В течение скольких минут масса изотопа будет не меньше 47 мг?
Решение.
Задача сводится к решению неравенства 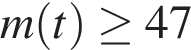 при заданных значениях параметров
при заданных значениях параметров  мг и
мг и  мин:
мин:
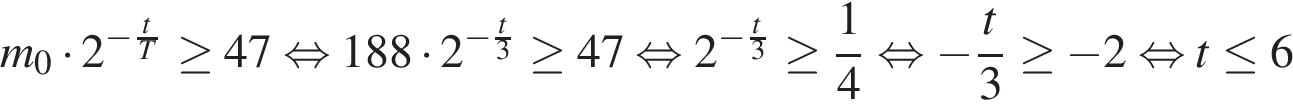 мин.
мин.
Таким образом, масса радиоактивного изотопа будет не меньше 47 мг в течение 6 минут.
Ответ: 6.
Ответ: 6
2. B 12. Водолазный колокол, содержащий в начальный момент времени  моля воздуха объeмом
моля воздуха объeмом  л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма  . Работа, совершаемая водой при сжатии воздуха, определяется выражением
. Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где
(Дж), где  постоянная, а
постоянная, а 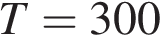 К — температура воздуха. Какой объeм
К — температура воздуха. Какой объeм  (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?
(в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 27 840 Дж?
Решение.
Задача сводится к решению уравнения  при заданных значениях постоянной
при заданных значениях постоянной  , температуры воздуха
, температуры воздуха 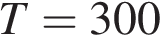 К, количества воздуха
К, количества воздуха  моль и объема воздуха
моль и объема воздуха  л:
л:
 л.
л.
Значит, объем, который будет занимать воздух, равен 3,5 л.
Ответ: 3,5.
Ответ: 3,5
3. B 12. Для обогрева помещения, температура в котором равна  , через радиатор отопления, пропускают горячую воду температурой
, через радиатор отопления, пропускают горячую воду температурой  . Расход проходящей через трубу воды
. Расход проходящей через трубу воды  кг/с. Проходя по трубе расстояние
кг/с. Проходя по трубе расстояние 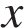 (м), вода охлаждается до температуры
(м), вода охлаждается до температуры  , причeм
, причeм  (м), где
(м), где  — теплоeмкость воды,
— теплоeмкость воды,  — коэффициент теплообмена, а
— коэффициент теплообмена, а  — постоянная. До какой температуры (градусах Цельсия) охладится вода, если длина трубы 144 м?
— постоянная. До какой температуры (градусах Цельсия) охладится вода, если длина трубы 144 м?
Решение.
Задача сводится к решению уравнения  при заданных значениях теплоёмкости воды
при заданных значениях теплоёмкости воды  , коэффициента теплообмена
, коэффициента теплообмена  , постоянной
, постоянной  , температуры помещения
, температуры помещения  и расхода воды
и расхода воды  :
:

 .
.
Ответ: 34.
Ответ: 34
4. B 12. Водолазный колокол, содержащий в начальный момент времени  моля воздуха объeмом
моля воздуха объeмом 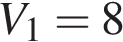 л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма  . Работа, совершаемая водой при сжатии воздуха, определяется выражением
. Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где
(Дж), где  – постоянная, а
– постоянная, а 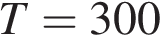 – температура воздуха. Какой объeм
– температура воздуха. Какой объeм  (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10350 Дж?
(в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10350 Дж?
Решение.
Задача сводится к решению уравнения 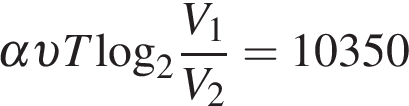 при заданных значениях постоянной
при заданных значениях постоянной  , температуры воздуха
, температуры воздуха 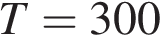 К, количества воздуха
К, количества воздуха  моль и объема воздуха
моль и объема воздуха 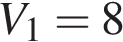 л:
л:
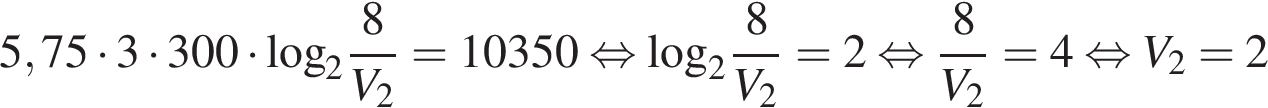 л.
л.
Ответ: 2.
Ответ: 2
5. B 12. Небольшой мячик бросают под острым углом  к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой
к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой  , где
, где  м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а 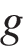 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  м/с
м/с  ). При каком наименьшем значении угла
). При каком наименьшем значении угла  (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
(в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
Решение.
Задача сводится к решению неравенства  на интервале
на интервале  при заданных значениях начальной скорости
при заданных значениях начальной скорости  и ускорения свободного падения
и ускорения свободного падения  :
:

 .
.
Ответ: 30.
Ответ: 30
6. B 12. При адиабатическом процессе для идеального газа выполняется закон  где
где 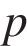 — давление в газе в паскалях,
— давление в газе в паскалях, 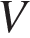 — объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него
— объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него  ) из начального состояния, в котором
) из начального состояния, в котором  Па
Па  , газ начинают сжимать. Какой наибольший объeм
, газ начинают сжимать. Какой наибольший объeм 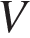 может занимать газ при давлениях
может занимать газ при давлениях 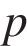 не ниже
не ниже  Па? Ответ выразите в кубических метрах.
Па? Ответ выразите в кубических метрах.
Решение.
Поскольку произведение давления на степень объёма постоянно, а давление не ниже  , при заданных значениях параметров
, при заданных значениях параметров  и
и  Па
Па  м5 имеем неравенство:
м5 имеем неравенство:
 .
.
Значит, наибольший объем, который может занимать газ, равен 8 м3.
Ответ: 8.
Ответ: 8
7. B 12. Уравнение процесса, в котором участвовал газ, записывается в виде  , где
, где 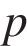 (Па) – давление в газе,
(Па) – давление в газе, 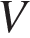 – объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
– объeм газа в кубических метрах, a – положительная константа. При каком наименьшем значении константы a уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
Решение.
Пусть 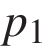 и
и  – начальные, а
– начальные, а  и
и  – конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства
– конечные значения объема и давления газа, соответственно. Задача сводится к решению неравенства  , причем
, причем  :
:
 .
.
Ответ: 2.
Ответ: 2
8. B 12. Плоский замкнутый контур площадью 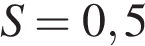 м
м  находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой
находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой  , где
, где  – острый угол между направлением магнитного поля и перпендикуляром к контуру,
– острый угол между направлением магнитного поля и перпендикуляром к контуру,  Тл/с – постоянная,
Тл/с – постоянная, 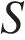 – площадь замкнутого контура, находящегося в магнитном поле (в м
– площадь замкнутого контура, находящегося в магнитном поле (в м  ). При каком минимальном угле
). При каком минимальном угле  (в градусах) ЭДС индукции не будет превышать
(в градусах) ЭДС индукции не будет превышать  В?
В?
Решение.
Задача сводится к решению неравенства 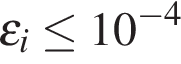 на интервале
на интервале  при заданных значениях площади контура
при заданных значениях площади контура  и постоянной
и постоянной 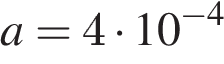 Тл/с:
Тл/с:
 .
.
Ответ: 60.
Ответ: 60
9. B 12. Катер должен пересечь реку шириной  м и со скоростью течения
м и со скоростью течения  м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением
м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением  , где
, где  – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом
– острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом  (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
(в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
Решение.
Задача сводится к решению неравенства 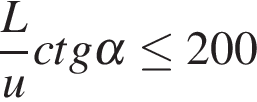 на интервале
на интервале  при заданных значениях длины реки
при заданных значениях длины реки  м и скорости течения
м и скорости течения  м/с:
м/с:
 .
.
Ответ: 45.
Ответ: 45
10. B 12. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле  , где
, где  м/с – скорость звука в воде,
м/с – скорость звука в воде,  – частота испускаемых импульсов (в МГц),
– частота испускаемых импульсов (в МГц),  – частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала
– частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала  , если скорость погружения батискафа не должна превышать 2 м/с.
, если скорость погружения батискафа не должна превышать 2 м/с.
Вариант № 3712153
1. B 12. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна  , где
, где  – масса воды в килограммах,
– масса воды в килограммах,  скорость движения ведeрка в м/с,
скорость движения ведeрка в м/с,  – длина верeвки в метрах, g – ускорение свободного падения (считайте
– длина верeвки в метрах, g – ускорение свободного падения (считайте  м/с
м/с  ). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.
). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.
Решение.
Задача сводится к решению неравенства  при заданной длине верёвки
при заданной длине верёвки  м:
м:


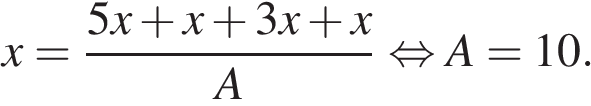
 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением
км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 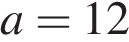 км/ч
км/ч  . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением
. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 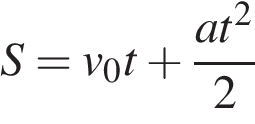 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.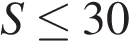 км. Задача сводится к нахождению наибольшего решения неравенства
км. Задача сводится к нахождению наибольшего решения неравенства  и
и 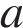 :
:
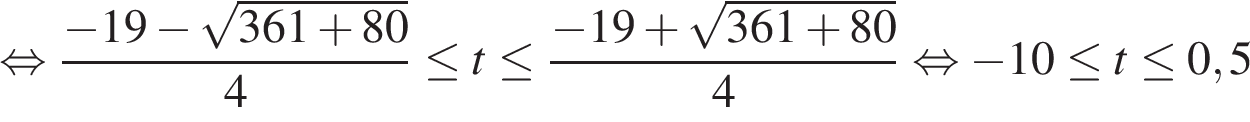
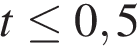 ч, то есть
ч, то есть 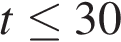 мин.
мин. , где
, где  – длина ребра куба в метрах,
– длина ребра куба в метрах,  кг/м3 – плотность воды, а
кг/м3 – плотность воды, а 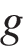 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте  Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах. при заданных значениях плотности воды и ускорении свободного падения:
при заданных значениях плотности воды и ускорении свободного падения: м.
м.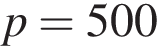 руб. за единицу, переменные затраты на производство одной единицы продукции составляют
руб. за единицу, переменные затраты на производство одной единицы продукции составляют 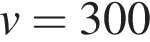 руб., постоянные расходы предприятия
руб., постоянные расходы предприятия  руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле
руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле  . Определите наименьший месячный объeм производства
. Определите наименьший месячный объeм производства 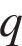 (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.
(единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.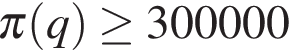 руб. при заданных значениях цены за единицу
руб. при заданных значениях цены за единицу 
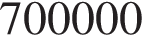 руб. в месяц:
руб. в месяц: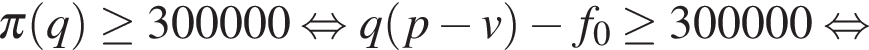

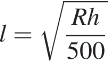 , где
, где  км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах.
км — радиус Земли. На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не менее 4 километров? Ответ выразите в метрах. при заданном значении R:
при заданном значении R: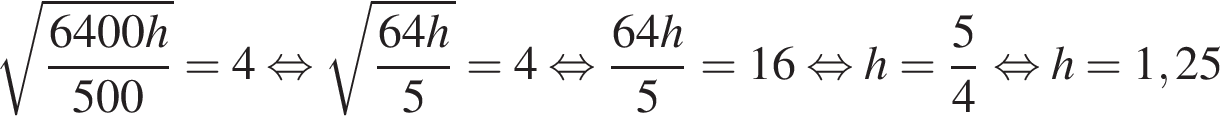 м.
м. , где
, где  – частота вынуждающей силы (в
– частота вынуждающей силы (в  ),
),  – постоянный параметр,
– постоянный параметр,  – резонансная частота. Найдите максимальную частоту
– резонансная частота. Найдите максимальную частоту  . Ответ выразите в
. Ответ выразите в 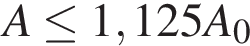 при известном значении резонансной частоты
при известном значении резонансной частоты 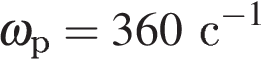 и условии, что частота
и условии, что частота 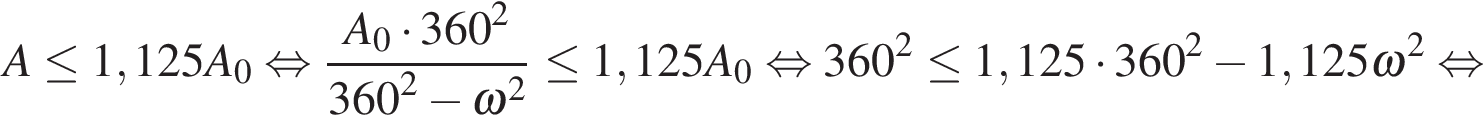
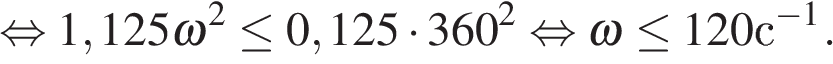
 к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой
к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой  , где
, где  м/с – начальная скорость мячика, а
м/с – начальная скорость мячика, а  м/с
м/с 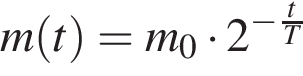 , где
, где  — начальная масса изотопа,
— начальная масса изотопа, 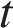 (мин) — прошедшее от начального момента время,
(мин) — прошедшее от начального момента время, 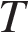 — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени
— период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени  мг изотопа
мг изотопа  , период полураспада которого
, период полураспада которого  мин. В течение скольких минут масса изотопа будет не меньше 47 мг?
мин. В течение скольких минут масса изотопа будет не меньше 47 мг?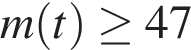 при заданных значениях параметров
при заданных значениях параметров 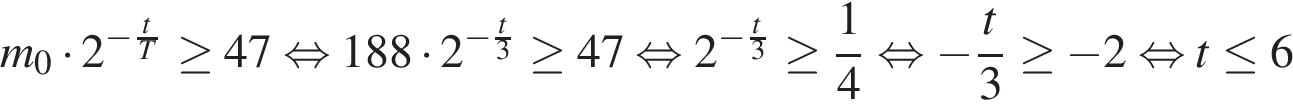 мин.
мин. моля воздуха объeмом
моля воздуха объeмом  л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма  . Работа, совершаемая водой при сжатии воздуха, определяется выражением
. Работа, совершаемая водой при сжатии воздуха, определяется выражением  (Дж), где
(Дж), где  постоянная, а
постоянная, а 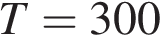 К — температура воздуха. Какой объeм
К — температура воздуха. Какой объeм  при заданных значениях постоянной
при заданных значениях постоянной  , температуры воздуха
, температуры воздуха  л.
л. , через радиатор отопления, пропускают горячую воду температурой
, через радиатор отопления, пропускают горячую воду температурой  . Расход проходящей через трубу воды
. Расход проходящей через трубу воды  кг/с. Проходя по трубе расстояние
кг/с. Проходя по трубе расстояние 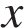 (м), вода охлаждается до температуры
(м), вода охлаждается до температуры  , причeм
, причeм  (м), где
(м), где  — теплоeмкость воды,
— теплоeмкость воды,  — коэффициент теплообмена, а
— коэффициент теплообмена, а  — постоянная. До какой температуры (градусах Цельсия) охладится вода, если длина трубы 144 м?
— постоянная. До какой температуры (градусах Цельсия) охладится вода, если длина трубы 144 м? при заданных значениях теплоёмкости воды
при заданных значениях теплоёмкости воды  , коэффициента теплообмена
, коэффициента теплообмена  , постоянной
, постоянной  , температуры помещения
, температуры помещения  и расхода воды
и расхода воды  :
:
 .
. моля воздуха объeмом
моля воздуха объeмом 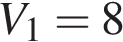 л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма  – постоянная, а
– постоянная, а 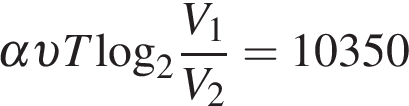 при заданных значениях постоянной
при заданных значениях постоянной  , температуры воздуха
, температуры воздуха 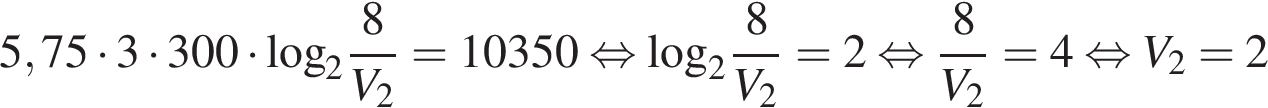 л.
л. на интервале
на интервале  при заданных значениях начальной скорости
при заданных значениях начальной скорости  и ускорения свободного падения
и ускорения свободного падения  :
:
 .
. где
где 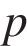 — давление в газе в паскалях,
— давление в газе в паскалях, 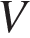 — объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него
— объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него  ) из начального состояния, в котором
) из начального состояния, в котором  Па
Па  , газ начинают сжимать. Какой наибольший объeм
, газ начинают сжимать. Какой наибольший объeм  Па? Ответ выразите в кубических метрах.
Па? Ответ выразите в кубических метрах. м5 имеем неравенство:
м5 имеем неравенство: .
. , где
, где 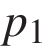 и
и  – начальные, а
– начальные, а  и
и  , причем
, причем  :
: .
.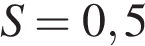 м
м  , где
, где  Тл/с – постоянная,
Тл/с – постоянная, 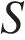 – площадь замкнутого контура, находящегося в магнитном поле (в м
– площадь замкнутого контура, находящегося в магнитном поле (в м  В?
В?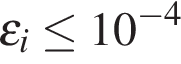 на интервале
на интервале  и постоянной
и постоянной 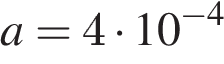 Тл/с:
Тл/с: .
. м и со скоростью течения
м и со скоростью течения  м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением
м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением  , где
, где 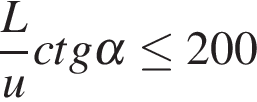 на интервале
на интервале  .
. , где
, где  м/с – скорость звука в воде,
м/с – скорость звука в воде,  – частота испускаемых импульсов (в МГц),
– частота испускаемых импульсов (в МГц),  – частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала
– частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала  , где
, где  – масса воды в килограммах,
– масса воды в килограммах,  скорость движения ведeрка в м/с,
скорость движения ведeрка в м/с,  – длина верeвки в метрах, g – ускорение свободного падения (считайте
– длина верeвки в метрах, g – ускорение свободного падения (считайте  при заданной длине верёвки
при заданной длине верёвки  м:
м:



