Решение. 7 страница
Ответ: 10. Ответ: 10 8. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: -12. Ответ: -12 9. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 16. Ответ: 16 10. B 11. Найдите значение выражения
Вариант № 3711413 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 18. Ответ: 18 2. B 11. Найдите Решение. Поскольку
Ответ: -17. Ответ: -17 3. B 11. Найдите значение выражения Решение. Сходственные функции дополнительных углов равны, поэтому
Ответ: 5. Ответ: 5 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 16. Ответ: 16 5. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 2. Ответ: 2 6. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 7. Ответ: 7 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 14. Ответ: 14 8. B 11. Найдите Решение. Покажем, что числитель дроби равен знаменателю:
Таким образом,
Ответ: 1. Ответ: 1 9. B 11. Найдите Решение. Подставим аргументы в формулу, задающую функцию:
Следовательно, Ответ: 0. Ответ: 0 10. B 11. Найдите значение выражения
Вариант № 3711431 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: -12. Ответ: -12 2. B 11. Найдите Решение. Способ 1:
Способ 2: Поделим числитель и знаменатель дроби на
Ответ: 5. Ответ: 5 3. B 11. Найдите Решение. Выполним преобразования:
Ответ: 71. Ответ: 71 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 6. Ответ: 6 5. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 31. Ответ: 31 6.B 11. Найдите значение выражения Решение. Выполним действия в скобках:
Тогда
Ответ: -367. Ответ: -367 7. B 11. Найдите Решение. Выполним преобразования:
Поскольку угол
Ответ: 0,6. Ответ: 0,6 8. B 11. Найдите Решение. Поскольку угол
Ответ: −10. Ответ: -10 9. B 11. Найдите значение выражения Решение. Умножим числитель и знаменатель на 10 000:
Ответ: 10. Ответ: 10 10. B 11. Найдите значение выражения
Вариант № 3711455 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 32. Ответ: 32 2. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 28. Ответ: 28 3. B 11. Найдите Решение. Подставляя аргументы в формулу, задающую функцию, получаем:
Ответ: 14. Ответ: 14 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 2. Ответ: 2 5. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: -5. Ответ: -5 6. B 11. Найдите значение выражения Решение. Используем формулу косинуса двойного угла
Ответ: −1,5. Ответ: -1,5 7. B 11. Найдите Решение. Поскольку угол
Ответ: 1. Ответ: 1 8. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: -12. Ответ: -12 9. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 3. Ответ: 3 B 11. Найдите значение выражения
Вариант № 3711494 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 42. Ответ: 42 2. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 7. Ответ: 7 3. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 7. Ответ: 7 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 0. Ответ: 0 5. B 11. Найдите значение выражения Решение. Выполним преобразования:
При Ответ: 2. Ответ: 2 6. B 11. Найдите Решение. Используем свойство пропорции:
Следовательно,
Ответ: 2,25. Ответ: 2,25 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 22. Ответ: 22 8. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 1,4. Ответ: 1,4 9. B 11. Найдите значение выражения Решение. Используем формулу синуса двойного угла
Ответ: 2. Ответ: 2 10. B 11. Найдите значение выражения
Вариант № 3711725 1. B 12. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону Решение. Задача сводится к решению уравнения
На протяжении первой секунды лампочка будет гореть Ответ: 50. Ответ: 50 2. B 12. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой Решение. Задача сводится к нахождению наибольшего решения неравенства
Решая квадратное неравенство методом интервалов, получим Ответ: 5. Ответ: 5 3. B 12. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна Решение. Задача сводится к решению неравенства
Ответ: 2. Ответ: 2 4. B 12. Расстояние (в км) от наблюдателя, находящегося на небольшой высоте Решение. Задача сводится к решению уравнений
Примечание. Заметим, что полученная величина равна 1,25 метра, т. е. соответствует уровню глаз ребенка. Ответ: 0,00125. Ответ: 0,00125 5. B 12. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле Решение. Задача сводится к решению неравенства
Ответ: 751. Ответ: 751 6. B 12. Автомобиль, движущийся в начальный момент времени со скоростью
|

 .
. .
. .
. .
. .
. при
при  .
. .
. , если
, если  .
. . Тогда
. Тогда .
.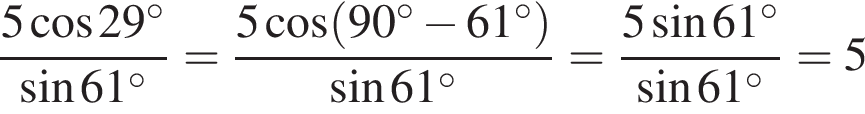 .
.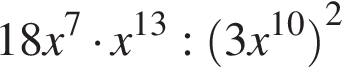 .
.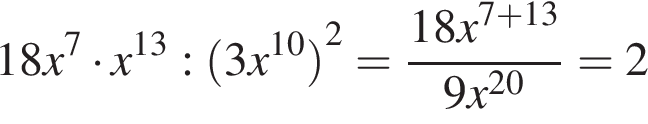 .
. .
. .
.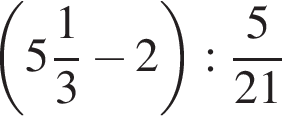 .
.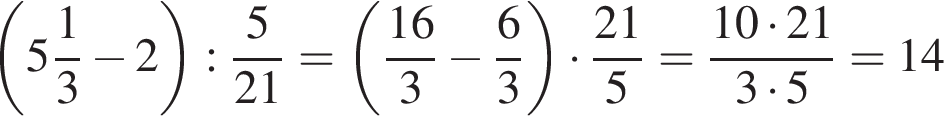 .
. , если
, если  , при
, при  .
.

 .
. , если
, если 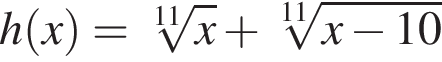 .
.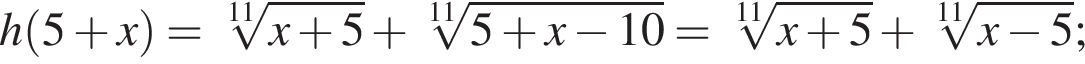
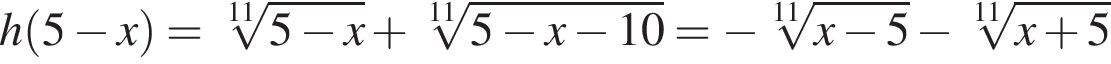 .
. .
. .
. , если
, если  .
. .
. , если
, если  .
. . Тогда:
. Тогда: .
. :
: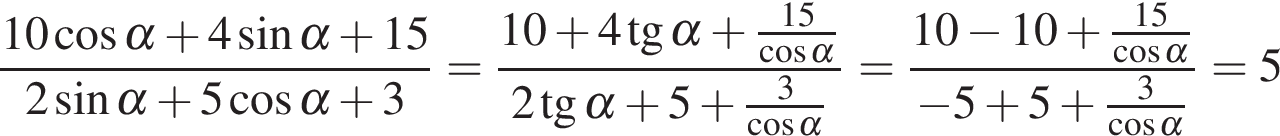 .
. , если
, если  .
. .
. , если
, если  , а
, а  .
.
 , если
, если  .
. .
. при
при  .
. .
. .
. , если
, если  и
и  .
. .
. лежит в второй четверти,
лежит в второй четверти, 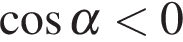 . Тогда
. Тогда .
. , если
, если  и
и 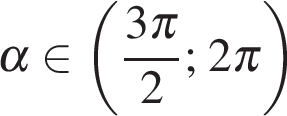 .
.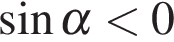 . Применим формулу приведения, а затем выразим синус через косинус. Имеем:
. Применим формулу приведения, а затем выразим синус через косинус. Имеем: .
. .
. .
. .
. при
при  .
. .
. .
. .
. , если
, если  .
. .
. .
. .
. .
. .
.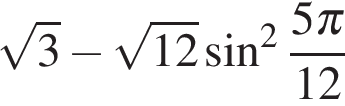 .
. :
: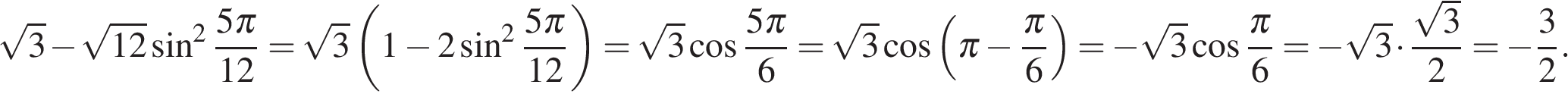
 , если
, если  и
и 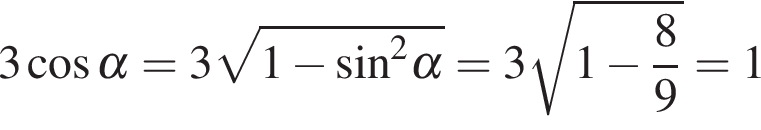 .
.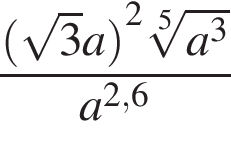 при
при 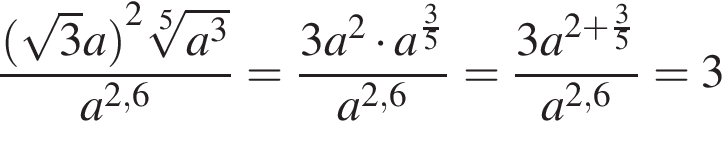 .
. .
. .
.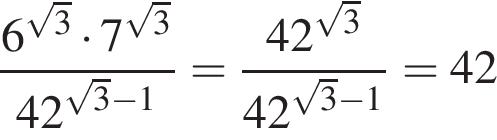 .
. .
. .
. при
при  .
.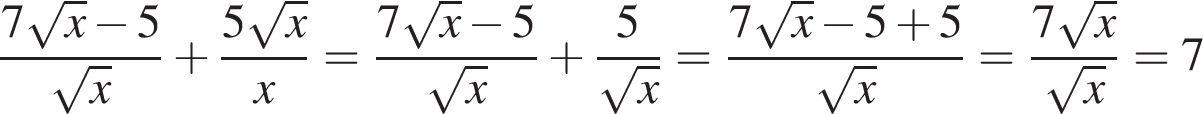 .
. , если
, если  .
. .
.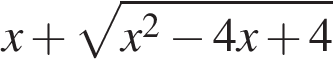 при
при  .
.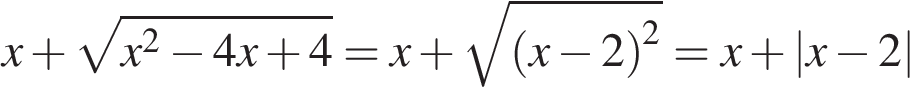 .
. . Тогда
. Тогда  .
. , если
, если  .
.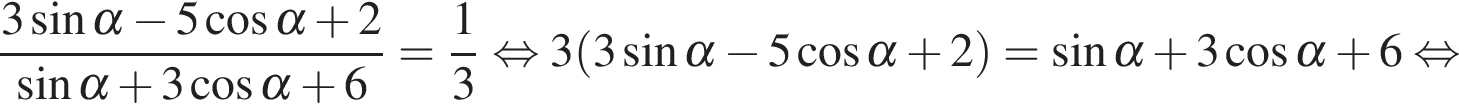
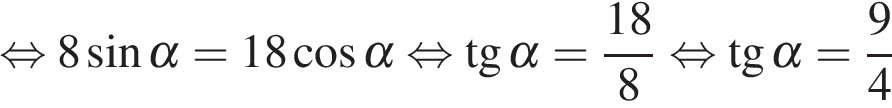 .
.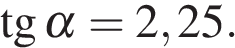
 , если
, если  .
. .
. .
. .
. .
. :
:
 , если
, если  .
. , где
, где 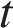 – время в секундах, амплитуда
– время в секундах, амплитуда  В, частота
В, частота  /с, фаза
/с, фаза  . Датчик настроен так, что если напряжение в нeм не ниже чем
. Датчик настроен так, что если напряжение в нeм не ниже чем  В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть? при заданных значениях амплитуды сигнала, частоты и фазы:
при заданных значениях амплитуды сигнала, частоты и фазы:

 с, то есть
с, то есть  % времени.
% времени. кг и радиуса
кг и радиуса  см, и двух боковых с массами
см, и двух боковых с массами  кг и с радиусами
кг и с радиусами  . При этом момент инерции катушки относительно оси вращения, выражаемый в
. При этом момент инерции катушки относительно оси вращения, выражаемый в  , даeтся формулой
, даeтся формулой  При каком максимальном значении
При каком максимальном значении  момент инерции катушки не превышает предельного значения 625
момент инерции катушки не превышает предельного значения 625  км при заданных значениях параметров
км при заданных значениях параметров  ,
,  и
и  :
:
 . Наибольшее решение двойного неравенства — число 5.
. Наибольшее решение двойного неравенства — число 5. , где
, где  скорость движения ведeрка в м/с,
скорость движения ведeрка в м/с,  – длина верeвки в метрах, g – ускорение свободного падения (считайте
– длина верeвки в метрах, g – ускорение свободного падения (считайте  м/с
м/с  ). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.
). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с. при заданной длине верёвки
при заданной длине верёвки  м:
м:
 , где
, где  (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
(км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах. при заданном значении R:
при заданном значении R:
 , где
, где  м/с – скорость звука в воде,
м/с – скорость звука в воде,  – частота испускаемых импульсов (в МГц),
– частота испускаемых импульсов (в МГц),  – частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала
– частота отражeнного от дна сигнала, регистрируемая приeмником (в МГц). Определите наибольшую возможную частоту отраженного сигнала  м/с при известных значениях
м/с при известных значениях  МГц – частоты испускаемых импульсов:
МГц – частоты испускаемых импульсов: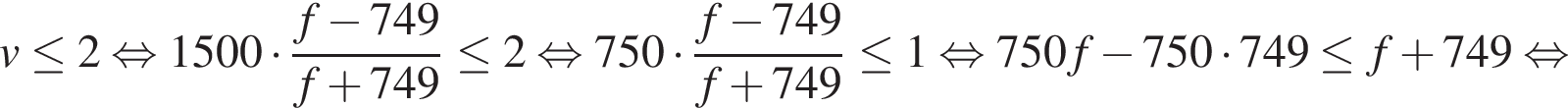
 МГц.
МГц. м/с, начал торможение с постоянным ускорением
м/с, начал торможение с постоянным ускорением  м/с2. За
м/с2. За  (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.


