Решение. 5 страница
2. B 10. Решение. В правильной пирамиде вершина проецируется в центр основания, следовательно
Ответ: 17. Ответ: 17 3. B 10. Решение. Объем данного многогранника равен разнице объемов параллелепипедов со сторонами 5, 5, 4 и 1, 2, 5:
Ответ: 90. Ответ: 90 4. B 10. Решение. Объем конуса равен
где Ответ: 2,25. Ответ: 2,25 5. B 10. Решение. По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 9/12 исходного объема:
Ответ: 1500. Ответ: 1500 6. B 10. Решение. Третья сторона треугольника в основании равна 10 и его площадь
Полная площадь поверхности:
Ответ: 288. Ответ: 288 7. B 10. Решение. Найдем площадь грани SBC:
Отрезок SK является медианой равнобедренного треугольника SBC, а значит, и его высотой. Тогда
Ответ: 9. Ответ: 9 8. B 10. Площадь боковой поверхности цилиндра равна Решение.
Ответ: 2 9. B 10.
Решение. Радиус большого круга является радиусом шара. Площадь первого выражается через радиус
Ответ: 12. Ответ: 12 10. B 10. Вариант № 3711050 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 6. Ответ: 6 2. B 11. Найдите значение выражения Решение. Умножим числитель и знаменатель на 10 000:
Ответ: 10. Ответ: 10 3. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 6. Ответ: 6 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 36. Ответ: 36 5. B 11. Найдите Решение. Выполним преобразования:
Ответ: 71. Ответ: 71 6. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 31. Ответ: 31 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 1,4. Ответ: 1,4 8. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 15. Ответ: 15 9. B 11. Найдите Решение. Выполним преобразования:
Ответ: 0. Ответ: 0 10. B 11. Найдите значение выражения
Вариант № 3711101 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 16. Ответ: 16 2. B 11. Найдите Решение. Разделим числитель и знаменатель на
Тогда
Ответ: 8. Ответ: 8 3. B 11. Найдите Решение. Покажем, что числитель дроби равен знаменателю:
Таким образом,
Ответ: 1. Ответ: 1 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: -2. Ответ: -2 5. B 11. Найдите значение выражения Решение. В силу периодичности косинуса и симметричности синуса
Ответ: 0,4. Ответ: 0,4 6. B 11. Найдите Решение. Поскольку
Ответ: -17. Ответ: -17 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 7. Ответ: 7 8.B 11. Найдите значение выражения Решение. В силу нечетности и периодичности синуса
Ответ: 4. Ответ: 4 9. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 1,4. Ответ: 1,4 10. B 11. Найдите значение выражения
Вариант № 3711111 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 2. Ответ: 2 2. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 0. Ответ: 0 3. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 31. Ответ: 31 4. B 11. Найдите значение выражения Решение.
Ответ: 27. Ответ: 27 5.B 11. Найдите значение выражения Решение. Используем формулу разности квадратов:
Ответ: 333. Ответ: 333 6. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 2. Ответ: 2 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 4. Ответ: 4 8. B 11. Найдите Решение. Пользуемся периодичностью тангенса и используем формулу приведения:
Ответ: −2,5. Ответ: -2,5 9. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 5. Ответ: 5 10. B 11. Найдите значение выражения
Вариант № 3711151 1. B 11. Найдите Решение. Покажем, что числитель дроби равен знаменателю:
Таким образом,
Ответ: 1. Ответ: 1 2. B 11. Найдите Решение. Поскольку угол альфа лежит в четвёртой четверти, его тангенс отрицателен. Поэтому
Ответ: -3. Ответ: -3 3. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 8. Ответ: 8 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 121. Ответ: 121 5. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 18. Ответ: 18 6. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 0,25. Ответ: 0,25 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 3. Ответ: 3 8. B 11. Найдите Решение. Выполним преобразования:
Ответ: -14. Ответ: -14 9. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 1. Ответ: 1 10. B 11. Найдите значение выражения
Вариант № 3711173 1. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 7. Ответ: 7 2. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 1. Ответ: 1 3. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: -5. Ответ: -5 4. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 4. Ответ: 4 5. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 18. Ответ: 18 6. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 0,25. Ответ: 0,25 7. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 2. Ответ: 2 8. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 8. Ответ: 8 9. B 11. Найдите значение выражения Решение. Выполним преобразования:
Ответ: 9. Ответ: 9 10. B 11. Найдите значение выражения
Вариант № 3711196 1. B 11. Найдите Решение. Способ 1:
Способ 2: Поделим числитель и знаменатель дроби на
|

 В правильной четырехугольной пирамиде
В правильной четырехугольной пирамиде  точка
точка  – центр основания,
– центр основания,  – вершина,
– вершина,  ,
,  . Найдите боковое ребро
. Найдите боковое ребро  .
. является высотой пирамиды. тогда по теореме Пифагора
является высотой пирамиды. тогда по теореме Пифагора
 Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые). .
. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза? ,
, – высота конуса, а
– высота конуса, а  – радиус основания. При увеличении радиуса основания в 1,5 раза объем конуса увеличится в 2,25 раза.
– радиус основания. При увеличении радиуса основания в 1,5 раза объем конуса увеличится в 2,25 раза. В цилиндрический сосуд налили 2000
В цилиндрический сосуд налили 2000  воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в  .
. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности. Площадь боковой поверхности призмы с периметром основания
Площадь боковой поверхности призмы с периметром основания  равна
равна .
.
 В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.
В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.

 , а диаметр основания — 1. Найдите высоту цилиндра.
, а диаметр основания — 1. Найдите высоту цилиндра. Площадь боковой поверхности цилиндра находится по формуле:
Площадь боковой поверхности цилиндра находится по формуле:  , значит,
, значит,  .
. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Площадь большого круга шара равна 3. Найдите площадь поверхности шара. , а площадь поверхности сферы – как
, а площадь поверхности сферы – как  . Видно, что площадь поверхности шара в
. Видно, что площадь поверхности шара в  раза больше площади поверхности большого круга.
раза больше площади поверхности большого круга. Объем треугольной пирамиды
Объем треугольной пирамиды  , являющейся частью правильной шестиугольной пирамиды
, являющейся частью правильной шестиугольной пирамиды  , равен 1. Найдите объем шестиугольной пирамиды.
, равен 1. Найдите объем шестиугольной пирамиды.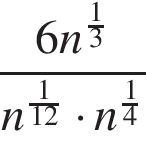 при
при  .
.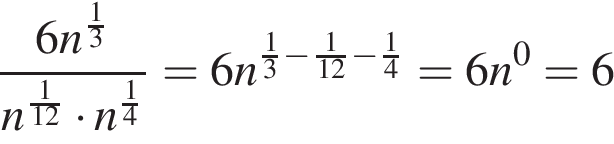 .
. .
. .
. , если
, если  , а
, а  .
.
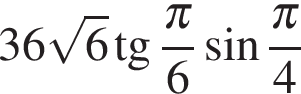 .
.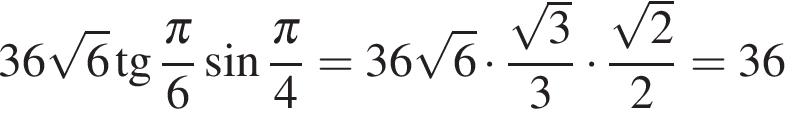 .
. , если
, если  .
. .
. .
. .
. .
. .
. .
. .
. , если
, если 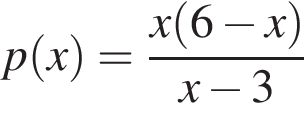 при
при 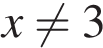 .
.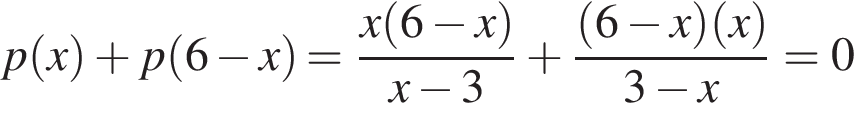 .
. при
при  .
. .
. .
.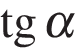 , если
, если  .
. :
: .
. .
.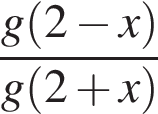 , если
, если  при
при 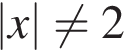 .
.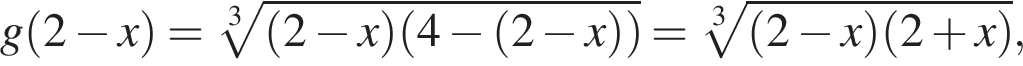
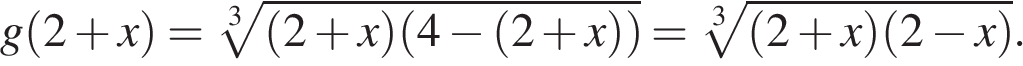
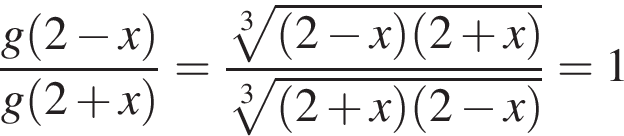 .
. .
.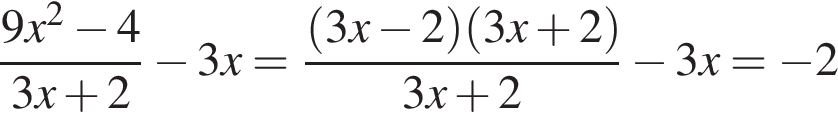 .
.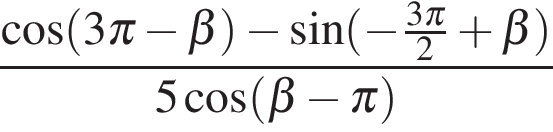 .
.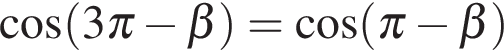 ,
, 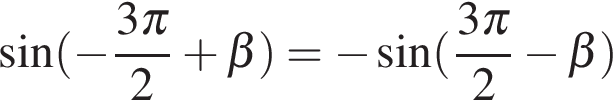 . Далее используем формулы приведения:
. Далее используем формулы приведения: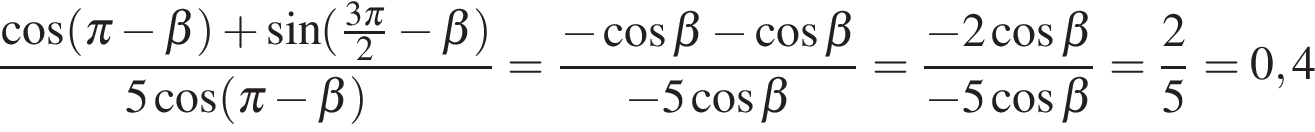 .
. , если
, если  .
. . Тогда
. Тогда .
. .
. .
.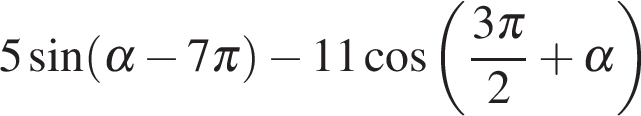 , если
, если  .
. . Далее по формулам приведения имеем:
. Далее по формулам приведения имеем: .
.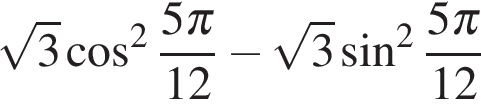 .
. .
. .
. .
. .
.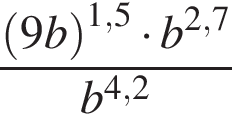 при
при  .
.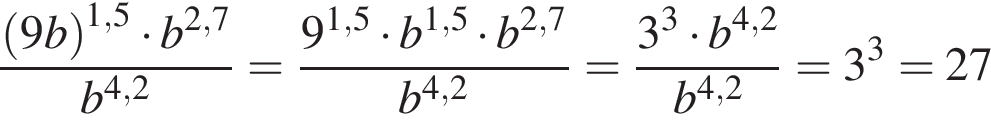 .
. .
. .
. .
. .
. .
. , если
, если 

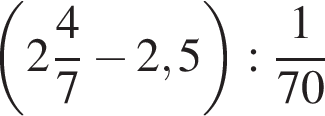 .
. .
.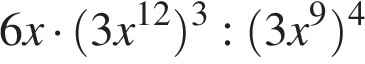 при
при 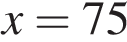 .
. , если
, если  , при
, при  .
.

 .
. и
и 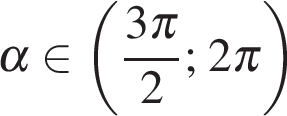 .
. .
. .
. .
. при
при  .
. .
. при
при  .
. .
. при
при  .
. .
. .
. , если
, если  .
. .
.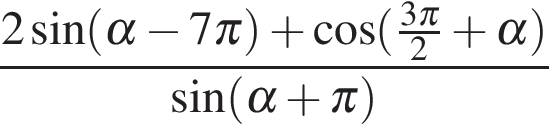 .
. .
. при
при  .
. .
.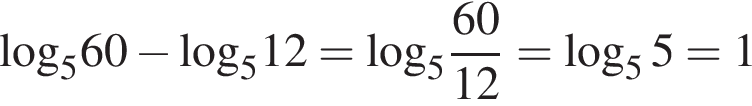 .
. .
. .
. .
.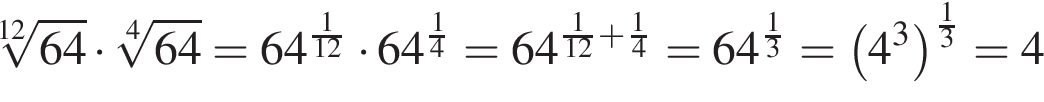 .
. .
. .
. .
. .
. при
при  .
. .
. , если
, если  .
. . Тогда:
. Тогда: .
.


