Вариант № 3713210
1. B 13.  Найдите объем
Найдите объем 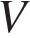 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной части цилиндра равен
 .
.
Ответ: 3,75.
Ответ: 3,75
2. B 13. 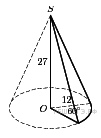 Найдите объем
Найдите объем 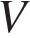 части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной части конуса равен
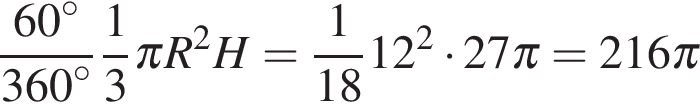 .
.
Ответ: 216.
Ответ: 216
3. B 13.  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение.
Объем прямой призмы равен 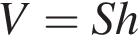 где
где  – площадь основания, а
– площадь основания, а 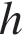 – боковое ребро. Тогда объем равен
– боковое ребро. Тогда объем равен
 .
.
Ответ: 120.
Ответ: 120
4. B 13. 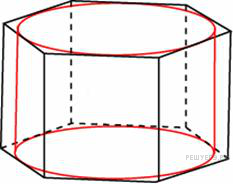 Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.
Решение.
Сторона правильного шестиугольника  выражается через радиус
выражается через радиус  вписанной в него окружности как
вписанной в него окружности как 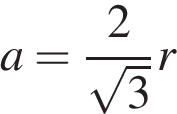 . Тогда площадь боковой поверхности призмы выражается формулой
. Тогда площадь боковой поверхности призмы выражается формулой
 .
.
Ответ: 24.
Ответ: 24
5. B 13.  Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30  . В ответе укажите
. В ответе укажите  .
.
Решение.
Объем конуса равен
 ,
,
где  – площадь основания, а
– площадь основания, а 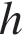 – высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в
– высота конуса. Высоту конуса найдем по свойству стороны прямоугольного треугольника, находящейся напротив угла в  ° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
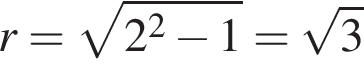 .
.
Тогда объем
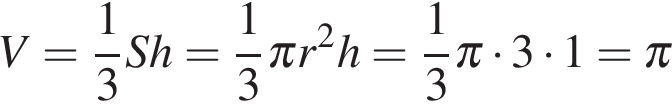 .
.
Ответ: 1.
Ответ: 1
6. B 13. 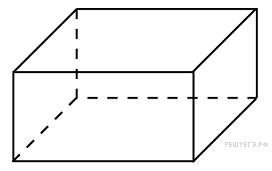 Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Решение.
Объем прямоугольного параллелепипеда равен 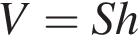 , где
, где  – площадь грани, а
– площадь грани, а 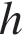 — высота перпендикулярного к ней ребра. Имеем
— высота перпендикулярного к ней ребра. Имеем
 .
.
Ответ: 48.
Ответ: 48
7. B 13.  В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите тангенс угла
все ребра равны 1. Найдите тангенс угла 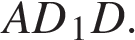
Решение.
Рассмотрим прямоугольный треугольник  катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:
катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:  . Поскольку
. Поскольку  имеем:
имеем:
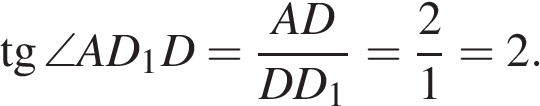
Ответ: 2.
Ответ: 2
8. B 13.  Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на  .
.
Решение.
Радиус основания конуса  равен половине диагонали квадрата
равен половине диагонали квадрата  :
:  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на  :
:
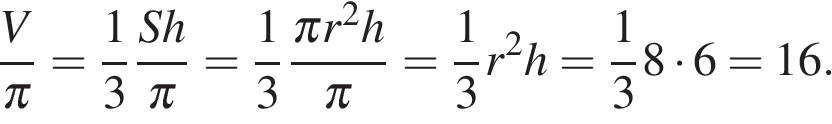
Ответ: 16.
Ответ: 16
9. B 13. 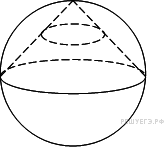
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Решение.
Запишем формулу для объёма шара:
 .
.
Объём конуса в 4 раза меньше:
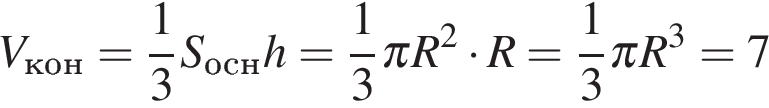 .
.
Ответ: 7.
Ответ: 7
10. B 13.  Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Вариант № 3713330
1. B 13. 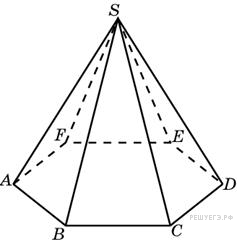 Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Решение.
Площадь основания равна
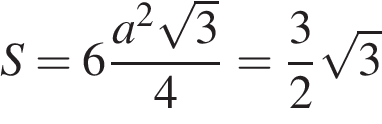 .
.
Из формулы для объема пирамиды найдем высоту:
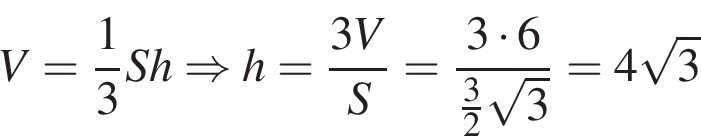 .
.
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:
 .
.
Ответ: 7.
Ответ: 7
2. B 13. 
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Решение.
 ..
..
Ответ: 24.
Ответ: 24
3. B 13. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Решение.
Объем такого шара
 ,
,
откуда получим, что  .
.
Ответ: 12.
Ответ: 12
4. B 13. 
Найдите объем правильной шестиугольной призмы, все ребра которой равны  .
.
Решение.
Объем призмы равен произведению площади основания на высоту. Высотой правильной призмы является ее боковое ребро. Основание призмы — правильный шестиугольник. Площадь правильного шестиугольника со стороной  вычисляется по формуле
вычисляется по формуле  . Следовательно,
. Следовательно,
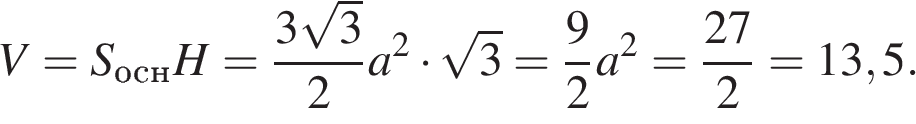
Ответ: 13,5.
Ответ: 13,5
5. B 13.  Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на  .
.
Решение.
В треугольнике, образованном радиусом основания r, высотой h и образующей конуса l, углы при образующей равны, поэтому высота конуса равна радиусу его основания: h = r. Тогда объем конуса, деленный на  вычисляется следующим образом:
вычисляется следующим образом:
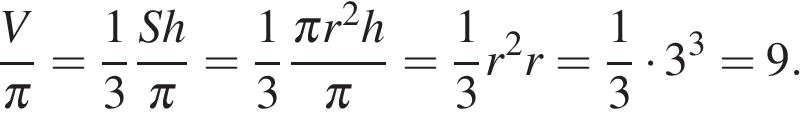
Ответ: 9.
Ответ: 9
6. B 13. 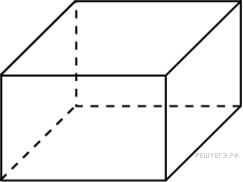 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Решение.
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме попарных произведений его измерений
 .
.
Ответ: 22.
Ответ: 22
7. B 13.  Найдите объем
Найдите объем 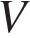 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной части цилиндра равен
 .
.
Ответ: 937,5.
Ответ: 937,5
8. B 13.  Диагональ прямоугольного параллелепипеда равна
Диагональ прямоугольного параллелепипеда равна  и образует углы 30
и образует углы 30  , 30
, 30  и 45
и 45  с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Решение.
Ребро параллелепипеда напротив угла в 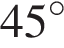 равно
равно  , поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в
, поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в  и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
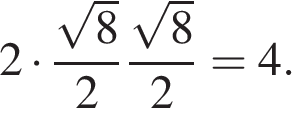
Ответ: 4.
Ответ: 4
9. B 13.  Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60  . Высота пирамиды равна 6. Найдите объем пирамиды.
. Высота пирамиды равна 6. Найдите объем пирамиды.
Решение.
В треугольниках  и
и  сторона
сторона  — общая,
— общая,  и
и  , поэтому эти треугольники равны; треугольник
, поэтому эти треугольники равны; треугольник  — равносторонний,
— равносторонний,  и
и  . Тогда объем пирамиды
. Тогда объем пирамиды
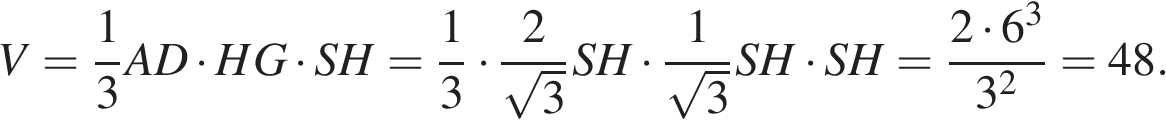
Ответ: 48.
Ответ: 48
10. B 13. 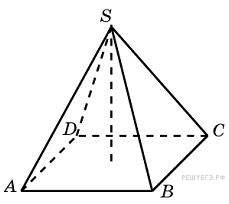 В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Решение.
По теореме Пифагора найдем, что половина диагонали основания равна 8. Тогда диагональ основания равна 16, а сторона – 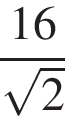 и площадь
и площадь
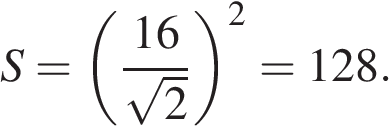
Тогда объем пирамиды
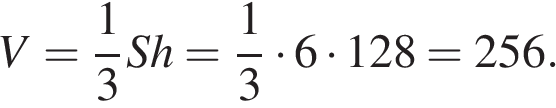
Ответ: 256.
Ответ: 256
Вариант № 3713411
1. B 13.  Диагональ прямоугольного параллелепипеда равна
Диагональ прямоугольного параллелепипеда равна  и образует углы 30
и образует углы 30  , 30
, 30  и 45
и 45  с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Решение.
Ребро параллелепипеда напротив угла в 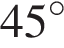 равно
равно  , поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в
, поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в  и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
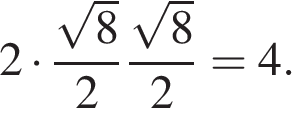
Ответ: 4.
Ответ: 4
2. B 13.  В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы.
Решение.
По теореме Пифагора длина гипотенузы треугольника в основании  . Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
. Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
 .
.
Ответ: 125.
Ответ: 125
3. B 13.  Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2.
, а высота равна 2.
Решение.
Сторона правильного треугольника выражается через радиус описанной окружности как  . Площадь боковой поверхности призмы тогда равна
. Площадь боковой поверхности призмы тогда равна
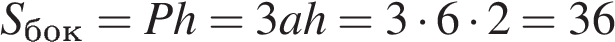 .
.
Ответ: 36.
Ответ: 36
4. B 13.  Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Решение.
Площадь основания равна
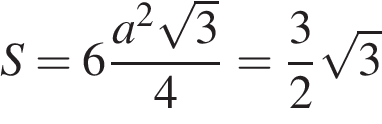 .
.
Из формулы для объема пирамиды найдем высоту:
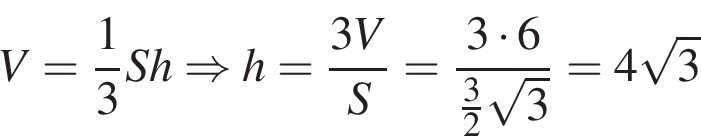 .
.
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:
 .
.
Ответ: 7.
Ответ: 7
5. B 13.  Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Решение.
Площадь боковой поверхности пирамиды равна
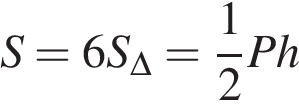 ,
,
где  – периметр основания, а
– периметр основания, а 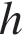 –апофема. Апофему найдем по теореме Пифагора:
–апофема. Апофему найдем по теореме Пифагора:  . Тогда площадь боковой поверхности
. Тогда площадь боковой поверхности
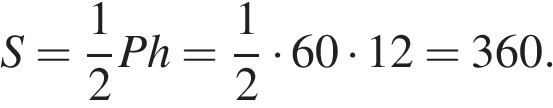
Ответ: 360.
Ответ: 360
6. B 13.  Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  .
.
Решение.
Найдем образующую по теореме Пифагора:  . Площадь полной поверхности конуса
. Площадь полной поверхности конуса
 .
.
Ответ: 24.
Ответ: 24
7. B 13.  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Решение.
Объем прямой призмы равен 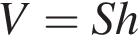 где
где  – площадь основания, а
– площадь основания, а 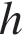 – боковое ребро. Тогда длина ее бокового ребра равна
– боковое ребро. Тогда длина ее бокового ребра равна
 .
.
Ответ: 4.
Ответ: 4
8. B 13.  Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на  .
.
Решение.
Радиус основания конуса  равен половине диагонали квадрата
равен половине диагонали квадрата  :
:  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на  :
:
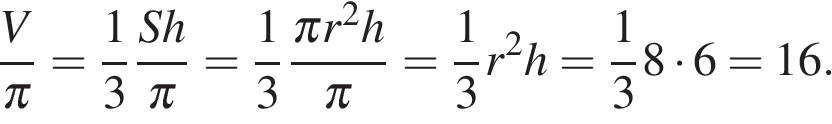
Ответ: 16.
Ответ: 16
9. B 13.  Объем шара равен 288
Объем шара равен 288  . Найдите площадь его поверхности, деленную на
. Найдите площадь его поверхности, деленную на  .
.
Решение.
Объем шара радиуса 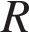 вычисляется по формуле
вычисляется по формуле 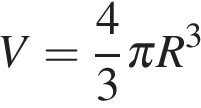 , откуда
, откуда
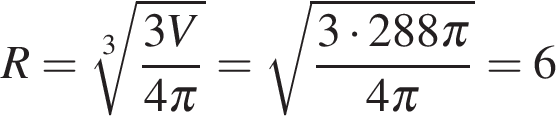 .
.
Площадь его поверхности:
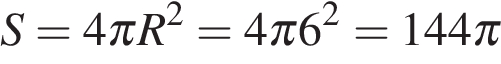 .
.
Ответ: 144.
Ответ: 144
10. B 13.  Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны  .
.
Вариант № 3713471
1. B 13. 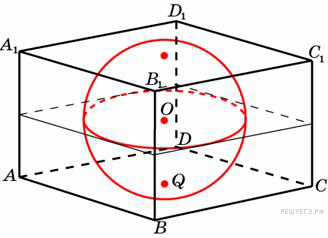 Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Решение.
Высота и сторона такого параллелепипеда равны диаметру сферы, то есть это куб со стороной 2. Площадь поверхности куба со стороной  :
:
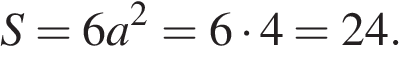
Ответ: 24.
Ответ: 24
2. B 13.  Найдите объем
Найдите объем 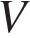 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
.
Решение.
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
 .
.
Ответ: 14.
Ответ: 14
3. B 13.  Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен  .
.
Решение.
Объем пирамиды равен
 ,
,
где  — площадь основания, а
— площадь основания, а 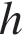 — высота пирамиды. Найдем площадь равностороннего треугольника, лежащего в основании:
— высота пирамиды. Найдем площадь равностороннего треугольника, лежащего в основании:
 .
.
Тогда высота пирамиды равна
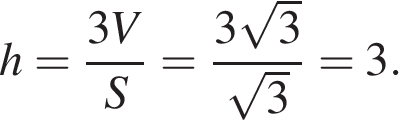
Ответ: 3.
Ответ: 3
4. B 13.  Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Решение.
Объем прямоугольного параллелепипеда равен 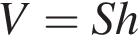 , где
, где  – площадь грани, а
– площадь грани, а 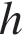 – высота перпендикулярного к ней ребра. Тогда площадь грани
– высота перпендикулярного к ней ребра. Тогда площадь грани
 .
.
Ответ: 8.
Ответ: 8

 Найдите объем
Найдите объем 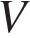 части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите  .
. .
. Найдите объем
Найдите объем 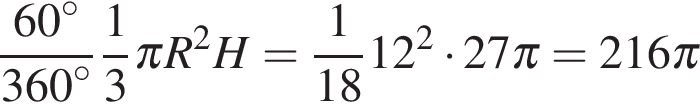 .
. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.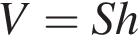 где
где  – площадь основания, а
– площадь основания, а 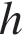 – боковое ребро. Тогда объем равен
– боковое ребро. Тогда объем равен .
. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
, а высота равна 2. выражается через радиус
выражается через радиус  вписанной в него окружности как
вписанной в него окружности как 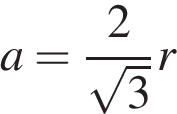 . Тогда площадь боковой поверхности призмы выражается формулой
. Тогда площадь боковой поверхности призмы выражается формулой .
. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30  . В ответе укажите
. В ответе укажите  .
. ,
, ° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора:
° – она вдвое меньше гипотенузы, которой в данном случае является образующая конуса. Радиус основания найдем по теореме Пифагора: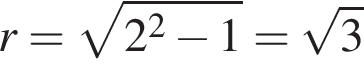 .
.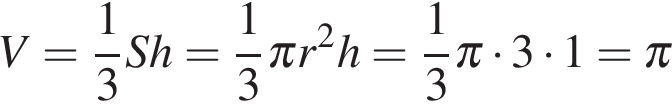 .
. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда. .
. В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите тангенс угла
все ребра равны 1. Найдите тангенс угла 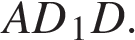
 катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:
катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:  . Поскольку
. Поскольку  имеем:
имеем: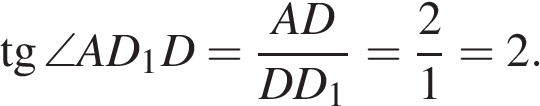
 Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на  .
. :
:  . Тогда объем конуса, деленный на
. Тогда объем конуса, деленный на 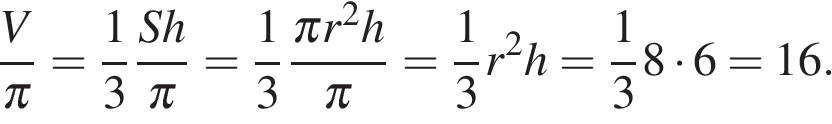

 .
.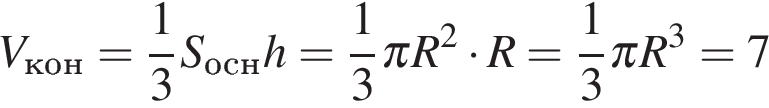 .
. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.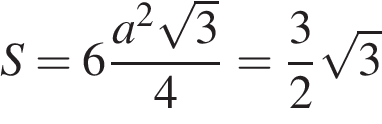 .
.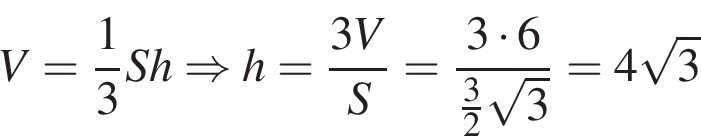 .
. .
. ..
.. ,
, .
.
 . Следовательно,
. Следовательно,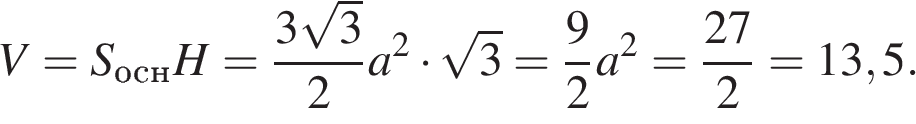
 Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на 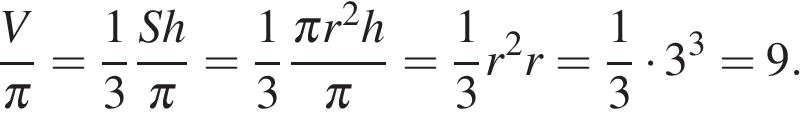
 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности. .
. Найдите объем
Найдите объем  .
. Диагональ прямоугольного параллелепипеда равна
Диагональ прямоугольного параллелепипеда равна  и образует углы 30
и образует углы 30 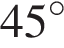 равно
равно  , поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в
, поскольку образует с заданной диагональю и диагональю одной из граней равнобедренный треугольник. Два другие ребра по построению лежат в прямоугольных треугольниках напротив угла в  и равны, поэтому половине диагонали. Тогда объем параллелепипеда:
и равны, поэтому половине диагонали. Тогда объем параллелепипеда: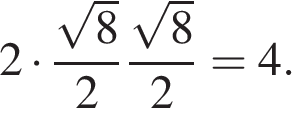
 Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60  и
и  сторона
сторона  — общая,
— общая,  и
и  , поэтому эти треугольники равны; треугольник
, поэтому эти треугольники равны; треугольник  — равносторонний,
— равносторонний,  и
и  . Тогда объем пирамиды
. Тогда объем пирамиды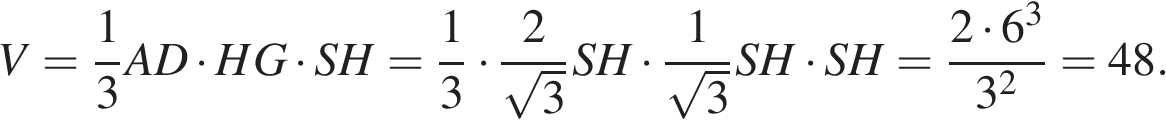
 В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.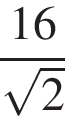 и площадь
и площадь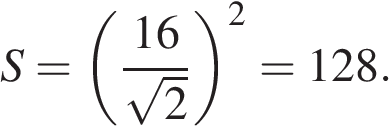
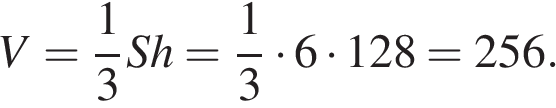
 В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы. . Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
. Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем .
. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен  , а высота равна 2.
, а высота равна 2. . Площадь боковой поверхности призмы тогда равна
. Площадь боковой поверхности призмы тогда равна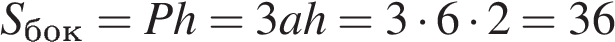 .
. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.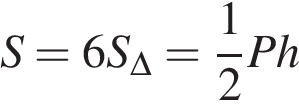 ,
, – периметр основания, а
– периметр основания, а  . Тогда площадь боковой поверхности
. Тогда площадь боковой поверхности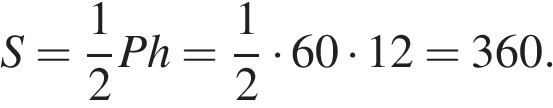
 Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на
Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на  . Площадь полной поверхности конуса
. Площадь полной поверхности конуса .
. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. .
. Объем шара равен 288
Объем шара равен 288 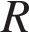 вычисляется по формуле
вычисляется по формуле 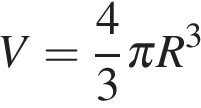 , откуда
, откуда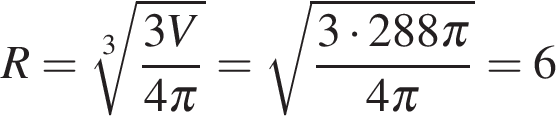 .
.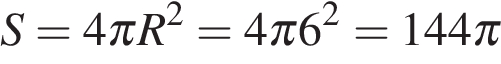 .
. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны  Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. :
: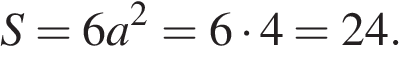
 Найдите объем
Найдите объем  .
. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен  .
.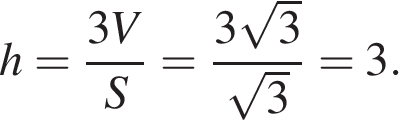
 .
.


