Решение. 16 страница
Тогда объем
Ответ: 1. Ответ: 1 3. B 13. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1: 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. Решение.
Ответ: 10. Ответ: 10 4. B 13. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3. Решение. Площадь лежащего в основании пирамиды многоугольника является разностью площадей квадратов со сторонами 6 и 3 (см. рис.):
Поскольку высота пирамиды равна 3, имеем:
Ответ: 27. Ответ: 27 B 13.
Решение. Площадь осевого сечения цилиндра равна
Ответ: 4. Ответ: 4 6. B 13. Решение. Площадь основания равна
Из формулы для объема пирамиды найдем высоту:
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:
Ответ: 7. Ответ: 7 7. B 13. Решение. Площадь поверхности складывается из площади основания
Радиус основания найдем по теореме Пифагора для треугольника, образованного высотой, образующей и радиусом:
Ответ: 144. Ответ: 144 8. B 13. Решение. Радиус вписанного в куб шара равен половине длины ребра:
Ответ: 4,5. Ответ: 4,5 9. B 13. Решение. Площадь пирамиды равна
Площадь боковой стороны пирамиды
Ответ: 340. Ответ: 340 10. B 13. Вариант № 3713843 1. B 13. Решение. Объем шара радиуса
Площадь его поверхности:
Ответ: 144. Ответ: 144 2. B 13. Решение. Объем данной части конуса равен
Ответ: 607,5. Ответ: 607,5 3. B 13. Решение. рассмотрим прямоугольный треугольник
Угол между сторонами правильного шестиугольника равен
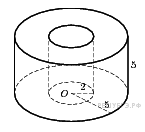
Значит, Ответ: 2. Ответ: 2 4. B 13. Решение. Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
Ответ: 105. Ответ: 105 5. B 13. Решение. Найдем третье ребро из выражения для объема:
Площадь поверхности параллелепипеда
Ответ: 22. Ответ: 22 6. B 13. Решение. Высота и сторона такого параллелепипеда равны диаметру сферы, то есть это куб со стороной 2. Площадь поверхности куба со стороной
Ответ: 24. Ответ: 24 7. B 13. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1: 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. Решение.
Ответ: 10. Ответ: 10 8. B 13. Решение. Обозначим известные ребра за
откуда неизвестное ребро
Диагональ параллелепипеда находится как
Ответ: 3. Ответ: 3 9. B 13. Решение. Сторона правильного шестиугольника
Ответ: 24. Ответ: 24 10. B 13. Решение. Обозначим известные ребра за
Диагональ параллелепипеда находится как
Выразим
Тогда площадь поверхности
Ответ: 64. Ответ: 64
Вариант № 3713899 1. B 13. Решение. Из условия
Ответ: 10. Ответ: 10 2. B 13. Решение. Пусть длина ребра куба равна а, а его диагональ равна d. Радиус описанного шара R равен половине диагонали куба:
Поэтому объем шара равен
Тогда
Ответ: 4,5. Ответ: 4,5 3. B 13. В прямоугольном параллелепипеде Решение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение
Из прямоугольного треугольника
Тогда площадь прямоугольника
Ответ:572. Ответ: 572 4. B 13. Решение. Объем прямоугольного параллелепипеда равен
Ответ: 8. Ответ: 8 5. B 13. Решение. Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме попарных произведений его измерений
Ответ: 22. Ответ: 22 6. B 13. Решение. Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
Ответ: 105. Ответ: 105 7. B 13. Решение. Площадь осевого сечения цилиндра равна
Ответ: 4. Ответ: 4 8. B 13. На Решение. Объем данной части конуса равен
Ответ: 216. Ответ: 216 9. B 13. Решение. Объем шара радиуса
Площадь его поверхности:
Ответ: 144. Ответ: 144 10. B 13. Решение. Диагональ квадрата в основании призмы
Ответ: 4. Ответ: 4
Вариант № 3714009 1. B 13. Решение. Объем данной части конуса равен
Ответ: 607,5. Ответ: 607,5 2. B 13. Решение. По теореме Пифагора найдем, что половина диагонали основания равна 8. Тогда диагональ основания равна 16, а сторона –
Тогда объем пирамиды
Ответ: 256. Ответ: 256 3. B 13. Решение. Длина диагонали параллелепипеда равна
Длина третьего ребра тогда
Ответ: 32. Ответ: 32 4. B 13. Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь Решение. Так как середина ребер куба является центром сферы, диаметр которой равен ребру куба, в кубе содержится 1/4 сферы и, соответственно, 1/4 ее поверхности. Имеем:
Ответ: 0,9025. Ответ: 0,9025 5. B 13. Решение. Площадь основания равна
Из формулы для объема пирамиды найдем высоту:
В правильном шестиугольнике сторона равна радиусу описанной окружности, поэтому найдем боковое ребро пирамиды по теореме Пифагора:
|

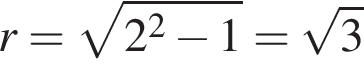 .
.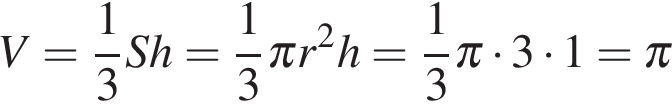 .
. При одинаковой площади основания большим объемом будет обладать та часть, высота которой больше, то есть нижняя. Объем данной пирамиды относится к объему исходной как
При одинаковой площади основания большим объемом будет обладать та часть, высота которой больше, то есть нижняя. Объем данной пирамиды относится к объему исходной как 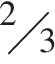 и поэтому равен 10.
и поэтому равен 10.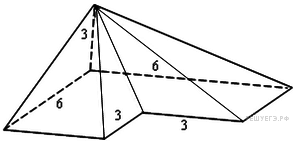
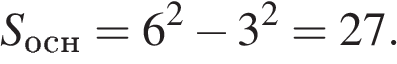
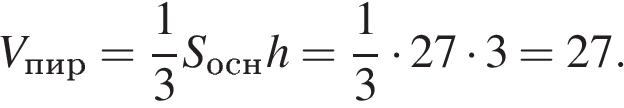
 Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на
Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на  .
.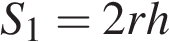 , так как это прямоугольник. Площадь боковой поверхности
, так как это прямоугольник. Площадь боковой поверхности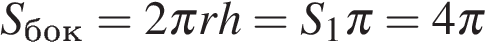 .
.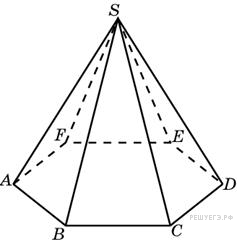 Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.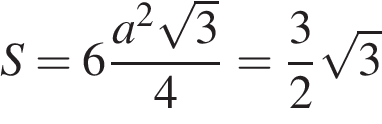 .
.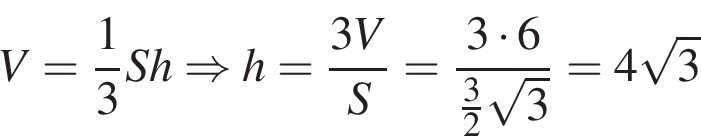 .
. .
. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на
Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на  и площади боковой поверхности:
и площади боковой поверхности: .
.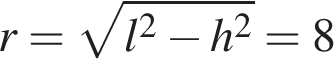 . Тогда площадь поверхности
. Тогда площадь поверхности
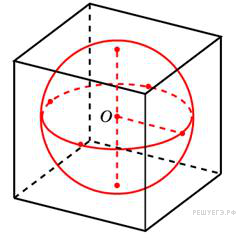 В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на  . Тогда объем шара
. Тогда объем шара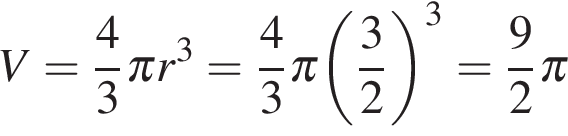 .
.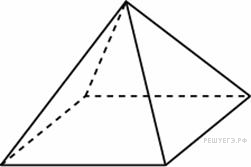 Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. .
. . Высоту треугольника
. Высоту треугольника  найдем по теореме Пифагора:
найдем по теореме Пифагора:  . Тогда площадь поверхности пирамиды
. Тогда площадь поверхности пирамиды .
.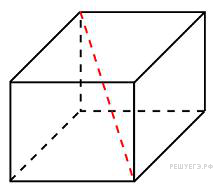 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.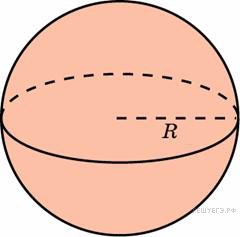 Объем шара равен 288
Объем шара равен 288 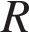 вычисляется по формуле
вычисляется по формуле 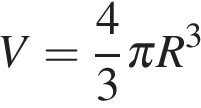 , откуда
, откуда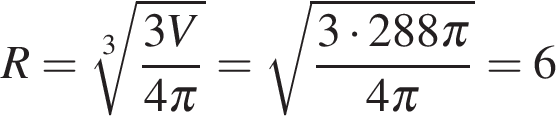 .
.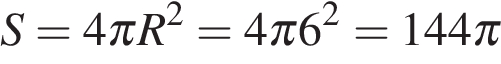 .
. Найдите объем
Найдите объем  части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите  .
. .
. В правильной шестиугольной призме
В правильной шестиугольной призме  все ребра равны 1. Найдите расстояние между точками
все ребра равны 1. Найдите расстояние между точками  и
и  .
.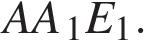 По теореме Пифагора
По теореме Пифагора
 По теореме косинусов
По теореме косинусов
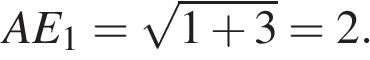
 Найдите объем
Найдите объем  .
. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности. .
.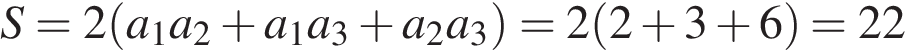 .
.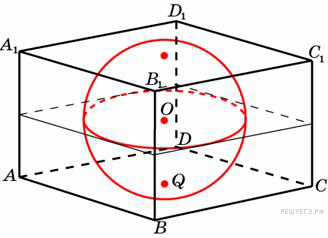 Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. :
: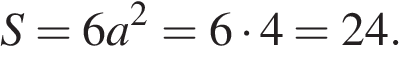
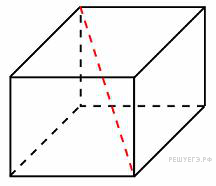 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.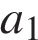 и
и  , а неизвестное за
, а неизвестное за 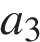 . Площадь поверхности параллелепипеда выражается как
. Площадь поверхности параллелепипеда выражается как  . Выразим
. Выразим 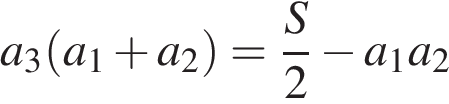 ,
,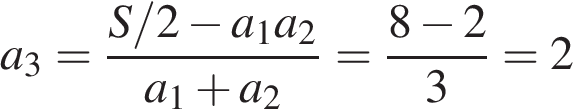 ,
, .
.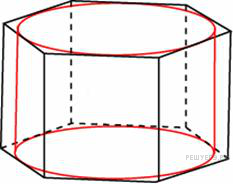 Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен  , а высота равна 2.
, а высота равна 2. выражается через радиус
выражается через радиус  вписанной в него окружности как
вписанной в него окружности как 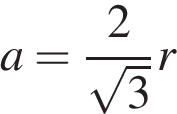 . Тогда площадь боковой поверхности призмы выражается формулой
. Тогда площадь боковой поверхности призмы выражается формулой .
. .
. .
.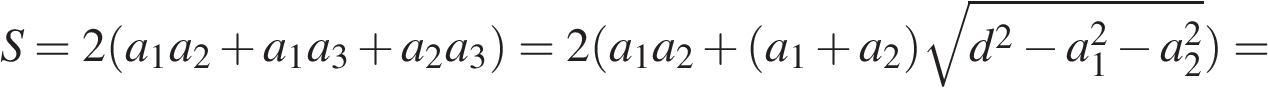

 Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.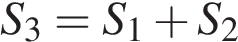 найдем, что радиус такого шара
найдем, что радиус такого шара .
.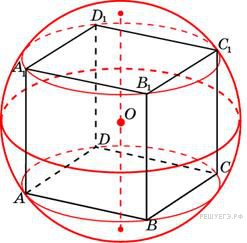 Около куба с ребром
Около куба с ребром 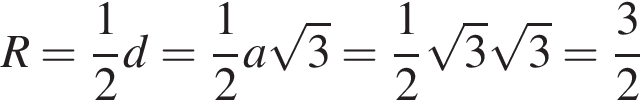 .
.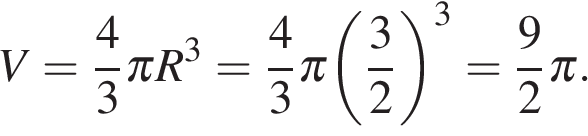
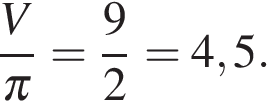
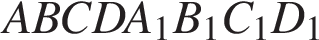 известны длины рёбер:
известны длины рёбер:  ,
, 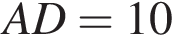 ,
,  . Найдите площадь сечения, проходящего через вершины
. Найдите площадь сечения, проходящего через вершины  и
и 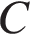 .
.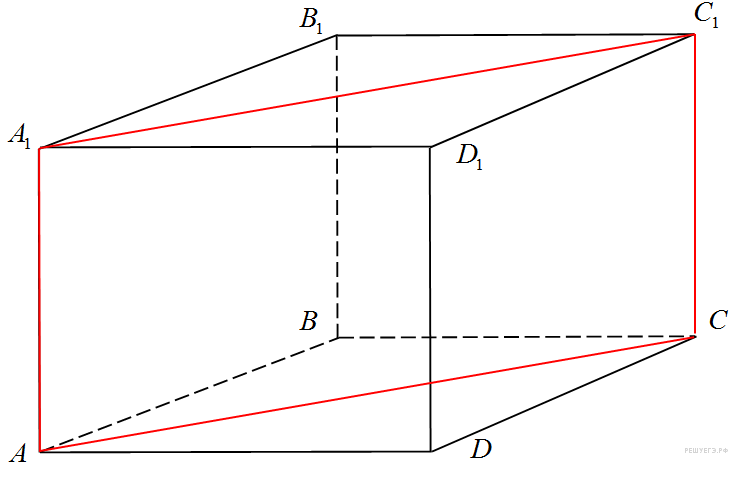
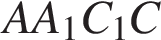 − параллелограмм. Кроме того, ребро
− параллелограмм. Кроме того, ребро 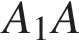 перпендикулярно граням
перпендикулярно граням  и
и 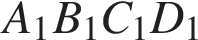 . Поэтому углы
. Поэтому углы 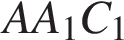 и
и 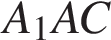 − прямые.Поэтому сечение
− прямые.Поэтому сечение  найдем
найдем 
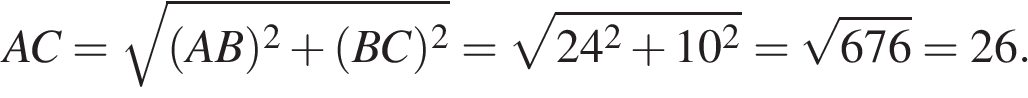

 Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.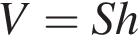 , где
, где  – площадь грани, а
– площадь грани, а  .
. .
.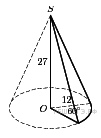 йдите объем
йдите объем 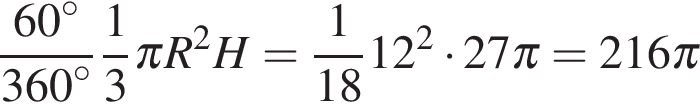 .
. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы.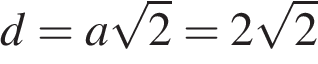 является диаметром описанного вокруг призмы цилиндра. Тогда его объем:
является диаметром описанного вокруг призмы цилиндра. Тогда его объем: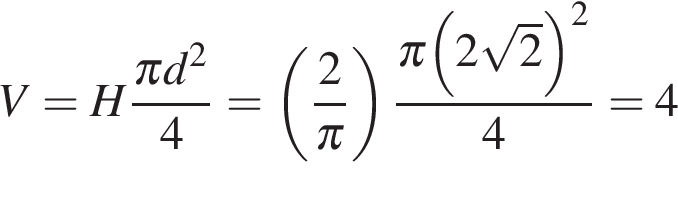 .
.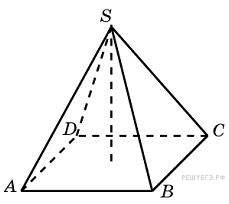 В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.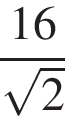 и площадь
и площадь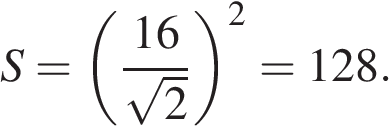
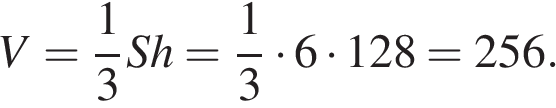
 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда. .
.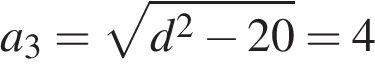 . Получим, что объем параллелепипеда
. Получим, что объем параллелепипеда .
. .
. .
.


