Решение. 18 страница
Решение. Рассмотрим прямоугольный треугольник
Ответ: 2. Ответ: 2 9. B 13. Решение. Площадь боковой поверхности пирамиды равна
где
Ответ: 360. Ответ: 360 10. B 13. В треугольнике, образованном радиусом основания r, высотой h и образующей конуса l, углы при образующей равны, поэтому высота конуса равна радиусу его основания: h = r. Тогда объем конуса, деленный на
Ответ: 9. Ответ: 9
Вариант № 3714834 1. B 14. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно? Решение. Обозначим объем бака за 1. Тогда три насоса, работая вместе, заполнят бак за
Ответ: 10. Приведем другое решение. Первый насос за минуту наполняет одну двадцатую бака, второй — одну тридцатую, третий — одну шестидесятую. Работая вместе, за минуту они наполнят шесть шестидесятых или одну десятую бака. Значит, весь бак насосы наполнят за 10 минут.
Приведем другое решение. За один час первый насос наполнит 3 бака, второй — 2 бака, а третий — 1 бак. Работая вместе, за один час они 6 баков. Значит, один бак насосы наполнят в шесть раз быстрее, т. е. за 10 минут. Ответ: 10 2. B 14. Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Решение. Пусть масса первого сплава
Ответ: 9. Ответ: 9 3. B 14. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий? Решение. Обозначим
Таким образом, второй рабочий делает 10 деталей в час. Ответ: 10. Ответ: 10 4. B 14. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч. Решение. Пусть
А через 2 часа 20 минут после этого догнал первого. Таким образом,
Таким образом, Ответ: 25. Ответ: 25 5. B 14. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? Решение. Пусть x ч — время, прошедшее от начала движения до момента встречи пешеходов. Тогда к моменту их встречи тот, кто шёл медленнее, прошёл 2,5 x км, а тот, кто шёл быстрее, прошёл 4,4 км до опушки и ещё 3 x км в обратном направлении. Пешеходы встретились на одном и том же расстоянии от опушки, поэтому расстояние, которое ещё осталось пройти до опушки более медленному из них, равно расстоянию, на которое более быстрый от неё уже удалился. Следовательно, 4,4 − 2,5 х = 3 х − 4,4, откуда х = 1,6 ч, а искомое расстояние равно 2,5 · 1,8 = 4 км.
Приведем другое решение. Тот, кто идет быстрее, дойдет до опушки за 4,4: 3 = 22/15 часа. За это время тот, кто идет медленнее, пройдет 2,5 · 22/15 = 11/3 км и окажется на расстоянии 4,4 − 11/3 = 11/15 км от опушки. Далее они пойдут на встречу друг другу со скоростью сближения 5,5 км/час и преодолеют разделяющее их расстояние за (11/15): 5,5 = 2/15 часа. За это время медленно идущий пешеход пройдет еще 2,5 · 2/15 = 1/3 км и окажется на расстоянии 11/3 + 1/3 = 4 км от точки отправления. Ответ: 4. Ответ: 4 6. B 14. Из городов Решение. Автомобиль, выехавший из города
Ответ: 50. Ответ: 50 7. B 14. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. Решение. Пусть скорость второго автомобиля равна
Ответ: 59. Ответ: 59 8. B 14. Клиент А. сделал вклад в банке в размере 6200 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 682 рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам? Решение. Если в банк под
Тем самым, банк начислял 10 процентов годовых.
Ответ: 10. Ответ: 10 B 14. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Решение. Пусть вторая труба наполняет резервуар за x минут, а первая — за x + 6 минут. В одну минуту они наполняют соответственно
Далее можно решать полученное уравнение. Но можно заметить, что при положительных x функция, находящаяся в левой части уравнения, убывает. Поэтому очевидное решение уравнения Ответ: 6. Ответ: 6 10. B 14. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?
Вариант № 3714930 1. B 14. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? Решение. Виноград содержит 10% питательного вещества, а изюм — 95%. Поэтому 20 кг изюма содержат
Ответ: 190. Ответ: 190 2. B 14. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч. Решение. Скорость товарного поезда меньше, чем скорого на 750 м/мин или на
Пусть
Ответ: 45. Ответ: 45 3. B 14. Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой? Решение. Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой – 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до последней встречи часовая стрелка пройдет
Часовая стрелка пройдет 9 делений, что соответствует 9 часам или 540 минутам.
Ответ: 540.
По просьбам читателей помещаем общее решение. Скорость вращения часовой стрелки равна 0,5 градуса в минуту, а минутной — 6 градусов в минуту. Поэтому когда часы показывают время h часов m минут часовая стрелка повернута на 30 h + 0,5 m градусов, а минутная — на 6 m градусов относительно 12-часового деления. Пусть в первый раз стрелки встретятся через t 1 минут. Тогда если минутная стрелка еще не опережала часовую в течение текущего часа, то 6 m + 6 t 1 = 30 h + 0,5 m + 0,5 t 1, т. е. t 1 = (60 h − 11 m)/11 (*). В противоположном случае получаем уравнение 6 m + 6 t 1 = 30 h + 0,5 m + 0,5 t 1 + 360, откуда t 1 = (60 h − 11 m + 720)/11 (**). Пусть во второй раз стрелки встретятся через t 2 минут после первого, тогда 0,5 t 2 = 6 t 2 − 360, откуда t 2 = 720/11 (***). Это же верно для каждого следующего оборота. Поэтому для встречи с номером n из (*) и (**) с учетом (***) имеем соответственно: tn = (60 h − 11 m + 720(n − 1))/11 или tn = (60 h − 11 m + 720 n)/11. Ответ: 540 4. B 14. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах. Решение. Относительная скорость поездов равна
За 36 секунд один поезд проходит мимо другого, то есть вместе поезда преодолевают расстояние, равное сумме их длин:
поэтому длина скорого поезда Ответ: 300. Ответ: 300 5. B 14. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 128 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. Решение. Пусть велосипедист ехал из А в В со скоростью
Искомая скорость велосипедиста на обратном пути на 8 км/час больше, поэтому она равна 16 км/час.
Ответ: 16. Ответ: 16 6. B 14. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? Решение. Пусть
Таким образом, мотоциклисты поравняются через
Ответ: 20. Приведём другое решение. Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа. Ответ: 20 7. B 14. От пристани A к пристани B отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч. Решение. Пусть
Таким образом, скорость первого теплохода равна 20 км/ч. Ответ: 20. Ответ: 20 8. B 14. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч. Решение. Заметим, что время подъема составило 1 час 30 минут или 1,5 часа, а время спуска 1,25 часа. Пусть x км/ч — скорость движения пешехода на спуске, тогда х − 2 км/ч — скорость движения пешехода на подъеме, 1,25 х км — длина пути на спуске, 1,5(х − 2) км — длина пути на подъеме. Всего было пройдено 8 км, откуда имеем:
Тем самым, скорость пешехода на спуске была равна 4 км/ч.
Ответ: 4. Ответ: 4 9. B 14. Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? Решение. Концентрация раствора равна
Ответ: 17. Ответ: 17 10. B 14. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч?
Вариант № 3715059 1. B 14. Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше? Решение. Обозначим
Ответ: 13. Ответ: 13 2. B 14. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй – длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? Решение. пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
Пусть
Ответ: 6. Ответ: 6 3. B 14. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды? Решение. Скорость совместной работы насосов
Для того, чтобы перекачать 25 литров воды, понадобится
Ответ: 6. Ответ: 6
|

 катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:
катет которого является большей диагональю основания. Длина большей диагонали правильного шестиугольника равна его удвоенной стороне:  . Поскольку
. Поскольку  имеем:
имеем: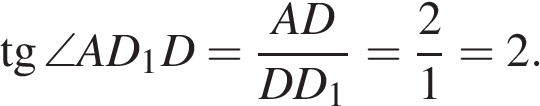
 Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.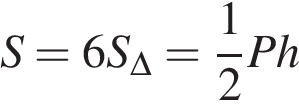 ,
, – периметр основания, а
– периметр основания, а 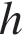 –апофема. Апофему найдем по теореме Пифагора:
–апофема. Апофему найдем по теореме Пифагора:  . Тогда площадь боковой поверхности
. Тогда площадь боковой поверхности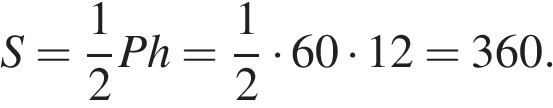
 Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на
Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на  . Решение.
. Решение.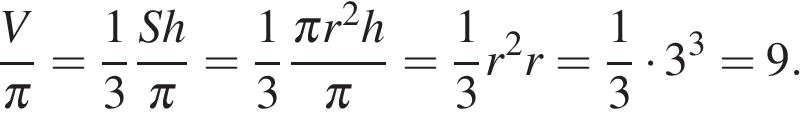
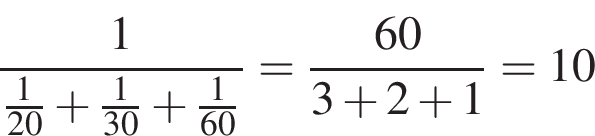 минут.
минут. кг, а масса второго –
кг, а масса второго –  кг, масса третьего сплава –
кг, масса третьего сплава –  кг. Первый сплав содержит 10% меди, второй – 40% меди, третий сплав – 30% меди. Тогда:
кг. Первый сплав содержит 10% меди, второй – 40% меди, третий сплав – 30% меди. Тогда:
 — число деталей, которые изготавливает за час второй рабочий. Тогда первый рабочий за час изготавливает
— число деталей, которые изготавливает за час второй рабочий. Тогда первый рабочий за час изготавливает  деталь. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей, отсюда имеем:
деталь. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей, отсюда имеем:
 .
.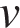 км/ч – скорость третьего велосипедиста, а
км/ч – скорость третьего велосипедиста, а 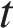 ч – время, которое понадобилось ему, чтобы догнать второго велосипедиста. Таким образом,
ч – время, которое понадобилось ему, чтобы догнать второго велосипедиста. Таким образом, .
.

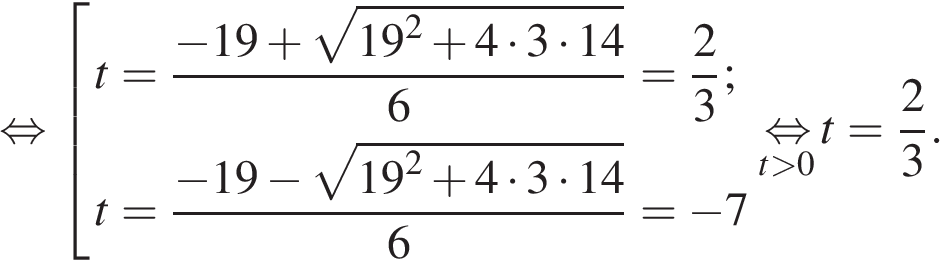
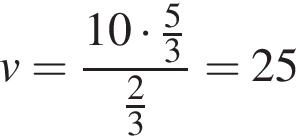 .
. и
и 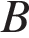 , расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города
, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города  км/ч.
км/ч. .
.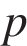 процентов годовых положена сумма
процентов годовых положена сумма  , то через
, то через  Поэтому клиент А. за два года получил
Поэтому клиент А. за два года получил  руб., а клиент B. за год получил
руб., а клиент B. за год получил  По условию,
По условию,  откуда имеем:
откуда имеем:

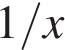 и
и  часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняеют одну четвертую часть резервуара:
часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняеют одну четвертую часть резервуара: .
. — единственно. Поскольку вторая труба заполняет
— единственно. Поскольку вторая труба заполняет  резервуара в минуту, она заполнит весь резервуар за 6 минут.
резервуара в минуту, она заполнит весь резервуар за 6 минут. кг питательного вещества. Таким образом, для получения 20 килограммов изюма требуется
кг питательного вещества. Таким образом, для получения 20 килограммов изюма требуется 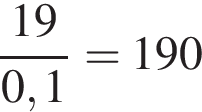 кг винограда.
кг винограда.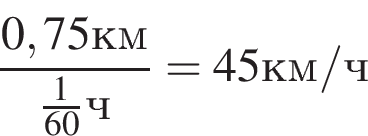 .
. км/ч. На путь в 180 км товарный поезд тратит времени на 2 часа больше, чем скорый, отсюда имеем:
км/ч. На путь в 180 км товарный поезд тратит времени на 2 часа больше, чем скорый, отсюда имеем: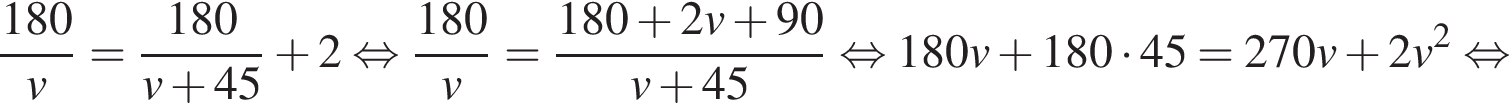
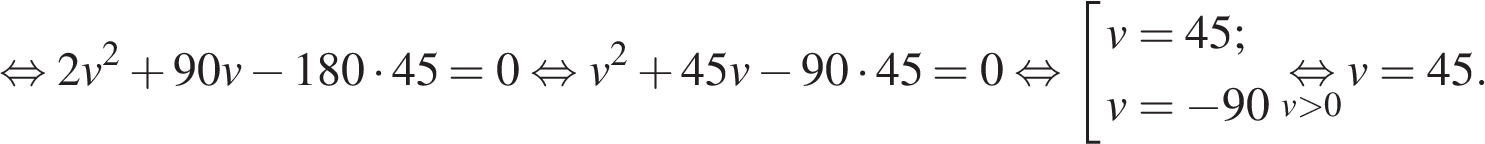
 делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок: .
.
 м,
м,
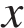 км/час, тогда обратно он ехал со скоростью
км/час, тогда обратно он ехал со скоростью  км/час. Разность времен на пути туда и обратно составляет 8 часов, откуда имеем:
км/час. Разность времен на пути туда и обратно составляет 8 часов, откуда имеем: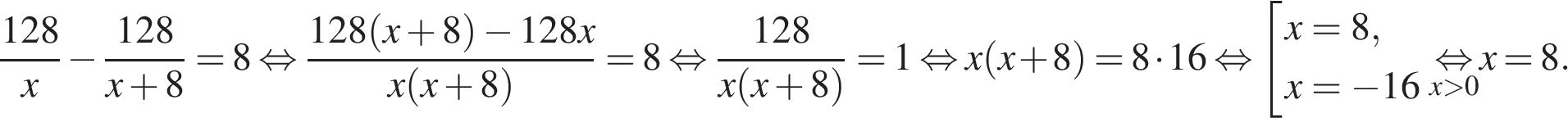
 км/ч. Пусть первый раз мотоциклисты поравняются через
км/ч. Пусть первый раз мотоциклисты поравняются через  .
. часа или через 20 минут.
часа или через 20 минут.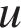 км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна
км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна  км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда имеем:
км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда имеем:
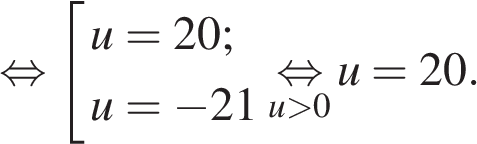
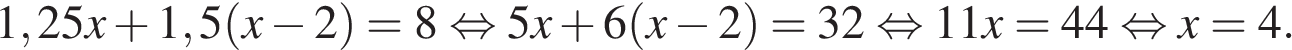
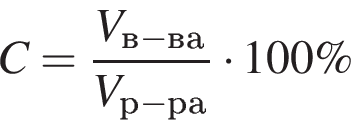 . Пусть объем получившегося раствора
. Пусть объем получившегося раствора  литров. Таким образом, концентрация полученного раствора равна:
литров. Таким образом, концентрация полученного раствора равна: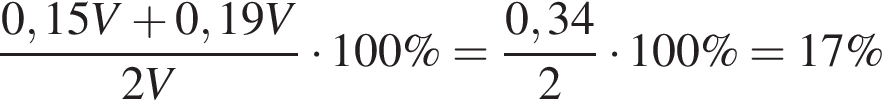
 деталь,
деталь,  . На изготовление 156 деталей первый рабочий тратит на 1 час меньше, чем второй рабочий, отсюда имеем:
. На изготовление 156 деталей первый рабочий тратит на 1 час меньше, чем второй рабочий, отсюда имеем:

 м.
м. м/мин
м/мин  км/ч
км/ч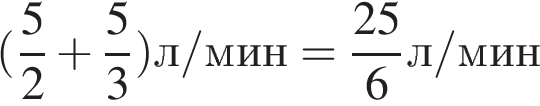 .
.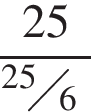 мин
мин 


