Структурная схема асинхронного электродвигателя, управляемого по цепи обмоток статора изменение напряжения.
составим структурную схему асинхронного двигателя, управляемого по цепи обмоток статора изменением напряжения. Если, в первом приближение, пренебречь влиянием электромагнитной инерций в цепях статора и ротора асинхронного двигателя, то структурную схему асинхронного двигателя можно найти из упрощенной формулы Клосса, представив ее в следующем виде:
Где
Подставив в (1) значение скольжения
Раскладывая полученное уравнение в ряд Тейлора в окрестности точки
Где
Структурная схема асинхронного двигателя, составленная по выражению
Рис. 15. Структурная схема асинхронного двигателя.
Рис.16. Упрощенная структурная схема асинхронного двигателя с учетом электромагнитной инерций. Линеаризованная структурная схема системы «тиристорный регулятор напряжения – асинхронный двигатель» (ТРН-АД) с отрицательной обратной связью по скорости, соответствующая функциональной схеме рис. 14 приведена на рис.17.
Рис.17. Структурная схема асинхронного электропривода с регулированием напряжения статора. На рис.17. приняты следующие обозначения:
В качестве расчетного значения коэффициента чувствительности по моменту Примем Разомкнутый контур скорости, настроенный на модульный оптимум, должен иметь следующую передаточную функцию:
где
Передаточная функция разомкнутого контура скорости рассматриваемой системы определяется следующим образом:
С целью упрощения решения задачи синтеза параметров регулятора скорости понизим порядок передаточной функции контура скорости. Для чего найдем суммарную малую постоянную времени
Приравнивая правые части выражений и решая полученное уравнение относительно передаточной функции регулятора скорости, получаем:
Если принять равным
Таким образом, при настройке контура скорости на модульный оптимум, регулятор скорости пропорционального типа с коэффициентом передачи Оценим в первом приближении устойчивость электропривода, выполненного в соответствии со структурной схемой, для чего найдем передаточную функцию замкнутой системы по управляющему воздействию:
где
Из критерия Льенара-Шипара для характеристического уравнения третьего порядка следует, что рассматриваемая система будут устойчивы при выполнение условия:
Система уравнений (11) справедлива для реальных параметров электроприводов, как для положительных, так и отрицательных значениях жесткости В тех случаях, когда электропривод с П-регулятором скорости не обеспечивает заданных показателей статической погрешности механических характеристик в принятом диапазоне регулирования скорости, контур скорости следует настраивать на симметричный оптимум. Разомкнутый контур скорости, настроенный на симметричный оптимум, должен иметь следующую передаточную функцию:
Где Передаточная функция разомкнутого контура скорости рис.2. с учетом суммарной малости постоянной времени определяется следующим уравнением:
После преобразований в итоге получаем:
Где
Графики переходных процессов момента и скорости электроприводов, настроенных на модульный и симметричный оптимум, определены для различных Механические характеристики электропривода ТРН-АД для задающих напряжений на рис. 22а. Анализ механических характеристик показывает, что погрешность поддержания скорости электропривода на нижней механической характеристике
Рис. 22а Механические характеристики электропривода ТРН-АД с П-регулятором скорости. В тех случаях, когда указанная погрешность не удовлетворяет требованиям технологического процесса, необходимо параметры регулятора скорости выбирать по симметричному оптимуму, то есть регулятор скорости должен быть пропорционально-интегральным.
|

 (1)
(1) - критический момент асинхронного двигателя при номинальном напряжение обмоток статора;
- критический момент асинхронного двигателя при номинальном напряжение обмоток статора;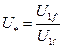 - относительное напряжение;
- относительное напряжение; , получим после преобразование
, получим после преобразование (2)
(2) , пренебрегая членами высшего порядка малости, можно получить
, пренебрегая членами высшего порядка малости, можно получить , (3)
, (3) - коэффициент чувствительности по моменту к изменению первой гармоники напряжения
- коэффициент чувствительности по моменту к изменению первой гармоники напряжения  ;
;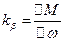 - жесткость механической характеристики асинхронного двигателя
- жесткость механической характеристики асинхронного двигателя  .
.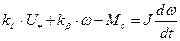 (4)
(4)


 - передаточная функция регулятора скорости;
- передаточная функция регулятора скорости; - коэффициент обратной связи по скорости,
- коэффициент обратной связи по скорости,  ;
; - коэффициент передачи датчика скорости,
- коэффициент передачи датчика скорости, 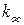 - коэффициент согласования, о.е.;
- коэффициент согласования, о.е.; - коэффициент передачи и постоянная времени тиристорного регулятора напряжения;
- коэффициент передачи и постоянная времени тиристорного регулятора напряжения; - момент инерции электропривода;
- момент инерции электропривода; принимаем его максимальное значение
принимаем его максимальное значение 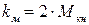 , при котором условия устойчивости контура регулирования скорости наихудшие.
, при котором условия устойчивости контура регулирования скорости наихудшие. , то есть механическая характеристика асинхронного двигателя в зоне регулирования скорости принимается абсолютно мягкой. Это допущение может быть приемлемым для синтеза параметров регулятора скорости, так как основной диапазон регулирования скорости расположен в зоне неустойчивых участков механических характеристик двигателя. Однако исследования переходных процессов необходимо производить с учетом максимального положительного значения
, то есть механическая характеристика асинхронного двигателя в зоне регулирования скорости принимается абсолютно мягкой. Это допущение может быть приемлемым для синтеза параметров регулятора скорости, так как основной диапазон регулирования скорости расположен в зоне неустойчивых участков механических характеристик двигателя. Однако исследования переходных процессов необходимо производить с учетом максимального положительного значения  , при котором условия устойчивости системы также наихудшие.
, при котором условия устойчивости системы также наихудшие.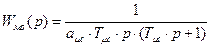 , (5)
, (5)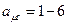 - коэффициент настройки на модульный оптимум контура скорости;
- коэффициент настройки на модульный оптимум контура скорости; - стандартный коэффициент настройки.
- стандартный коэффициент настройки. . (6)
. (6) , тогда преобразуется к виду
, тогда преобразуется к виду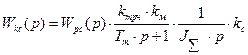 . (7)
. (7) . (8)
. (8) , то регулятор скорости будет иметь передаточную функцию:
, то регулятор скорости будет иметь передаточную функцию: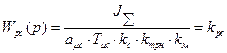 . (9)
. (9) .
. , (10)
, (10) ,
, - коэффициенты характеристического уравнения.
- коэффициенты характеристического уравнения. (11)
(11)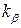 .
. (12)
(12) - коэффициент настройки контура скорости на симметричный оптимум;
- коэффициент настройки контура скорости на симметричный оптимум; 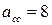 - стандартный коэффициент настройки.
- стандартный коэффициент настройки.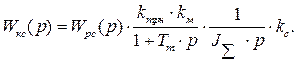 (13)
(13) (14)
(14) - коэффициент усиления регулятора скорости;
- коэффициент усиления регулятора скорости; - постоянная времени интегрирования регулятора скорости, с.
- постоянная времени интегрирования регулятора скорости, с.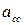 . Однако для асинхронного электропривода, имеющего участок механической характеристики с положительной жесткостью
. Однако для асинхронного электропривода, имеющего участок механической характеристики с положительной жесткостью  составляет
составляет 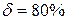 .
.



