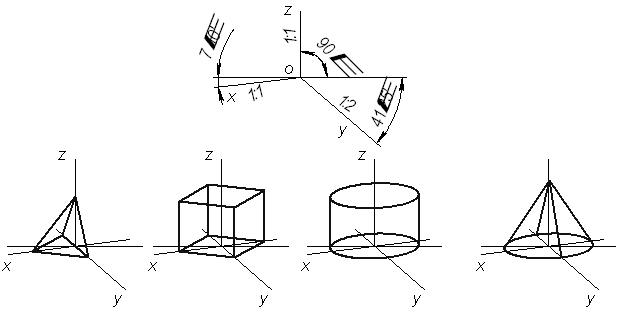
Прямоугольная диметрическая проекция.
Для каждой диметрической проекции исходным условием является равенство двух коэффициентов искажения. Рассмотрим случай, когда Стандарт (ГОСТ 2.317-69) рекомендует для практического применения прямоугольную диметрическую проекцию с показателем d = 0,5. Такому значению d соответствуют коэффициенты искажения k = n = 0,94 и m = 0,47 вычисленные по вышеуказанной формуле. Углы между аксонометрическими осями, а точнее угол Окружности, лежащие в плоскостях, параллельных плоскости координат П2, изображаются в виде эллипсов, большие полуоси которых равны R, а малые – 0,9R (рис. 9, б). В практике построения прямоугольных диметрических проекций рекомендуется пользоваться коэффициентами искажения k0=n0=1 и m0 =0,5.
Рис. 9. Прямоугольная диметрическая проекция: Изображения, построенные по этим коэффициентам, увеличиваются в 1,06 раз (1:0,94 = 1,06). По этой причине большие полуоси всех эллипсов, показанных на рис. 10, б становятся равными 1,06 R, а малые – 0,35 R (для окружностей, лежащих в плоскостях, параллельных П1 и П3) и 0,95 R (для окружностей лежащих в плоскостях, параллельных П2).
Рис.10.Примеры диметрических проекций геометрических тел
|

 . Если принять, что в этом случае m = dk и d есть некоторое положительное число. Назовем его показателем диметрии, то из основного уравнения
. Если принять, что в этом случае m = dk и d есть некоторое положительное число. Назовем его показателем диметрии, то из основного уравнения 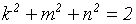 , которое примет вид
, которое примет вид  , можно получить формулы для вычисления коэффициентов искажения по заданному показателю диметрии:
, можно получить формулы для вычисления коэффициентов искажения по заданному показателю диметрии: ,
,  .
. и
и  , которые вычисляются по формулам
, которые вычисляются по формулам  и
и  . Расположение осей прямоугольной диметрической проекции на рис. 6, а.
. Расположение осей прямоугольной диметрической проекции на рис. 6, а.