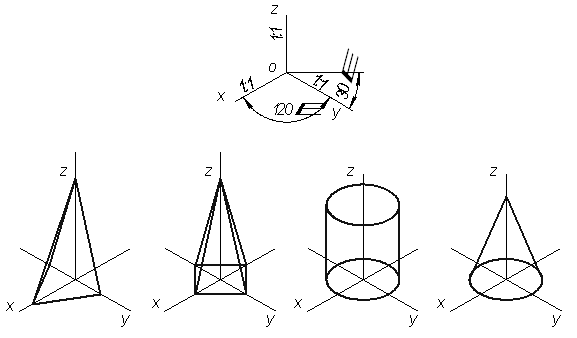
Прямоугольная изометрическая проекция. Коэффициент искажения в прямоугольной изометрии вычисляется по формуле , которая при k =m = n приобретает вид:
Коэффициент искажения в прямоугольной изометрии вычисляется по формуле Из теоремы о треугольнике следов говорится, что высоты треугольника следов совпадают с аксонометрическими осями системы, соответствующей данному треугольнику. Следовательно, углы между аксонометрическими осями в прямоугольной изометрической проекции одинаковые и равны 120о (рис. 4. а).
Рис. 4. Прямоугольная изометрическая проекция: а – расположение осей
Так как треугольник следов в прямоугольной изометрии равносторонний и высоты его пересекаются между собой под углом в 120о, то окружности, лежащие в плоскостях, параллельных координатным плоскостям, П1, П2 и П3, проецируются в виде эллипсов одинакового соотношения больших и малых осей (рис. 4, б). Большая полуось таких эллипсов равна радиусу R изображаемой окружности, а малая – 0,58 R. В практике построения прямоугольных изометрических проекций допускается применять не дробные действительные коэффициенты искажения k = m = n = 0,8, а округленные до единицы или, как их принято называть, приведенные коэффициенты искажения k0 = m0 = n0 = 1. Наглядное изображение, построенное по приведенным коэффициентам, увеличивается в 1,22 раза (1:0,82 = 1,22) по сравнению с действительным изображением, соответствующим коэффициентам искажения 0,82. При таком увеличении большие полуоси эллипсов, показанных на рис. 7, равны 1,22 R, а малые – 0,71 R. Прямоугольные изометрические проекции с действительными и приведенными коэффициентами искажения рекомендуются государственным стандартом (ГОСТ 2.317-69) для применения в техническом черчении.
Рис 5. Примеры изометрических проекций геометрических тел
|

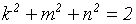 , которая при k =m = n приобретает вид:
, которая при k =m = n приобретает вид:  , откуда k = 0,82. Как видно, уравнение
, откуда k = 0,82. Как видно, уравнение