Решение модели
Подставим в уравнение рыночного спроса уравнение совокупного объема производства двух фирм и получим P=a-b(Q1+Q2). Выразим прибыли фирм как разность между совокупными доходами и совокупными издержками каждой из них: п1=TR1-TC1=PQ1-cQ1, п2=TR2-TC2=PQ2-cQ2, где с — средние краткосрочные издержки фирм (для простоты анализа издержки фирм приняты одинаковыми). Подставим в правые части полученных уравнений развернутое значение Р и получим п1={a-b(Q1+Q2)}Q1-cQ1=aQ1-bQ12-bQ2Q1-cQ1, п2={a-b(Q1+Q2)}Q2-cQ2=aQ2-bQ22-bQ2Q1-cQ2. Условие экономического равновесия предполагает невозможность прироста прибыли в точке оптимума или, другими словами, равенство предельной прибыли нулю: п1`(Q1)=0, п2`(Q2)=0, или
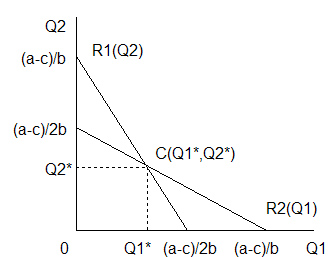
Перепишем эти уравнения следующим образом § a-2bQ1-bQ2-c=0, § § a-2bQ2-bQ1-c=0, § § 2bQ1=(a-c)-bQ2, § § 2bQ2=(a-c)-bQ1. Выразив объем выпуска одной фирмы через объем выпуска другой, уравнение кривых реакций дуополистов: Q1=(a-c)/2b — 0.5Q2, Q2=(a-c)/2b — 0.5Q1. Поскольку мы изначально рассматривали две схожие по издержкам и выпускаемой продукции фирмы, то их кривые реакции выражены одинаковыми уравнениями. Экономический смысл кривых реакции: Совокупность точек на кривой реакции показывает, какой будет реакция одной из фирм при выборе объема своего выпуска на решение другой фирмы относительно величины своего выпуска. Точка пересечения кривых реакции обоих дуополистов, совмещенных на единых координатных осях, называется точкой равновесия Курно. Графическое изображение данных кривых реагирования представлено на рис. 7.1.
На рис. 7.1 R1(Q2) — кривая реакции дуополиста 1 на величину выпуска, предложенного дуополистом 2, и соответственно R2(Q1) — кривая реакции дуополиста 2 на величину выпуска, предложенного дуополистом 1. Для того чтобы определить равновесные объемы выпусков обоих фирм, используем уравнения реакции. Подставим выражение Q2 в уравнение Q1=(a-c)/2b — 0,5Q2 и наоборот, и получим: Q1*=(a-c)/3b, Q2*=(a-c)/3b. В точке равновесия фирма 1 выбирает оптимальный для себя объем производства Q1*, предполагая, что ее конкурент поддерживает объем выпуска Q2*. В свою очередь, фирма 2 независимо от фирмы 1 выбирает оптимальный уже для нее объем Q2*, полагая выпуск своего конкурента равным Q1*. Таким образом никто из олигополистов не желает изменять своего выбора в одностороннем порядке. Как видно из полученного уравнения и рис. 7.1, равновесный совокупный объем выпуска обоих фирм, действующих независимо друг от друга, покрывает лишь 2/3 рыночного спроса, равного Q=(a-c)/b:
Очевидно, что если бы фирмы могли договориться о разделе рынка и действовали как единая монополия, то рынок был бы поделен пополам, и каждая из фирм обеспечивала бы лишь по 1/4 рыночного спроса, реализуя продукцию по более высоким ценам и получая соответственно более высокую прибыль. Доказательство. Совокупный доход обеих фирм равен Следовательно, предельный доход равен MR=a-2bQ. Совокупные издержки обоих фирм составляют TC=cQ. Соответственно, предельные издержки MC=c. Таким образом, приравняв предельные издержки к предельному доходу, мы получим оптимальный объем выпуска обоих фирм при согласованных действиях: § MC=MR, § § с=a-2bQ, § § 2bQ=a-c, § § Q=(a-c)/2b. Итак, на каждую фирму при делении рынка пополам пришлось бы по (a-c)/4b выпуска продукции.
|