Задачи для домашнего решения. №8. Записать уравнение окружности, если:
Окружность №8. Записать уравнение окружности, если: 1) центр в точке 2) центр в точке №9. Найти радиус окружности Эллипс №10. Составить каноническоеуравнение эллипса, если большая ось равна 10, а расстояние между фокусами равно 6. Построить эллипс. Гипербола №11. Дано уравнение гиперболы Парабола №12. Дано уравнение параболы координаты вершины параболы, точки пересечения параболы с осями координат. Построить параболу. №13. Построить кривые по заданным уравнениям: 1) 3) Ответы. 1. 1) х2 + у2 =16; 2) (х + 6)2 + (у - 8)2 = 100. 3.. 5.. 6. 1) 4; 3; 2) (-5; 0); (5; 0); 3), 7. 8. 1) (х -2)2 + (у + 1)2 = 4; 2) (х +1)2 + (у - 3)2 = 25. 9. 2; (-2; 0). 10.. 12. 1) 13.. Практическое занятие 11. Контрольная работа № 2 «Векторная алгебра и аналитическая геометрия» Вариант 0 Базовые задачи на оценку «удовлетворительно» Задача 1. Даны векторы 1) Записать координаты векторов 2) Построить векторы Задача 2. Найти для прямой Или: Задача 2. Для прямой Задача 3. Найти радиус окружности
Дополнительные задачи на оценку «хорошо», «отлично» (2-3 задачи на выбор студента) Задача 4. Найти координаты точки пересечения прямых Задача 5. Найти координаты вершины параболы
|

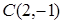 ,
,  ;
; , а окружность проходит через точку
, а окружность проходит через точку 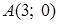 .
. , ее центр. Построить окружность.
, ее центр. Построить окружность. . Найти: 1) полуоси, 2) координаты фокусов, 3) записать уравнения асимптот.
. Найти: 1) полуоси, 2) координаты фокусов, 3) записать уравнения асимптот.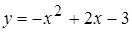 . Найти:
. Найти: , 2)
, 2)  ,
, , 4)
, 4)  .
. .
. ; (-2; -1).
; (-2; -1). ;
;  ; 2) (
; 2) ( ; 0); (
; 0); ( ; 0); 3)
; 0); 3)  .
. ,
, 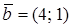 .
.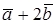 ,
,  .
. ,
,  ,
,  ,
,  1) угловой коэффициент, 2) координаты точек пересечения с осями Ох и ОУ. Построить прямую.
1) угловой коэффициент, 2) координаты точек пересечения с осями Ох и ОУ. Построить прямую. найти: 1) координаты нормального вектора, 2) координаты точек пересечения с осями Ох и ОУ. Построить прямую и нормальный вектор.
найти: 1) координаты нормального вектора, 2) координаты точек пересечения с осями Ох и ОУ. Построить прямую и нормальный вектор.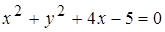 , ее центр. Построить окружность.
, ее центр. Построить окружность. и
и  . Построить прямые и проверить ответ.
. Построить прямые и проверить ответ. и точек пересечения параболы с осями координат. Построить параболу.
и точек пересечения параболы с осями координат. Построить параболу.


