Основные расчетные зависимости
РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ Особенности движения воды в открытых руслах Движение в открытых руслах является безнапорным и характеризуется тем, что все точки свободной поверхности потока находятся под одинаковым (атмосферным) давлением. Если в закрытом (напорном) потоке наличие местных сопротивлений вызывало изменение давления и не влекло изменение живого сечения во всем русле, то в открытом потоке всякое изменение условий движения (преграда, сужение или расширение потока, изменение уклона дна и т.д.) вызывает изменение живого сечения и, следовательно, координат свободной поверхности. Равномерное движение жидкости в открытом русле может иметь место лишь при определенных условиях: 1. Постоянство расхода; (Q= const) 2. Постоянство площади и формы живого сечения; (w = const) 3. Постоянство гидравлического уклона; (i = const) 4. Однотипность шероховатости смоченной поверхности по всей длине русла; (n =const) 5. Отсутствие местных сопротивлений. Следовательно, равномерное движение жидкости невозможно в естественных руслах, так как вдоль этих русел все гидравлические элементы потока изменяются. Равномерное движение жидкости может иметь место лишь в искусственых руслах (лотках, каналах), живые сечения, уклон, шероховатость которых вдоль потока остаются неизменными. Основные расчетные зависимости Основной формулой для расчета равномерного движения является формула Шези: В первой части курса были уже приведены формулы, следующие из зависимости:
где W и K - модуль расхода и модуль скорости соответственно. Учитывая (1) и (2), запишем:
Из приведенных выше формул следует:
Поскольку коэффициент Шези связан с коэффициентом Дарси соотношением:
а последний является функцией Re и же величин является и коэффициент Шези. В 1938 г. А.П. Зегжда опубликовал результаты экспериментов при исследовании им безнапорного потока в русле прямоугольного сечения. Полученные им результаты исследований были оформлены в виде графиков зависимости:
где R – гидравлический радиус, D - абсолютная шероховатость. Применение получила формула Агроскина:
С = 1/n + 17,72 lg R (1.7) Кроме этого применяются формулы Манинга и Форхгеймера:
Для практических расчетов следует рекомендовать: y = 1,5 y = 1,3 Существуют удобные таблицы и графики для определения коэффициента Шези по формулам Павловского, Манинга и Форхгеймера.
|

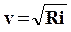 и
и 
 (1.1)
(1.1)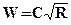 и
и 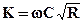 (1.2)
(1.2)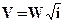 и
и 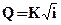 (1.3)
(1.3)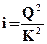 и
и  (1.4)
(1.4)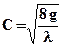 (1.5)
(1.5)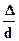 то очевидно, что функцией этих
то очевидно, что функцией этих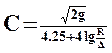 (1.6)
(1.6) и
и 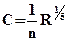 (1.8)
(1.8) Наиболее удачной считается формула академика Павловского:
Наиболее удачной считается формула академика Павловского: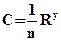 (1.9)
(1.9) при R < 1,0 м. (1.10)
при R < 1,0 м. (1.10)


