Гидравлически наивыгоднейший профиль каналов
Пусть заданы: расход Q = i = i.
Положим, что необходимо запроектировать поперечный профиль канала, то есть найти его размеры. Задача имеет много решений, так как можно наметить целый ряд профилей канала, удовлетворяющих заданным условиям. На расположенном ниже рисунке показаны три варианта профилей.Однако можно представить множество подобных вариантов, для которых:
Необходимая пропускная способность варианта а) обес- а) печивается большой шириной, для варианта в) - большой
ся большим смоченным периметром, то есть большой по- верхностью трения, поэтому скорость движения воды б) в них должна быть небольшой и, следовательно, среди
рого средняя скорость оказывается максимальной, а пло- щадь живого сечения минимальной.
Таким образом: “Гидравлически наивыгоднейшим профилем трапецеидального канала называется профиль, который при заданных Q, m, i, характеризуется максимально возможной средней скоростью v. Гидравлически наивыгоднейший профиль канала можно определить и следующим образом: Гидравлически наивыгоднейшим профилем трапецеидального канала является такой профиль, который при заданных w, m, i обеспечивает максимальную пропускную способность. Обозначим отношение Очевидно, что гидравлически наивыгоднейший профиль канала должен иметь минимальную площадь трения и, следовательно, минимальный смоченный периметр. Для того, чтобы найти соотношение размеров сечения канала, соответствующих гидравлически наивыгоднейшему профилю найдем производную от смоченного периметра по глубине и приравняем ее нулю:
и окончательно:
|

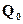 , форма поперечного сечения – трапецеидальная, коэффициент заложения откоса
, форма поперечного сечения – трапецеидальная, коэффициент заложения откоса 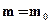 , уклон дна канала
, уклон дна канала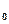
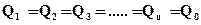 = const;
= const; 
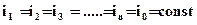






 глубиной. Первый и последний варианты характеризуют-
глубиной. Первый и последний варианты характеризуют-

 рассмотренных вариантов есть промежуточный, для кото-
рассмотренных вариантов есть промежуточный, для кото- в) Поперечный профиль, удовлетворяющий этим условиям является гидравлически наивыгоднейшим.
в) Поперечный профиль, удовлетворяющий этим условиям является гидравлически наивыгоднейшим.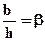 и назовем это выражение относительной шириной по дну.
и назовем это выражение относительной шириной по дну.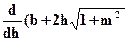 )= 0 подставив значение b из выражения w = h(b + mh), получим:
)= 0 подставив значение b из выражения w = h(b + mh), получим: 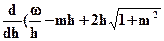 ) = 0 или
) = 0 или 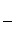
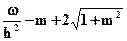 = 0, раскрывая w, получим:
= 0, раскрывая w, получим: 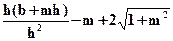 = 0 или -
= 0 или -  = 0;
= 0; =2(
=2( - m) (1.22)
- m) (1.22)


