Все элементы потока при глубине равной критической обозначаются с индексом «к». Таким образом в соответствии с уравнением (2.7):

 (2.8)
(2.8)





Из рассмотрения рис. 2.8 видно, что второй асимптотой кривой Э0 =f(h) будет прямая Э0 = h. Точка кривой, соответствующая ее минимуму, делит кривую на две ветви: нижняя отвечает такому состоянию потока, при котором с увеличением глубины происходит уменьшение удельной энергии сечения; верхняя – соответствует такому состоянию потока, при котором с увеличением глубины происходит увеличение удельной энергии сечения. Очевидно, что одним и тем же запасом энергии поток обладает при двух значениях глубин. График на рис 2.8 позволяет определить величину критической глубины hk, как глубины, соответствующей минимуму удельной энергии сечения. 
 Критическую глубину можно определить используя зависимость (2.8). Для этого необходимо задаться рядом значений h и подсчитав w, В и w3/В построим кривую w3/В = f(h), так как при Э0 min отношение
Критическую глубину можно определить используя зависимость (2.8). Для этого необходимо задаться рядом значений h и подсчитав w, В и w3/В построим кривую w3/В = f(h), так как при Э0 min отношение  ,то отложив по оси абсцисс величину
,то отложив по оси абсцисс величину  , получаем кривую
, получаем кривую 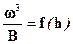 . Так как при Э0 min отношение
. Так как при Э0 min отношение 

справедливо, то отложив по оси абсцисс величину  , получаем на оси ординат hk (см. рис 2.9). Уравнение (2.8) не содержит ни уклона русла, ни его шероховатости, Следовательно критическая глубина определяется только расходом русла и его формой. Для определения критической глубины можно пользоваться графиком А.Н.Рахманова.
, получаем на оси ординат hk (см. рис 2.9). Уравнение (2.8) не содержит ни уклона русла, ни его шероховатости, Следовательно критическая глубина определяется только расходом русла и его формой. Для определения критической глубины можно пользоваться графиком А.Н.Рахманова.
При определении hk прямоугольных, треугольных, параболических русел графики не нужны, так как аналитическое определение критической глу
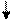 бины осуществляется достаточно просто
бины осуществляется достаточно просто
1. Прямоугльное русло: вводя в рассмотрение
удельный расход, преобразуем уравнение (2.8)
следующим образом:
 (2.9)
(2.9)
При a = 1,1 получим: hk = 0,482 q2/3;
При a = 1,0 получим hr = 0,467 q2/3;
Так как для прямоугольного русла q = Vk hk, то из формулы (2.9) следует:
 а отсюда следует:
а отсюда следует:
 (2.10)
(2.10)
Для параболическогорусла  при a = 1,0 (2.11)
при a = 1,0 (2.11)
 при a = 1,1 (2,12)
при a = 1,1 (2,12)
Для треугольного русла:  при a=1,1 (2.13)
при a=1,1 (2.13)
Для трапецеидальных русел критическую глубину можно определить, используя метод Агроскина: сначала вычисляем критическую глубину для условного прямоугольного русла:

 где Q – расход русла; b – ширина по дну данного русла. Затем находим значение величины
где Q – расход русла; b – ширина по дну данного русла. Затем находим значение величины  (2.14)
(2.14)
где m – коэффициент откоса данного русла.
Далее, пользуясь приближенной формулой (2.16) или таблицей находим особое значение функции f(sп), после чего вычисляем искомую критическую глубину данного трапецеидального русла:
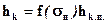 (2.15)
(2.15)
где: 
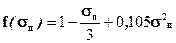 (2.16)
(2.16)


 (2.8)
(2.8)


 ,то отложив по оси абсцисс величину
,то отложив по оси абсцисс величину  , получаем кривую
, получаем кривую 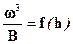 . Так как при Э0 min отношение
. Так как при Э0 min отношение 
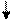 бины осуществляется достаточно просто
бины осуществляется достаточно просто (2.9)
(2.9) а отсюда следует:
а отсюда следует: (2.10)
(2.10) при a = 1,0 (2.11)
при a = 1,0 (2.11) при a = 1,1 (2,12)
при a = 1,1 (2,12) при a=1,1 (2.13)
при a=1,1 (2.13)
 где Q – расход русла; b – ширина по дну данного русла. Затем находим значение величины
где Q – расход русла; b – ширина по дну данного русла. Затем находим значение величины  (2.14)
(2.14)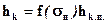 (2.15)
(2.15)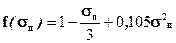 (2.16)
(2.16)


