Неравномерного плавноизменяющегося движения воды
Некоторые дополнительные замечания к неравномерному движению воды в открытых руслах В инженерной практике равномерное движение воды встречается чрезвычайно редко. Оно может иметь место лишь в искусственных водотоках с постоянным по форме и размерам профилем поперечного сечения, однообразной шероховатостью и уклоном дна. В естественных руслах и руслах с гидротехническими сооружениями эти условия никогда не выполняются. Любая преграда, выполненная в русле (плотина, мост и т.д.), любые неровности дна, изменение уклона вызывают неравномерное движение воды. Искусственные сооружения, возводимые на каналах всегда сопровождаются такими участками канала (переходами), где равномерное движение воды с физической точки зрения просто невозможно (русло с переменной шириной по дну, с горизонтальным дном, с обратным уклоном дна и т.д.)
При неравномерном движении наблюдается или изменение средней скорости потока или перераспределение скоростей по живому сечению потока, что обуславливает появление сил инерции и нарушает равновесие сил.
Стремление многочисленных исследователей описать математически неравномерное движение привело к выводу основного уравнение неравномерного плавноизменяющегося движения воды в открытых руслах, основанному на уравнении Бернулли. Запишем уравнение Бернулли для двух сечений, расположенных на расстоянии ds друг от друга (рис. 2.12):
Здесь ро – давление на свободной поверхности потока. dh - член, учитывающий потери напора на преодоление гидравлического сопротивления между сечениями, для которых записано уравнение Бернулли. После сокращений уравнение (2.28) примет вид
Обозначим Потери напора складываются из потерь напора на трение и потерь напора на преодоление местных сопротивлений: dh = dhм + dhтр и уравнение (2.30 может быть представлено в следующем виде: - dz = dhv + dhм + dhтр (2.31) Следует заметить: что потери напора на преодоление местных сопротивлений обусловлены изменением живого сечения по длине потока. Но так как изменение живого сечения в искусственных руслах осуществляется весьма медленно, то потери напора на преодоление местных сопротивлений по сравнению с потерями напора на трение весьма малы и ими чаще всего пренебрегают. Полагая в уравнении (2.31) dhм = 0, получаем более простое уравнение, которое обычно и применяется при рассмотрении неравномерного движения воды в открытых руслах. - dz = dhv + dhтр (2.32) Приведем это уравнение к виду, удобному для расчетов, для чего разделим обе его части на ds:
При этом необходимо заметить, что в отличие от равномерного движения гидравлические элементы потока V, C, R здесь переменные по длине потока. Тогда уравнение (2.33) с учетом (2.29) и (2.34) можно записать в следующем виде:
Заменив скорость V расходом Q, учитывая, что
где К – модуль расхода. Таким образом основное дифференциальное уравнение неравномерного плавноизменяющегося движение воды в открытых руслах можно записать либо в форме (2.35) либо в форме (2.36). Преобразуем последнее уравнение, введя в него глубину потока h. Пусть расход потока задан. Кроме того, будем считать заданной форму русла, так что все гидравлические элементы потока (w, c, R…) будем рассматривать, как непрерывные функции глубины потока h. Сначала установим связь между пьезометрическим уклоном I, глубиной потока h и уклоном дна русла i в данном сечении. Из рассмотрения рисунка 2.13 видно, что для произвольно выбранного сечения х-х, отстоящего от начального сечения О-О на расстоянии S, можно написать: z = a + h – is (2.37)
1. При равномерном движении глубина вдоль потока остается постоянной, то есть 2. При кривой подпора глубина вниз по течению повышается, то есть 3. При кривой спада глубина вниз по течению уменьшается Выполним дифференцирование правой части уравнения (2.36):, предполагая, что русло является непризматическим, то есть w = f (h, s)
Принимая во внимание уравнение (2.40), уравнение (2.36) запишется так:
В случае равномерного движения Решим уравнение (2.41) относительно
С учетом того, что K2 = w2C 2 R, уравнение (2.42) примет вид:
Уравнение (2.43) и является уравнением неравномерного плавноизменяющегося движения воды в открытых руслах, определяющее зависимость глубины потока от расстояния от начального сечения.
|

 Пусть живое сечение потока стеснено устоями моста. Для того, чтобы уменьшенное сечение потока могло пропустить заданный расход, средняя скорость в пределах сооружения должна увеличиваться, что, в свою очередь должно потребовать некоторого повышения свободной поверхности потока и, следовательно, уменьшения скорости течения перед мостом. Таким образом, перед мостом будет наблюдаться замедленное движение потока, которое переходит затем в ускоренное, а после моста снова становится замедленным. Равномерное движение характеризуется неизменностью гидравлических элементов по длине потока и, с позиций механики требует равновесия всех сил, действующих на какой-либо элемент потока, так как при равномерном движении живая сила остается постоянной по длине потока, а работа сил трения на данном перемещении должна быть равна работе остальных действующих сил на соответствующих перемещениях.
Пусть живое сечение потока стеснено устоями моста. Для того, чтобы уменьшенное сечение потока могло пропустить заданный расход, средняя скорость в пределах сооружения должна увеличиваться, что, в свою очередь должно потребовать некоторого повышения свободной поверхности потока и, следовательно, уменьшения скорости течения перед мостом. Таким образом, перед мостом будет наблюдаться замедленное движение потока, которое переходит затем в ускоренное, а после моста снова становится замедленным. Равномерное движение характеризуется неизменностью гидравлических элементов по длине потока и, с позиций механики требует равновесия всех сил, действующих на какой-либо элемент потока, так как при равномерном движении живая сила остается постоянной по длине потока, а работа сил трения на данном перемещении должна быть равна работе остальных действующих сил на соответствующих перемещениях.








 (2.28)
(2.28) или, пренебрегая бесконечно малой величиной второго порядка, получим:
или, пренебрегая бесконечно малой величиной второго порядка, получим: (2.29)
(2.29) , тогда – dz=dhv+dh (2.30)
, тогда – dz=dhv+dh (2.30) (2.33)
(2.33) где
где  - пьезометрический уклон (уклон свободной поверхности в данном сечении). Знак (-) означает, что понижению свободной поверхности потока, то есть уменьшению координаты z соответствует положительное значение пьезометрического уклона.
- пьезометрический уклон (уклон свободной поверхности в данном сечении). Знак (-) означает, что понижению свободной поверхности потока, то есть уменьшению координаты z соответствует положительное значение пьезометрического уклона. = if - гидравлический уклон, то есть потери напора на единицу длины потока:
= if - гидравлический уклон, то есть потери напора на единицу длины потока:  (2.34)
(2.34) (2.35)
(2.35) , получим:
, получим: , то
, то (2.36)
(2.36)





 (2.38)
так как
(2.38)
так как  , то
, то
 (2.39)
Эта зависимость играет важное значение при изучении неравномерного двжения воды в открытых руслах.
(2.39)
Эта зависимость играет важное значение при изучении неравномерного двжения воды в открытых руслах.
 и I = i – уклон свободной поверхности (пьезометрический уклон) равен уклону дна.
и I = i – уклон свободной поверхности (пьезометрический уклон) равен уклону дна. - величина положительная, в силу чего I < i, то есть уклон свободной поверхности меньше уклона дна.
- величина положительная, в силу чего I < i, то есть уклон свободной поверхности меньше уклона дна. - величина отрицательная, вследствие чего I > i,
- величина отрицательная, вследствие чего I > i, Учитывая, что
Учитывая, что  , получим:
, получим: (2.40)
(2.40) (2.41)
(2.41) и тогда
и тогда  то есть уравнение (2.41) обращается в уравнение равномерного движения.
то есть уравнение (2.41) обращается в уравнение равномерного движения. :
: откуда:
откуда:  (2.42)
(2.42)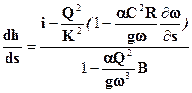 (2.43)
(2.43)


