Удельная энергия сечения. Критическая глубина.
Удельной энергией сечения Э0 называется частной значение полной удельной энергии потока, определенное относительно плоскости сравнения,.проходящей через наинизшую точку сечения русла. При плавноизменяющемся течении пьезометрический напор z +p/g одинаков во всех точках живого сечения. Для указанной плоскости сравнения имеем z + p/g =h и, следовательно, вместо (2.1) имеем: Э0 = h + aV2/2g (2.2) или Э0 = h + aQ2/2g w2 (2.3) Для прямоугольного русла используется понятие удельного или единичного расхода:
где Q/b – называется удельным или единичным расходом. Уравнения (2.2) и (2.3) показывают зависимость удельной энергии сечения от глубины при постоянном расходе. При увеличении глубины потока h первый член уравнения (2.3), представляющий собой величину удельной потенциальной энергии увеличивается, а второй член, представляющий величину удельной кинетической энергии уменьшается. Глубина потока при данном расходе может изменяться в пределах от 0 до ¥. Рассмотрим изменение удельной энергии сечения при этих колебаниях глубин. Для исследования изменения величины удельной энергии сечения в зависимости от изменения глубины h определим характер изменения функции Э0 = ¦(h), для чего возьмем первую производную от Э0 по h и приравняем ее нулю:
   Как видно из рис. (2.8), приращение живого сечения равно dw = Bdh Как видно из рис. (2.8), приращение живого сечения равно dw = Bdh
Где В – ширина зеркала воды при глубине h. Следовательно, с учетом (2.6):
Взяв вторую производную
|


 (2.1)
(2.1) (2.4)
(2.4) (2.5)
(2.5)


 При h 0 согласно (2.5) Э0 ¥. Следовательно, если построить кривую Э0 = f (h) в прямоугольных координатах, откладывая по оси ординат h, а по оси абсцисс Э0, то эта кривая асимптотически приближается к оси абсцисс. При h 0 удельная энергия Э0 ¥. Однако, здесь следует учесть, что с увеличением h резко возрастает w2 и поэтому при достаточно больших h уравнение (2.5) стремится к уравнению вида Э0 = h, то есть прямой, выходящей из начала координат под углом 450 . Функция Э0 = f(h) имеет экстремум, который находим, взяв производную
При h 0 согласно (2.5) Э0 ¥. Следовательно, если построить кривую Э0 = f (h) в прямоугольных координатах, откладывая по оси ординат h, а по оси абсцисс Э0, то эта кривая асимптотически приближается к оси абсцисс. При h 0 удельная энергия Э0 ¥. Однако, здесь следует учесть, что с увеличением h резко возрастает w2 и поэтому при достаточно больших h уравнение (2.5) стремится к уравнению вида Э0 = h, то есть прямой, выходящей из начала координат под углом 450 . Функция Э0 = f(h) имеет экстремум, который находим, взяв производную  и приравняв ее нулю:
и приравняв ее нулю: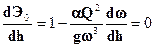 (2.6)
(2.6)


 Рис.2.7
Рис.2.7 (2.7)
(2.7) убеждаемся, что эта вторая производная больше нуля и, следовательно, функция Э0 = f(h) имеет минимум, а глубина,
убеждаемся, что эта вторая производная больше нуля и, следовательно, функция Э0 = f(h) имеет минимум, а глубина,


