Способ цепных подстановок
Сущность приема цепных подстановок заключается в последовательной замене базисной величины частных показателей, входящих в расчетную формулу, фактической величиной этих показателей и измерения влияния произведенной замены на изменение величины изучаемого обобщающего показателя. Пример. Есть функция y = a∙b∙c, необходимо рассчитать влияние факторов. Базовое значение обобщающего показателя: y0 = a0∙b0∙c0, (3.14) Фактическое значение обобщающего показателя: y1 = a1∙b1∙c1, (3.15) Скорректированные (условные) значения обобщающего показателя: Yусл 1 = a1∙b0∙c0, (3.16) Y усл 2 = a1∙b1∙c0, (3.17)
Отклонение обобщающего показателя за счет изменения факторов а, b, c:
∆ya = yусл1 – y0 = a1∙b0∙c0 – a0∙b0∙c0, (3.18) ∆yb = yусл2 – yусл 1 = a1∙b1∙c0 – a1∙b0∙c0, (3.19) ∆yc = y1 – yусл2 = a1∙b1∙c1 – a1∙b1∙c0, (3.20)
Общее отклонение обобщающего показателя (∆y)
∆y = y1 – y0 = a1∙b1∙c1 – a0∙b0∙c0, (3.21)
В итоге – общее отклонение должно быть равно сумме отклонений по факторам. Аналогичным образом этот метод используется в кратных и смешанных моделях.
Есть модель смешанного типа
Условные значения обобщающего показателя:
Отклонение обобщающего показателя за счет изменения факторов А, C, D:
Аналогично способ применяется во всех типах факторных моделей. Используя способ цепной подстановки необходимо придерживаться следующей последовательности расчетов: в первую очередь учитывают изменение количественных факторов, а затем качественных.
|
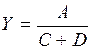, (3.22)
, (3.23)
, (3.24)
(3.25)
, (3.26)
, (3.27)
