Типы факторных моделей и их преобразование
В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами). При моделировании детерминированных факторных систем необходимо выполнять ряд требований: 1. Факторы, включаемые в модель и сами модели должны реально существовать, а не быть абстрактными. 2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. 3. Все показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность. 4. Сумма влияния отдельных факторов должна равняться общему приросту результативного показателя. В факторном анализе выделяют следующие наиболее часто встречающиеся типы факторных моделей: 1) аддитивные модели:
Они используются тогда, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей, например, показатель прибыли отчетного периода в зависимости от направлений ее получения. 2) мультипликативные модели:
Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов. 3) кратные модели:
Они применяются тогда, когда результативный показатель представляет собой соотношение факторов. 4) смешанные (комбинированные) модели – это сочетание различных вариантов предыдущих моделей.
Процесс моделирования факторных систем является сложным и ответственным моментом в анализе. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа. При построении детерминированных факторных моделей используют следующие основные приемы моделирования: 1) метод разложения одного из факторов:
Пример: Рентабельность активов:
где П – прибыль отчетного периода;
2) метод расширения факторной системы:
Пример: Среднегодовая выработка продукции одним работником:
где
3) метод сокращения факторной системы:
Пример: Фондоотдача основных средств:
где
В мультипликативных факторных системах моделирование осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов факторных моделей Выбор способа моделирования зависит от объекта исследования и от поставленной цели анализа.
|

 . (3.1)
. (3.1) . (3.2)
. (3.2) . (3.3)
. (3.3) ; (3.4)
; (3.4) ; (3.5)
; (3.5)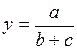 ; (3.6)
; (3.6) . (3.7)
. (3.7) . (3.8)
. (3.8) , (3.9)
, (3.9)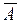 – среднегодовая стоимость активов предприятия;
– среднегодовая стоимость активов предприятия; – среднегодовая стоимость внеоборотных активов предприятия;
– среднегодовая стоимость внеоборотных активов предприятия; – среднегодовая стоимость оборотных активов предприятия.
– среднегодовая стоимость оборотных активов предприятия. . (3.10)
. (3.10)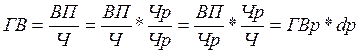 , (3.11)
, (3.11)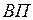 – стоимость выпущенной продукции за год;
– стоимость выпущенной продукции за год; – среднесписочная численность работников;
– среднесписочная численность работников; – среднесписочная численность рабочих;
– среднесписочная численность рабочих;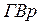 – среднегодовая выработка продукции одним рабочим;
– среднегодовая выработка продукции одним рабочим; – доля рабочих в составе работников.
– доля рабочих в составе работников. . (3.12)
. (3.12) , (3.13)
, (3.13) – среднегодовая стоимость основных средств предприятия;
– среднегодовая стоимость основных средств предприятия; – среднегодовая выработка продукции одним работником;
– среднегодовая выработка продукции одним работником;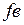 – фондовооруженность одного работника.
– фондовооруженность одного работника.


