Синтез систем управления.
Интересно отметить, что сам синтез систем управления осуществляется с использованием замкнутого контура обратной связи, как показано на рис. 1.1.9.
Рис. 1.1.9 Синтез системы управления – это уникальный пример технического проектирования. Цель проектирования состоит в определении конфигурации системы, требований, которым она должна удовлетворять, и задании основных параметров, удовлетворяющих предъявляемым к системе требованиям. Первый шаг процесса синтеза – это определение назначения системы. Например, поддержание заданного значения скорости вращения электродвигателя. Второй шаг – это указать те переменные, которые подлежат управлению (в нашем случае это скорость вращения). На третьем шаге мы должны предъявить требования к точности, с которой необходимо поддерживать скорость вращения электродвигателя. Последнее определяет выбор датчика, с помощью которого измеряется переменная, подлежащая управлению. Поставив себя на место инженера, первое, что мы должны сделать, – это попытаться создать конфигурацию системы, которая обладала бы желаемым качеством. Такая конфигурация обычно включает в себя датчик, объект управления, исполнительное устройство и регулятор, как показано на рис. 1.1.6. Следующий шаг состоит в выборе кандидата на роль исполнительного устройства. Принятие решения здесь зависит от типа объекта управления, но в любом случае выбранное устройство должно быть способно эффективно влиять на поведение объекта управления. Например, если мы хотим управлять скоростью вращения махового колеса, то в качестве исполнительного устройства нам надлежит выбрать электродвигатель. При этом датчик должен быть способен измерять скорость с высокой точностью. Наконец, мы должны получить модель для каждого из этих элементов. Следующий шаг состоит в выборе регулятора, который часто представляет собой сумматор, выполняющий операцию сравнения желаемого и действительного значений выходной переменной объекта, и следующий за ним усилитель сигнала ошибки. Заключительный шаг процедуры синтеза состоит в настройке параметров системы, которые обеспечивали бы желаемые показатели качества. Если в результате подбора параметров мы сможем достигнуть желаемого качества, то процесс синтеза на этом заканчивается и нам остается оформить рабочую документацию. В противном случае, возможно, потребуется заменить конфигурацию системы или выбрать исполнительное устройство и датчик с улучшенными характеристиками. После этого мы должны будем повторять все этапы синтеза до тех пор, пока не будут удовлетворены требования, предъявляемые к системе, или пока мы не решим, что эти требования являются слишком жесткими и их необходимо ослабить (см. рис. 1.1.9). Требования к качеству замкнутой системы управления должны затрагивать ее основные характеристики, к которым относятся: 1) хорошая компенсация возмущений, 2) желаемый вид реакции на задающее входное воздействие, 3) адекватные выходные сигналы исполнительного устройства, 4) малая чувствительность к изменению параметров и 5) робастность (устойчивость к возмущениям). На техническое проектирование сильное влияние оказало появление мощных и сравнительно недорогих компьютеров, а также высокопроизводительных программных средств анализа и синтеза систем управления. Например, самолет Боинг-777, оснащенный самой современной бортовой аппаратурой, был почти полностью спроектирован с помощью компьютерных технологий. Высокоточное компьютерное моделирование крайне важно для проверки результатов синтеза систем. Во многих случаях сертификация системы управления путем натурного моделирования требует значительных затрат времени и денег. Тот же Боинг-777 около 2400 раз был испытан с помощью компьютерного моделирования, прежде чем был построен первый самолет этой серии. Подводя итог, можно дать следующую формулировку задачи синтеза регулятора: дана модель объекта управления (вместе с датчиком и исполнительным устройством), а также установлены цели управления; требуется определить соответствующий регулятор, либо прийти к заключению, что таковой создать невозможно. 1.2. Математические модели физических систем. Для того чтобы изучить свойства сложной физической системы и научиться управлять ей, необходимо получить ее математическую модель. Для этого требуется установить все взаимосвязи между переменными, характеризующими поведение системы. Поскольку все реальные системы по своей природе являются динамическими, то для их описания естественно использовать дифференциальные уравнения. Если, кроме того, эти уравнения могут быть линеаризованы, то тогда можно воспользоваться преобразованием Лапласа. В действительности, сложность системы и игнорирование нами ряда привходящих факторов обуславливают возникновение некоторых допущений, связанных с функционированием данной системы. Поэтому часто бывает полезным игнорировать эти допущения и произвести линеаризацию системы. В результате на основании физических законов, описывающих поведение эквивалентной линейной системы, мы можем получить систему дифференциальных уравнений. Наконец, используя математический аппарат, такой как преобразование Лапласа, мы сможем получить решение, характеризующее поведение данной системы. В итоге алгоритм исследования динамики системы сводится к следующему: 1. Определить систему и ее компоненты. 2. Составить математическую модель и выдвинуть необходимые допущения. 3. Записать дифференциальные уравнения, описывающие поведение модели, 4. Решить уравнения относительно желаемых выходных переменных. 5. Проанализировать решения и допущения. 6. При необходимости провести повторный анализ или синтез системы. Дифференциальные уравнения непрерывных физических систем. Дифференциальные уравнения, описывающие динамику непрерывной физической системы, получаются на основании фундаментальных физических законов. Этот метод в равной степени применим к непрерывным системам различной физической природы. Например, с помощью закона Кирхгофа для токов можно описать электрическую RLC- цепь, представленную на рис. 2.1.1.
Рис. 2.1.1. В результате мы получим следующее интегро-дифференциальное уравнение uC (t) / R + C d uC (t)/d t + L -1 которое дифференцированием его левой и правой частей может быть сведено к дифференциальному уравнению второго порядка RC d2 uC (t)/d t 2+ d uC (t) /d t + RL -1 uC (t) = R i (t) (1.2.2) которое описывает динамику выходного параметра uC (t) (напряжение на емкости C) под воздействием входного возмущения i (t) – тока генератора. Принцип подобия. Дифференциальными уравнениями второго порядка с постоянными коэффициентами B d2 y (t) /d t 2 + C d y (t) /d t + D y (t) = x (t), (1.2.3) подобными (1.2.2), может быть описана динамика многих непрерывных механических, электрических, гидравлических и термодинамических систем. Наличие таких систем позволяет исследователю распространить решение, полученное для одной системы, на все подобные системы, описываемые аналогичными дифференциальными уравнениями. Следовательно, результаты, полученные, скажем, при анализе и синтезе электрических систем, сразу можно применить для представления о поведении гидравлических, тепловых и механических систем. Конечно-разностные уравнения дискретных физических систем. Используя современные компьютеры, дифференциальные уравнения можно решать численно, приводя их первоначально к т.н. конечно-разностному виду. Рассмотрим, например, дифференциальное уравнение третьего порядка с постоянными коэффициентами A, B, C и D A y ''' (t) + B y '' (t) + C y '(t) + D y (t) = x (t), (1.2.4) где y '(t) = d y (t) /d t. Приведем уравнение (1.2.4) к разностному виду, используя аппроксимацию производных конечными разностями для дискретных моментов времени, следующих через интервал D t y '(t) = [ y (t) – y (t – D t)] / D t – правая разность, y ''(t) = [ y (t+ D t) – 2 y (t) + y (t – D t)] / D t 2 – центральная разность, (1.2.5) y '''(t) = [ y (t+ D t) – 3 y (t) + 3 y (t – D t) – y (t – 2D t)] / D t 3 – правая разность. Перейдем к дискретному времени, где t = n D t, n = 0, 1, 2, …, N –дискретное время наблюдения; (1.2.6) D t ‑ дискретный интервал отсчетов. Тогда, подставляя 1.2.4 в 1.2.3, получим следующий вид конечно-разностного уравнения yn = a 1 yn- 1 + a2 yn- 2 + a 3 yn- 3 + xn, (1.2.7) где а yn = y (n D t) – «n»-ый отсчет переменной y, т.е. ее значение в момент времени t = n D t. Легко заметить, что конечно-разностное уравнение является частным случаем РАР-уравнения состояния ТП (1.1.2), рассмотренного в главе 1 (стр. 8) Модуля 1. Такие системы описывают дискретные физические системы, или физические системы дискретного времени. Линеаризация физических систем. Подавляющее большинство физических систем являются линейными лишь в некотором диапазоне изменения переменных. Однако при неограниченном возрастании этих переменных все системы я конечном счете становятся нелинейными. Систему можно определить как линейную, если воспользоваться действующим на нее возмущением и реакцией на это возмущение. В случае рассмотренной выше электрической цепи возмущением является входной ток I (t), а реакцией – напряжение UC (t). В общем случае необходимым условием линейности системы является соответствующая связь между возмущением x (t) и реакцией y (t). Если к системе, находящейся в состоянии покоя, приложить возмущение x 1(t), то на выходе появится реакция y 1(t). Если при тех же условиях подвергнуть систему возмущению x 2(t), то она даст соответствующую реакцию y 2(t). Необходимым условием линейности является то, чтобы при возмущении x 1(t) + x 2(t) система давала реакцию y 1(t) + y 2(t). Это положение обычно называют принципом суперпозиции. Кроме того, в линейной системе должен выполняться фактор масштабирования. Опять-таки будем считать, что входом системы является переменная x, а выходом – переменная y. Тогда необходимо, чтобы при умножении входной переменной на константу m реакция (выходная переменная) системы изменилась в такое же число раз, т.е. оказалась равна m y. Это свойство носит название гомогенности. Таким образом, линейная система удовлетворяет свойствам: суперпозиции и гомогенности. 1.3. Преобразование Лапласа и передаточные функции линейных систем. Преобразование Лапласа. Все физически реализуемые сигналы (функции) f (t) имеют преобразование Лапласа (образ Лапласа) F (s) =
|



 = i (t), (1.2.1)
= i (t), (1.2.1) ,
, 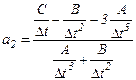 ,
,  , (1.2.8)
, (1.2.8) . (1.3.1)
. (1.3.1)


