Где o(s) есть полином системы, учитывающий начальные условия, а
q (s) = s n + q n-1 s n-1 +…+ q 0, (1.3.23) p (s) = p n-1 s n-1 + p n-2 s n-2 +…+ p 0. Если представить изображение по Лапласу входного возмущения дробно-рациональной функцией X (s) = то вместо (1.3.22) можно записать Y (s) = = Y 1(s) + Y 2(s) + Y 3(s). Обратное преобразование Лапласа дает y (t) = y 1(t) + y 2(t) + y 3(t), (1.3.25) где составляющие y 1(t) и y 2(t) обуславливают переходной процесс в системе, а составляющая y 3(t) – установившееся движение системы. Пример 1.3.5. Пусть нагревательная система, изображенная на рис. 1.3.3, имеет следующие параметры: T 1 – температура входного потока жидкости; T 2 – температура выходного потока жидкости; D T (s) = T 2 – T 1 – разность температур; С 0 – удельная теплоемкость воды; С 1 – теплоемкость жидкости; Q – расход жидкости; P (s) – тепловая мощность нагревательного элемента; R – тепловое сопротивление изоляции; G (s) – передаточная функция системы, задаваемая соотношением G (s) = Требуется найти время t переходного процесса системы – время остывания, а также вид динамики процесса.
Рис. 1.3.3 Решение. По аналогии с примером 1.3.2 преобразуем передаточную функцию системы к виду G (s) = где t = RC 1/(1+ RC 0 Q). Таким образом, динамика процесса остывания будет иметь вид D T (t) @ exp(- t / t). Структурные схемы. Для описания системы с несколькими управляемыми переменными используется структурная схема с перекрестными связями. Например, в системе на рис. 1.3.4 имеются две входных и две выходных переменных.
Рис. 1.3.4 С помощью передаточных функций можно связать выходы и входы Y 1(s) = G11 X 1(s) + G12 X 2(s), (1.3.27) Y 2(s) = G21 X 1(s) + G22 X 2(s), где G km – передаточная функция от m -го входа к k -му выходу. Структурная схема, отражающая зависимости (1.3.27) приведена на рис. 1.3.5.
Рис. 1.3.5
Методы преобразования структурных схем основаны на рассмотрении алгебраических соотношений между отдельными переменными. Например, рассмотрим структурную схему отрицательной обратной связи, изображенную на рис. 1.3.6.
Рис. 1.3.6. Очевидно, что E (s) = X (s) – Z (s) = X (s) – R (s) Y (s), Y (s) = G (s) E (s). Тогда Выражение (1.3.28) представляет собой передаточную функцию замкнутой системы регулирования. Структурные схемы дают гораздо лучшее представление о системах управления, чем описывающие их дифференциальные уравнения. Пример 1.3.6. Пусть замкнутая система регулирования имеет большой коэффициент усиления G (s) R (s) > 1. Тогда передаточная функция системы полностью определяется передаточной функцией R (s) обратной связи и не зависит от передаточной функции G (s) объекта управления
С другой стороны, если необходимо синтезировать такую передаточную функцию R (s) отрицательной обратной связи, чтобы выход системы всегда воспроизводил ее вход, т.е. Y (s) = = X (s), необходимо, как следует из (1.3.28), чтобы R (s) = 1–1/ G (s). (1.3.29) 1.4. Модели линейных систем в виде сигнальных графов. Для линейных систем достаточно сложной конфигурации Мейсоном предложен альтернативный метод взаимосвязи между переменными системы. Сигнальный граф представляет собой диаграмму, состоящую из узлов, соединенных между собой отдельными направленными ветвями. Например, сигнальный граф, соответствующий уравнениям (1.3.27) и структурной схеме рис. 1.3.5 изображен на рис. 1.4.1.
Рис. 1.4.1. Преобразование каждой переменной охарактеризовано надписью около направленной стрелки. Все ветви, выходящие из узла (кружок), передают сигнал другому (выходному) узлу каждой ветви. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную. Путь – это ветвь или последовательность ветвей, которые могут быть проведены от одного узла к другому. Контур – это замкнутый путь, который начинается и заканчивается в одном и том же узле, причем, вдоль этого пути ни один другой узел не встречается дважды. Некасающимися называются такие контуры, которые не имеют общего узла. Два касающихся контура имеют один или более общих узлов. Сигнальный граф – это просто наглядный метод записи системы алгебраических уравнений, показывающий взаимосвязь переменных. Например, рассмотрим следующую систему алгебраических уравнений a 11 x 1 + a 12 x 2 + u 1 = x 1, (1.4.1) a 21 x 1 + a 22 x 2 + u 2 = x 2.
Рис. 1.4.2. Записывая систему уравнений (1.4.1) в каноническом виде (1- a 11) x 1 - a 12 x 2 = u 1, (1.4.2) - a 21 x 1 + (1- a 22) x 2 = u 2 и решая ее по правилу Крамера, получим x 1 = x 2 = где определитель системы уравнений D = 1 – a 11 – a 22 – a 12 a 21 + a 11 a 22. (1.4.4) В данном случае определитель равен единице минус коэффициенты передачи a 11, a 22 и a 12 a 21 отдельных контуров плюс произведение коэффициентов передачи двух некасающихся контуров a 11 и a 22. Заметим, что контуры a 11 и a 21 a 12 являются касающимися, также как, как и контуры a 22 и a 12 a 21. В решении для x 1 по отношению ко входу u 1 числитель (1.4.3) равен значению определителя (1.4.4) не касающегося пути от u 1 к x 1. В решении для x 1 по отношению ко входу u 2 числитель (1.4.3) просто равен a 12, т.к. этот путь касается всех контуров. В общем случае передаточная функция П от входа X (s) к выходу Y (s) определяется формулой Мейсона
где П k – коэффициент передачи пути определяется как непрерывная последовательность ветвей, простирающихся в направлении, указанном стрелками, причем ни один узел не встречается в этой цепи более одного раза; D – определитель графа; Dk – дополнительный множитель определителя для k -го пути. Причем, D = 1 – (сумма коэффициентов передачи всех отдельных контуров) + (сумма произведений всех возможных комбинаций из 2 некасающихся контуров) – (сумма произведений всех возможных комбинаций из 3 некасающихся контуров) + …. Пример 1.4.1. На рис. 1.4.3 изображен сигнальный граф с двумя параллельными путями. Примером системы управления, граф которой имеет несколько путей, может служить распараллеленный конвейер. От входа X (s) к выходу Y (s) ведут следующие пути: путь 1 – П 1 = G 1 G 2 G 3 G 4 и путь 2 – П 2 = G 5 G 6 G 7 G 8.
Рис. 1.4.3 Граф содержит четыре контура: L 1 = G 2 R 2, L 2 = G 3 R 3, L 3 = G 6 R 6, L 4 = G 7 R 7. Так как контуры L 1 и L 2 не касаются контуров L 3 и L 4, то D = 1 – (L 1 + L 2 + L 3 + L 4) + (L 1 L 3 + L 1 L 4 + L 2 L 3 + L 2 L 4). Дополнительный множитель определителя для пути 1(2) вычисляется в результате удаления из D контуров, касающихся пути 1(2) D1 = 1 – (L 3 + L 4), D2 = 1 – (L 1 + L 2). Таким образом
Рис. 1.4.4 Прямые пути следующие: П1 = G 1 G 2 G 3 G 4 G 5 G 6, П2 = G 1 G 2 G 7 G 6, П3 = G 1 G 2 G 3 G 4 G 8. Кроме того имеются следующие контуры: L 1 = - G 2 G 3 G 4 G 5 G 6 R 2, L 2 = - G 5 G 6 R 1, L 3 = - G 8 R 1, L 4 = - G 7 R 2 G 2, L 5 = - G 4 R 4, L 6 = - G 1 G 2 G 3 G 4 G 5 G 6 R 3, = - G 1 G 2 G 7 G 6 R 3, L 8 = - G 1 G 2 G 3 G 4 G 8 R 3. Контур L 5 не касается контура L 4 или контура L 7; контур L 3 не касается контура L 4; все остальные контуры являются касающимися. Поэтому определитель графа: D = 1 – (L 1+ L 2+ L 3+ L 4+ L 5+ L 6+ L 7+ L 8) + (L 5 L 7+ L 5 L 4+ L 3 L 4). Дополнительные множители: D1 = D3 = 1 и D2= 1 – L 5 = 1 + G 4 R 4. Следовательно, 1.5. Законы регулирования и оценки качества. Рассмотрим систему автоматического регулирования, изображенную на рис. 1.5.1.
Рис. 1.5.1 Функциональная связь между выходной координатой регулятора u (t) (т.е. управляющим воздействием или положением регулирующего органа) и его входной координатой e (t) (т.е. отклонением действительного значения регулируемого параметра от заданного значения) называется законом (алгоритмом) регулирования. При этом рассматривается установившееся движение регулятора (после окончания затухающего переходного процесса, если он существует). У регуляторов плавного действия эти функциональные зависимости непрерывные и обычно линейные (часто прямая пропорциональность). Они могут включать в себя как сами координаты, так и их интегралы и производные. При этом пользуются следующими основными пятью законами регулирования. 1. По отклонению – управляющее воздействие пропорционально мгновенному значению отклонения (соответствующий регулятор по отклонению, или пропорциональный регулятор, или П-регулятор) u (t) = k e (t) = k [ y (t) – y э(t)], (1.5.1)
т.е. управляющее воздействие изменяется синхронно с отклонением (с постоянным коэффициентом k пропорциональности). Отсюда следует, что при неизменяющемся (постоянном) отклонении регулируемого параметра (e = e 0 = const) регулирующий орган неподвижен, т.е. не стремится устранить это отклонение. У рассматриваемого регулятора имеется прямая пропорциональность перемещения регулирующегося органа и вызывающегося его отклонение регулируемого параметра. В свою очередь, это отклонение также функционально связано с положением регулирующего органа. Поэтому любое отклонение нагрузки регулируемого объекта от заданного (номинального) значения потребует изменения положения регулирующего органа, т.е. появится u ¹ 0 (для компенсации этого возмущения по нагрузке), это в свою очередь в силу (1.5.1) приведет к тому, что и отклонение регулируемого параметра m ¹ 0. Следовательно, при регулировании по отклонению регулятор является статическим (часто называется пропорциональным вследствие пропорциональности его управляющего воздействия отклонению). Коэффициент пропорциональности, представляющий собой коэффициент усиления (передачи) регулятора, иногда называемый его чувствительностью, равен обратной величине статизма (или неравномерности) регулятора 2. По отклонению и производным – управляющее воздействие пропорционально мгновенному значению не только отклонения, но и производных (первой, второй) отклонения по времени (соответствующий регулятор по отклонению и производной, или пропорционально-дифференциальный, или ПД-регулятор)
Скорость регулирующего органа зависит не только от скорости изменения отклонения, но и от его второй производной (от ускорения). В том случае, когда отклонение регулируемого параметра еще только формируется (т.е. оно само и скорость его нарастания пока очень малы), но приложенное возмущение значительно, вторая производная отклонения по времени также значительна. Например, немедленно (t = 0) после приложения силы F к неподвижной массе m детали регулятора ее ускорение конечно и равно a = F / m, а скорость v = (at) t =0 и путь s = (at 2/2) t =0 еще равны нулю. Наоборот, при возникновении отрицательного ускорения начинается замедление нарастания регулируемого параметра. Это обстоятельство сейчас же будет учтено ПД-регулятором (уменьшением скорости регулирующего органа). Включение производной в закон регулирования позволяет регулирующему органу как бы предвидеть изменение регулируемого параметра. Такой регулятор работает, как говорят, с предварением и особенно целесообразен при резких и значительных возмущениях. При e = e 0 = const по-прежнему d e /d t = 0, т.е. отклонение не устраняется (регулятор статический). Как и в предыдущем случае П-регулятора, коэффициент k безразмерен и равен обратной величине статизма (неравномерности) регулятора. Коэффициент T д, как это видно из (1.5.2), имеет размерность времени и называется постоянной дифференциров ани я, или временем предварения. 3. По интегралу – управляющее воздействие пропорционально величине интеграла отклонения по времени (регулятор по интегралу, или интегральный регулятор, или И-регулятор)
Скорость регулирующего органа прямо пропорциональна отклонению регулируемого параметра. Очевидно, что регулирующий орган не может остановиться (при отсутствии зоны нечувствительности), пока имеется отклонение регулируемого параметра. Единственным достаточным и необходимым условием равновесия регулирующего органа является отсутствие отклонения регулируемого параметра лишь при e = 0 (значение d u /d t = 0 и u = const). Иначе говоря, при регулировании по интегралу регулятор стремится устранить (при t ® ∞) отклонение без статической ошибки (регулятор астатический). Коэффициент T И, как это нетрудно видеть из уравнения (I.5.3), имеет размерность времени и называется постоянной интегрирования регулятора. 4. По отклонению и интегралу – управляющее воздействие пропорционально величине не только отклонения, но и его интеграла по времени (регулятор по отклонению и интегралу, или пропорционально-интегральный регулятор, или ПИ-регулятор)
Здесь скорость регулирующего органа суммируется из двух слагаемых: одного, пропорционального скорости изменения отклонения регулируемого параметра, и другого, пропорционального самому отклонению. Единственным необходимым и достаточным условиям равновесия регулирующего органа (т.е. d u /d t = 0) является отсутствие отклонения регулируемого параметра (только когда e = 0 и d e /d t = 0). Следовательно, и в этом случае нет статической ошибки регулирования, и регулятор является астатическим изодромным (благодаря включению в закон регулирования самого отклонения). В (1.5.4) коэффициент k – безразмерный, а T И имеет размерность времени и называется временем изодрома регулятора (или постоянной интегрирования). 5. По отклонению, интегралу и производным – управляющее воздействие пропорционально величине отклонения, его интеграла и производных по времени (регулятор по отклонению, интегралу и производной или пропорционально-интегральный с производной, или пропорционально-интегральный дифференцирующий, или ПИД-регулятор)
Равновесие регулирующего органа наступит также лишь при e = 0, что связано с наличием в законе регулирования интеграла отклонения. В то же время наличие в этом законе производной отклонения создает работу регулятора с предварением. В итоге получается астатический изодромный регулятор с предварением. Таким образом, включение интеграла в закон регулирования всегда приводит к исключению статической ошибки регулирования (т.е. к астатичности регулятора), а включение в этот закон производной позволяет регулятору работать с предварением. В (I.5.5) участвуют все три коэффициента: k – безразмерный коэффициент усиления регулятора, с размерностью времени Т Д и ТИ. Для релейных регуляторов нет непрерывной функциональной зависимости u (e), для них чаще всего применяются рассмотренные далее два закона регулирования. Для релейного двухпозиционного регулятора (Рп-регулятора), у которого управляющее воздействие может иметь лишь два дискретных значения ± u 0,
где Зоной неоднозначности называется диапазон изменения входной координаты. Они зависят от направления изменения входной координаты и предшествующего состояния звена, системы и пр. Возникновение неоднозначности связано чаще всего с гистерезисом, наличием люфтов и т.п. Иначе говоря, при возрастании во времени отклонения e регулируемого параметра регулирующий орган срабатывает скачком (сменяет позицию): при e = +D значение – u 0 сменяется значением + u 0, а при обратном ходе e (его снижении) регулятор срабатывает при e = –D. У релейного регулятора постоянной скорости (Рс-регулятора)
т.е. регулирующий орган перемещается с постоянной скоростью, равной ±1/ T С, в одном или другом направлении, когда отклонение регулируемого параметра выходит в ту или иную сторону за зону нечувствительности. В ее пределах регулирующий орган находится в покое. Например, при срабатывании регулятора контактная система включает реверсивный электродвигатель регулирующего органа. Закон регулирования является важнейшей характеристикой регулятора, но не всегда описывает его поведение в динамике полностью, поскольку в левых частях уравнений этого закона фигурирует лишь одна величина – выходная координата. Во многих случаях при изменении выходной координаты нужно учитывать не одну, а две и больше величин (например, инерционные явления в регуляторе, т.е. перемещение и его скорость; перемещение, скорость и ускорение; скорость и ускорение и т.п.). Поэтому регулятор, поведение которого описывается уравнением закона регулирования, где участвует лишь одна величина, характеризующая выходную координату регулятора (без ее производных), называется идеальным. Иначе говоря, у идеального регулятора (как динамической системы) все постоянные времени в левой части уравнения динамики принимаются равным нулю (см. 1.5.4).
У П-регулятора выходная координата повторяет входную (в соответствующем масштабе). У ПД-регулятора координата u складывается из двух: одна повторяет входную координату (в соответствующем масштабе), а вторая пропорциональна производной e, т.е. в рассматриваемом случае (скачкообразное изменение e) в момент t = 0 координата u стремится к бесконечности, а ее длительность стремится к нулю. Следовательно, в момент образования (или увеличения) отклонения появляется дополнительное перемещение выходной координаты регулятора. У И-регулятора при e = const, очевидно, выходная координата возрастает линейно (интеграл постоянной величины с угловым коэффициентом У ПИ-регулятора для координаты u к наклонной прямой интеграла постоянной величины добавляется еще горизонтальная постоянная величина, пропорциональная уровню отклонения e = const. Поэтому по сравнению с графиком u (t) для И-регулятора в данном случае такая же наклонная прямая поднимается выше и при t = 0 выходит не из начала координат. Разность площадей под прямыми e (t) и u (t) до момента их пересечения меньше, чем у И-регулятора; величина перерегулирования также будет ниже и т.д. У ПИД-регулятора в отличие от ПИ-регулятора появляется дополнительный импульс при t = 0, как это показано ранее для ПД-регулятора. У Рп-регулятора зона неоднозначности ограничена петлей кусочно-линейной функции u (e). У Рс-регулятора выходная координата – скорость регулируемого органа – не зависит о направления изменения входного сигнала e и однозначно (кусочно-линейно) функционально связана со значением e. Качество регулирования. Оценка качества регулирования – это численный показатель или критерий качества системы регулирования, который выбирается так, чтобы подчеркнуть наиболее важное требование, предъявляемое к системе. Система считается оптимальной системой управле ния, если ее параметры выбраны таким образом, что оценка качества принимает экстремальное (обычно минимальное) значение. Одним из самых распространенных оценок качества может служить интеграл квадрата ошибка (ИКО) ИКО = Верхний предел интегрирования T в (1.5.8) выбирается обычно в виде некоторого эффективного времени T эф установления переходного процесса в виде реакции y (t) системы управления с обратной связью на ступенчатое входное воздействие (функцию Хевисайда) x (t)= q (t), как показанное на рис. 1.5.2. Другой распространенной для переходных процессов в замкнутых системах управления оценкой качества является установившаяся ошибка e ¥ системы. Для идеальной (без помех) замкнутой системы автоматического регулирования, содержащей объект с передаточной функцией G и цепь обратной отрицательной связи с передаточной функцией R, ошибка равна
Следовательно, установившаяся ошибка для X (s) = 1/ s равна
Забегая вперед отметим, что для ПИД-регуляторов в отсутствии шумов теоретическое значение e ¥ ® 0 (см. стр. 42).
Рис. 1.5.2 1.6. Робастные системы управления. Рассмотренные выше методы анализа и синтеза систем автоматического управления предполагали, что модели объекта и регулятора известны, и они имеют постоянные параметры. Однако модели реальной физической системы (ТО, ТП) и самого регулятора всегда будут неопределенными (неточными) по следующим причинам: - неконтролируемое изменение параметров; - непредсказуемые внешние возмущения; - шумы датчиков; - динамические свойства, не учтенные в моделях; - не учтенные запаздывания по времени; - изменение положения рабочих точек системы. Рассмотрим влияние на системы управления лишь некоторых причин. Чувствительность систем управления к изменению параметров. Рассмотрим случай, когда за счет изменения параметров объекта управления его передаточная функция приняла значение G (s) + D G (s). Тогда приращение передаточной функции замкнутой системы в соответствии с (1.3.28) примет вид (G >>D G ®0)
Чувствительность системы определяется как отношение процентного изменения передаточной функции системы к процентному изменению передаточной функции объекта. Из (1.6.1) следует, что чувствительность системы равна
Отсюда видно, что чувствительность замкнутой системы можно сделать меньше, чем ее чувствительность в разомкнутом состоянии (Ч = 1) путем увеличения коэффициента усиления обратной связи (R). Возмущение и шумы датчиков систем управления. Возмущение – это нежелательный входной сигнал, который оказывает влияние на выходной сигнал системы. Одновременно внутри системы могут присутствовать шумы. На рис. 1.6.1 показана система регулирования, в которой присутствует как возмущение v (t), приложенное ко входу ТО, так и шум n (t) измерительного устройства (датчика).
Рис. 1.6.1 Если передаточная функция ТО – G ТО(s), передаточная функция датчика – G И(s), передаточная функция регулятора – G Р(s), а передаточная функция устройства сравнения – G УС(s), то к выходному сигналу y(t) системы добавляются сигналы, образы Лапласа которых имеют вид
где N (s) и V (s) – образы Лапласа шума датчика и возмущения. Для достаточно большого коэффициента усиления регулятора будет выполняться условие G УС(s) G Р(s) G ТО(s) G И(s) >> 1. Тогда,
Для сигнала ошибки будем иметь в соответствии с (1.5.9)
(1.6.5) Из (1.6.4) следует, что необходимо стремиться к увеличению передаточной функция датчика G И(s), что эквивалентно максимизации отношения сигнал/шум на его выходе. Одновременно необходимо обеспечить большое значение коэффициента усиления обратной связи, т.е. G Р(s) G И(s) >> 1, чтобы снизить влияние возмущения на выходной сигнал. Внимание! Следует помнить, что увеличение коэффициента усиления обратной связи может привести к нежелательному эффекту неустойчивости системы управления, или ухудшению ее качества. Поэтому при синтезе систем управления необходимо обеспечить следующие цели: 1. Передаточную функцию П (s) с широкой полосой D s пропускания и правильным воспроизведением входного эталонного сигнала x (t). 2. Контур обратной связи с большим усилением, чтобы минимизировать чувствительность Ч (s). 3. Большое усиление в контуре обратной связи за счет G Р(s) G И(s) т.е. регулятора и датчика. Для этих целей синтезируют, так называемые, робастные системы управления. Робастная система управления должна обладать требуемым качеством несмотря на существенную неопределенность характеристик объекта управления. Из рассмотренных в разделе 1.5 регуляторов лишь только ПИД-регулятор обладает свойствами, позволяющими настроить его на робастное управление. В силу (1.5.5) ПИД-регулятор имеет передаточную функцию G Р(s) = K 1 + K 2 / s + K 3 s, (1.6.6) где K 1 = k, K 2 = k / T И, K 3 = k T Д. Для применения ПИД-регулятора к конкретному объекту управления надо настроить три коэффициента K 1, K 2 и K 3. ПИД-регуляторы особенно полезны для уменьшений установившейся ошибки и улучшения вида переходной характеристики, когда объект управления может быть аппроксимирован моделью второго порядка. Так, например, для ступенчатого входного воздействия X (s) = 1/ s и N (s) = N 0/ s 2 при s ®0 (фликер-шума) из (1.6.5) и (1.6.6) получим
Переходные характеристики. Типичная переходная функция системы второго порядка изображена на рис. 1.6.8.
Рис. 1.6.8 Для описания данной функции используются следующие переходные характеристики: - время нарастания Tr – время, необходимое для изменения переходной функции от 10% до 90% от ее установившегося значения, как показано на рис. 1.6.8; - максимальное значение M переходной функции; - время Tp достижения максимума; - С – установившееся значение; - максимальное относительное перерегулирование (M – C)/ C; - время Ts установления – время, необходимое для того, чтобы выходной сигнал вошел в определенную зону, прилегающую к установившемуся значению, и далее оставался в пределах этой зоны. Ширину зоны 2d обычно принимают равной 10% или 4 % от установившегося значения C. У системы второго порядка переходная функция обычно входит в d = 2% зону за четыре постоянных времени t, т.е. Ts = = 4 t. Пример 1.6.1. Стандартная форма передаточной функции системы второго порядка имеет вид
где w – собственная частота колебаний при отсутствии затухания, z – безразмерный коэффициент затухания. Реакция системы (переходная функция) на единичное ступенчатое воздействие равна
Обратное преобразование Лапласа дает (см. 1.3.13) y (t) = 1 – (1/ b) exp(– t / t) sin(bw t + q), (1.6.10) где b = Используя результаты примера 1.6.1, можно показать, что для систем второго порядка важнейшие переходные характеристики определяются через физические параметры систем следующим образом
Частотные характеристики систем. Предположим, что на вход системы с передаточной функцией G (s) подан синусоидальный сигнал x (t) = A cos(w t). (1.6.12) Тогда
Это выражение можно разложить на простые дроби
где G* (s) является функцией G (s) и обуславливает переходные процессы в системе в отсутствии внешнего воздействия. Поэтому установившееся движение определяется только двумя первыми членами выражения (1.6.14). Это означает, что в установившемся режиме реакция системы на синусоидальное воздействие также будет синусоидой той же частоты, т.е. при s = jw Y (jw) = k 1 = Y (– jw) = k 2 = Функция G (jw) является комплексной и называется частотной характеристикой системы G (jw) = ê G (jw)½exp(jj). (1.6.16) В соответствии с обратным преобразованием Лапласа выражения (1.6.14) реакция системы в установившемся режиме будет равна Y (t) = k 1 exp(jw t) + k 2 exp(– jw t) = = (A /2) ê G (jw)½ exp(jj) exp(jw t) + + (A /2) ê G (– jw)½exp(– jj) exp(– jw t) = = (A /2) ê G (jw)½ {exp[ j (w t + j)] + exp[– j (w t + j)]} = = A ê G (jw)½cos(w t + j), поскольку ê G (– jw)½= ê G (jw)½. Вопросы для самопроверки к главе 1. 1. В чем смысл отрицательной обратной связи? Что такое система регулирования? 2. Чем отличается автоматическая система управления от автоматизированной? 3. Перечислите и объясните основные этапы синтеза систем управления. Какой основной принцип управления заложен в процесс синтеза? 4. Изложите алгоритм исследования динамики физической системы. 5. В чем заключается принцип подобия при моделировании физических систем? 6. Динамика каких систем описывается дифференциальными, а каких разностными уравнениями? Пр
|

 ,
, = (1.3.24)
= (1.3.24) .
.
 , (1.3.26)
, (1.3.26)


 . (1.3.28)
. (1.3.28) . (1.3.29)
. (1.3.29)
 Здесь u 1 и u 2 – входные переменные, а x 1 и x 2 – выходные. Сигнальный граф, соответствующий уравнениям (1.4.1), изображен на рис. 1.4.2.
Здесь u 1 и u 2 – входные переменные, а x 1 и x 2 – выходные. Сигнальный граф, соответствующий уравнениям (1.4.1), изображен на рис. 1.4.2. , (1.4.3)
, (1.4.3) ,
,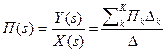 , (1.4.4)
, (1.4.4)
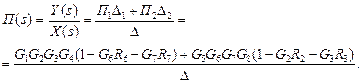
 Пример 1.4.2. Сигнальный граф сложной системы с несколькими контурами и прямыми путями изображен на рис. 1.4.4.
Пример 1.4.2. Сигнальный граф сложной системы с несколькими контурами и прямыми путями изображен на рис. 1.4.4.

 ,
, .
. , или (1.5.2)
, или (1.5.2) .
. или (1.5.3)
или (1.5.3) .
. или (1.5.4)
или (1.5.4) .
. или (1.5.5)
или (1.5.5) .
. (1.5.6)
(1.5.6) – половина зоны неоднозначности регулятора; sign означает знак выражения в скобках.
– половина зоны неоднозначности регулятора; sign означает знак выражения в скобках. (1.5.7)
(1.5.7) На рис. I.5.1 показаны графики координат e и u для различных идеальных законов регулирования при образовании в момент t = 0 скачкообразного отклонения регулируемой величины из-за изменения нагрузки.
На рис. I.5.1 показаны графики координат e и u для различных идеальных законов регулирования при образовании в момент t = 0 скачкообразного отклонения регулируемой величины из-за изменения нагрузки.
 Рис. 1.5.1
Рис. 1.5.1 ). Площадь, ограниченная прямой e = const и концевыми ординатами t = 0 и t = var, больше, естественно, площади под наклонной u (t) с теми же концевыми ординатами для моментов времени до пересечения прямых e (t) и u (t). Но эти площади пропорциональны интегралам
). Площадь, ограниченная прямой e = const и концевыми ординатами t = 0 и t = var, больше, естественно, площади под наклонной u (t) с теми же концевыми ординатами для моментов времени до пересечения прямых e (t) и u (t). Но эти площади пропорциональны интегралам  и
и  , т.е. количествам энергии или вещества, аккумулированным в регулируемом объекте и удаленным из него. Поэтому при компенсации регулятором разбаланса потоков из-за возмущения при нагрузке, аккумулированное в объекте количество энергии или вещества ниже заданного (например, действительное теплосодержание ниже предписанного, определяемого по номинальному значению регулируемой температуры). Поэтому происходит дальнейшее возрастание выходной координаты регулятора и неизбежно наступает перерегулирование с последующим колебательным процессом изменения регулируемого параметра.
, т.е. количествам энергии или вещества, аккумулированным в регулируемом объекте и удаленным из него. Поэтому при компенсации регулятором разбаланса потоков из-за возмущения при нагрузке, аккумулированное в объекте количество энергии или вещества ниже заданного (например, действительное теплосодержание ниже предписанного, определяемого по номинальному значению регулируемой температуры). Поэтому происходит дальнейшее возрастание выходной координаты регулятора и неизбежно наступает перерегулирование с последующим колебательным процессом изменения регулируемого параметра. . (1.5.8)
. (1.5.8) . (1.5.9)
. (1.5.9) . (1.5.10)
. (1.5.10)
 . (1.6.1)
. (1.6.1) . (1.6.2)
. (1.6.2)
 , (1.6.3)
, (1.6.3) ,
, , (1.6.4)
, (1.6.4) , G УС @ 1.
, G УС @ 1. .
. , т.е. e ¥ ® 0 для N 0 ® 0. (1.6.7)
, т.е. e ¥ ® 0 для N 0 ® 0. (1.6.7)
 , (1.6.8)
, (1.6.8) . (1.6.9)
. (1.6.9) , q = arctg(b / z), t = 1/ zw – постоянная времени.
, q = arctg(b / z), t = 1/ zw – постоянная времени. ,
,  . (1.6.11)
. (1.6.11) и
и . (1.6.13)
. (1.6.13) , (1.6.14)
, (1.6.14) , (1.6.15)
, (1.6.15) .
.


