Выбор общей модели расчета параметров состояния
При выборе модели расчета параметров состояния системы используется одна из известных общих моделей: управления запасами, общая линейная модель распределения, модель задачи о назначениях, модель задачи о размещениях (транспортная задача), динамического программирования,"продавца газет", "дерево решений".
Для управления запасами наиболее простая общая модель расчета параметра состояния системы у, представляемого в виде издержек, зависящих от: · расходов, связанных с размещением заказа и поставок партии - к; · издержек на содержание единицы продукции в единицу времени - S; · спроса - V; · размера партии поставок q, имеет вид y = L = где L - издержки на содержание запаса в единицу времени. Эта модель справедлива при условиях, что: - уровень запаса снижается равномерно в соответствии с равномерно поступающими требованиями V (спросом), который может быть определен как: V = где Q - общий объем поставок; Т - время обеспечения запасом в объеме Q. - заказ на поставку партии подается, когда запас исчерпан и выполняется мгновенно. - расходы, связанные с размещением заказа и поставок партии не за Если в качестве параметра процесса взять время t, то издержки от начала процесса (момента to=0 поставки первой партии q) будут рассчитываться по формуле: L(t) = ( Эта модель может использоваться как для определения «фактического» состояния по истечении некоторого интервала времени, меньшего или равного Т, так и прогнозирования издержек на поддержание запаса в оставшейся до момента Т временной отрезок. Так, положив t равным Т, получим прогноз общих издержек при работе с принятой партией q, вычисляемых по формуле: L(t) = Подставляя вместо Vего значение V =
L(t) = kn + S где п = Для прогнозирования издержек в произвольный момент времени t1 (0< t1 < Т) определим оставшийся отрезок времени (Т – t1) и объем поставки Q(T-t1). Тогда расчет параметра состояния L (издержек) в зависимости от неуправляемых (постоянных) параметров k, S, V и управляемой переменной q в любой момент времени t1 будет осуществляться по формуле: L(k, S, Q(t), T(t), q) =
В распределительных задачах модель определения состояния связывает параметры состояния - величину получаемой прибыли, убытка, времени выполнения работ, издержек материалов, трудовых ресурсов и т.д. - со значениями распределяемых величин через постоянные параметры, характеризующие "вклад" каждой распределяемой величины в данную характеристику состояния. Например, в цехе имеется три группы взаимозаменяемого оборудования с мощностями M1, M2, M3 норма-часов в месяц. Цеху необходимо выпустить 5 видов продукции в объемах П1, П2, П3, П4, П5. Время изготовления единицы каждого вида продукции j на i - оборудовании составляет tij. Например, время изготовления единицы продукции П2 на первом виде оборудования t12 = 0,6 часа. Известны денежные затраты на изготовление единицы продукции j на каждом i-виде оборудования. Например, затраты на изготовление единицы П3 на втором виде оборудования составляют Z 23 = 40 рублей. Известна отпускная цена C1 каждого вида продукции C1, C2, С3, C4, C5. Процесс распределения состоит в размещении заказов по видам оборудования, т.е. определении доли xij объема продукции Пj на каждом виде оборудования i. Количественная оценка состояния в рассматриваемой задаче определяется зависимостью от выбора значений управляемых переменных хij и включает три характеристики: 1. Состояние по загрузке мощностей y1. 2. Состояние по выполнению объема у2. 3. Состояние по прибыли у3.
Состояние y1 включает три компонента у11, у12, у13, определяющие загрузку групп оборудования:
y11 = t11 x11 + t12x12 + t13x13 + t14x14 + t15x15 y12 = t21x11 + t22x22 + t23x23 + t24x24 + t25x25 y13 = t31 x31 + t32x32 + t33x33 + t34x34 + t35x35
Состояние у2 включает пять компонентов y21……y25, определяющих выполнение заданий по изделиям при их изготовлении на различных
y21 = x11 + x21 + x31 y22 = x11 + x22 + x32 ……………………….. y25 = x15 + x25+ x35
Состояние уз характеризуется числовым значением прибыли, определяемой как сумма произведений прибыли от одной единицы продукции на ее количество хij: y3 =
или y3 = (C1 – Z11) xn + (C2 – Z12) x12 + …..+ (C5 – Z15) x15 + (C1 – Z21) x21 + ……..+ (C5 – Z25) x25 + (C5 – Z31) x31 + …. + (C5 – Z35) x35 Параметром процесса в распределительных задачах являются моменты поступления входных данных. Расчет параметров состояния в модели динамического программирования производится путем разбивки процесса принятия решения на ряд однотипных этапов, каждый из которых планируется отдельно, но с учетом состояния системы на начало этапа и последствий принятого решения в будущем. Последний этап изучается отдельно и планируется наилучшим образом. Состояние системы на каждом этапе определяется набором характеристик x1, x2, хn. Дальнейшее изменение ее состояния зависит только от данного состояния и не зависит от того, каким путем система пришла в него. На каждом шаге выбирается одно решение, под действием которого система переходит из предыдущего состояния в новое, причем это решение связано с выигрышем или потерей, которые зависят от состояния на начало этапа и принятого решения. Программирование разворачивается от конца к началу. Оно осуществляется на основе предложений об ожидаемых исходах предшествующего, еще неисследованного состояния. Находится наилучшее управление, зависящее от возможных исходах (характеристик состояния) предыдущего этапа. Завершив анализ конечного этапа, рассматривают аналогичную задачу для предпоследнего этапа, требуя, чтобы функция цели достигла экстремального значения на двух последних этапах вместе. Проделав такой процесс определения наилучших (условно-оптимальных) управлений для каждого шага от конца к началу, а затем от начала к концу находят оптимальное управление (стратегию) для каждого шага с точки зрения всего процесса. Рассмотрим простейший пример применения модели расчета параметров состояния методом динамического программирования. Пусть задана транспортная железнодорожная сеть (рис. 8), на которой указаны пункт отправления А, пункт назначения В и расстояние между пунктами. Требуется составить маршрут из пункта А в пункт В минимальной длины.
Рис. 8. Транспортная сеть.
Для использования модели динамического программирования разобьем расстояние между А и В на этапы как показано на рис. 9. Оценим отрезки, на которые делят участки сети этапы 2-2 и 3-3. Например, этап 2-2 делит участок длиной 5 на два участка длиной 2,5. Последний этап 2-2 характеризуется состоянием, включающем три точки (D1, D2 и D3). Выбор кратчайшего пути начнем с конца. Определим точку состояния, соответствующую минимальному пути до точки В. Для точки D1 min (10; 8+4; 8+3+5) = 10; для D2 min (5+4; 5+3+5) = 9; для D3 min (2,5+3+4; 2,5+5) - 7,5. (Эти расстояния указаны в скобках). Далее рассматриваем состояние второго этапа, включающие точки C1, С2, С3. Кратчайшее расстояние от этих точек до пункта В показаны в скобках. Наконец находим длину минимального пути, ведущего из А в В. Это расстояние равно 23 единицам. Затем проходим этапы в обратном порядке и находим кратчайший путь. Он выделен жирной линией.
Рис. 9. Этапы решения задачи....
Эта задача находит применение для определения значений Cij -удельных затрат на перевозку (тарифов) - в транспортной задаче. Для того чтобы использовать модель "дерево решений" необходимо отразить процесс принятия решения в виде перехода системы из одного состояния в другое. Он включает последовательность состояний и связей между ними и изображается в виде графа, моделирующего варианты возможного перехода системы из исходного события в завершающее. Узлы отражают состояния, в которых возникает необходимость выбора (принятия решения), а ветви - события, которые могут иметь место после принятия решения. При этом существует два вида решений, выбираемых ними и осуществляемых "природой" и "рынком". Такой подход можно использовать для решения задач, связанных с неопределенностью развития систем, перехода из одного состояния в другое в условиях неопределенности. Например, пусть модель, представленная на рис. 10, отражает фрагмент модели организации студентами мероприятия "Элегант - шоу".
а) -200р
Рис. 10. Граф состояний
Блок 1 отражает исходное состояние, ветвь А - заключение договора с- ДК "Интеграл", ветвь В - отказ от договора. В случае заключения договора (ветвь А) вероятность "решения" природой того, что будет найдено необходимое количество команд (ветвь N) равная 0,3, а не найдено (ветвь М) равна 0,7. В блоках 3 и 4 принимаются решения: проводить рекламную компанию (ветвь С) или не проводить (ветвь D). В случае проведения компании природа может обеспечить осуществление "Элегант - шоу" и обеспечить получение выручки 5 тыс. рублей или не проведение и убыток в 200 рублей. Для определения "иены" узлов 5, 6, 3 и 4 используются условные вероятности, а для нахождения оптимальной стратегии - метод динамического программирования.
|

 +
+  ,
, ,
, + s
+ s 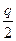 T,
T, есть количество произведенных циклов поставки.
есть количество произведенных циклов поставки. + S
+ S  ,
,





