Формулировка математической задачи оптимизации
Объединяя результаты предыдущих этапов построения математической модели, ее можно записать в виде математической задачи оптимизации. Если известна целевая функция Z(x), то для записи задачи оптимизации в общем виде используется символика: Z(x) → min (max) = fG x € U, где U - допустимое множество, заданное ограничениями на управляемые переменными. Для управления запасами математическая задача оптимизации запишется как:
L = 0 < q ≤ qmax, где qmax - есть предельно возможная, например, из-за грузоподъемности транспорта, денежных ресурсов или других причин партия поставки. Для управления распределением в ситуации, приведенной в п. 8.4 и 8.5, можно рассмотреть несколько вариантов. 1. Оптимизация прибыли: Z1 = y3 = при 0 < y11 ≤ M1 0 < y12 ≤ M2 0 < y13 ≤ M3, y21 = П1, y22= П2, y23 = П3, y24 = П4, y25 = П5
2. Минимизация денежных затрат Z2 = при тех же ограничениях, что в п. 1. 3. Минимизация затрат времени: z3 = при ограничениях y21 = П1, y22 = П2, y23 = П3, y24 = П4, y25 = П5, Z = y3 =
где Zmin - минимально допустимая величина прибыли. Формулировка задачи оптимизации в моделях динамического программирования (с закрепленными концами) состоит в определении начального и конечного состояний, этапов перехода, количественных характеристик состояния каждого этапа и формулировке критерия принятия решения на каждом этапе.
8.7. Построение модуля выработки оптимальных (формальных) решений В п. 4.3 было дано определение модуля. Модуль выработки решений в соответствии с математической задачей оптимизации по входам; постоянным параметрам и управляемым переменным. Полученные на выходе оптимальные решения являются теми значениями управляемых переменных, которые доставляют экстремальное значение целевой функции, т.е. являются наилучшим путем достижения цели и поэтому играют роль управляющих воздействий (управлений) на управляемый процесс. Представим процесс выработки решений в виде формальной модели процесса. Тогда, для того, чтобы построить модель выработки решений необходимо: Определить входы х+, выходы х-, постоянные а и переменные факторы х, влияющие на выход х-. Определить параметры состояния у Выбрать модель расчета параметров состояния у по входам х+, постоянным параметрам а, управляемым переменным х (правило S). Выбрать числовой критерий оптимизации Z. Сформулировать математическую модель оптимизации. Реализовать правило формирования оптимального выхода в соответствии с математической моделью оптимизации (правило V, V или V и V) х-= V(x+,a,t,y) х-= V(x+,a,t) На выходе модуля получаем выходные характеристики х- в виде на Такой модуль может быть условно назван "решателем", поскольку он вырабатывает управления в соответствии с законом управления, задаваемым правилами S, V или V. Его схематично можно представить как показано на рис. 11.
Рис. 11. Схема модуля "Решатель"
На рис. 11 буквой G обозначена цель, в соответствии с которой выствий, позволяющих получить экстремальное числовое значение критерия, характеризующего достижение цели. Рассмотрим построение модуля формальной выработки решений ("'решателя") на примере процесса управления запасами. Входы: x+1 - количество Q1 ресурса i х+2 - время Т, на которое требуется обеспечение ресурсом i Постоянные параметры: a1 = k - издержки на размещение и поставку партии а2= S - издержки на содержание запаса аз = V - спрос Переменная(управляемая)величина: q - партия поставки ресурса Параметр состояния издержки на обеспечение запасом: y = L Модель расчета параметра состояния в единицу времени:
y = L = Числовой критерий оптимизации
Z = L =
Математическая модель оптимизации: L = 0 < q ≤ qmax Формирование выхода: x-1 = V (k,V,S,q) Правило V соответствует оператору отысканию оптимального значения q=x-1 обращающего в нуль производную числового критерия оптимизации L по q, т.е
И нахождения оптимального значения цикла поставки t- = Правило V формирует выход х-3, определяющий значение затрат на время t, т.е. х-3 = L t.
Теперь "решатель" можно изобразить схематично как; показано на
Рис. 12. Модуль выработки формальных решений в процессе управления запасами Аналогично можно представить "решатель" для задач распределения, а также динамического программирования (для одного этапа). В курсовом проекте в модуле "решатель" символы должны быть отображены конкретными числами, характеризующими управляемый процесс в соответствии с информационным обеспечением (см. п.9)
8.8. Построение модели замкнутой (динамической) системы управления. 8.8.1. Структура цикла непрерывного управления Модель замкнутой системы управления строится по принципу управления процессом для получения некоторого конечного результата (выхода). Она включает управляемый процесс, фактический выход и управляющую систему, обеспечивающую достижение конечного результата. Эти блоки образуют контур регулирования с отрицательной обратной связью. Представим его в виде блок-схемы:
Рис. 13. Структура замкнутой системы управления
Сенсором является некоторое устройство, механизм, который считывает значение контролируемой переменной. Задатчик цели задает стандарт - эталон с которым будет сравниваться полученный результат. Это сравнение осуществляется блоком, называемым дискриминатором или компоратором. Различия между действительными и фактическими значениями переменных передаются в блок формирования решения, который определяет, какое именно действие (управление) должно быть выполнено исполнительным органом-эффектором. ■ Блок "формирования решения для рассматриваемого объекта был сформулирован в соответствии с п. 8.4. При выполнении настоящего раздела следует иметь ввиду, что замкнутая система управления является динамической системой и предназначена для долговременного управления процессом, протекающим во времени и в условиях воздействия окружающей Среды. В предыдущих разделах процессы управления запасами, распределением, процесс принятия решения рассматривались как операция принятия решения в фиксированный момент времени на какой-то промежуток времени. В общем случае необходимо рассмотреть непрерывное функционирование объекта во внешней среде. Моделью, способной отобразить поведение управляемой системы к требованиям (целям) и возмущающим воздействием внешней Среды, является приведенная на рис. 1,3 кибернетическая модель управления. Она позволяет получать непрерывно конечный результат, соответствующий поставленной цели и ограничениям и поэтому, с точки зрения организационных систем, называется управлением по конечному результату. Фактически достигаемый конечный результат измеряется входным анализатором. Он с помощью сенсора (датчика) измеряет фактическое значение результата, а дискриминатор сопоставляет его с желаемым (эталоном), в результате чего становиться ясно: требуется ли принимать решение и воздействовать (корректировать) управляемую систему на следующем цикле или нет. Рассмотрим построение модели системы управления на примере управления запасами.
8.8.2. Динамическая модель управления запасами В начале рассмотрим управляемый процесс во времени. Он состоит в пополнении запаса элементов на некотором складе, причем потребление элементов может случайным образом колебаться. Поэтому вместо константы v, характеризующей расход в простейшей модели, он является некоторой случайном величиной р (t - to) за период времени между текущим моментом t и моментом предыдущей поставки партии to. Фактическое состояние запаса на складе у (t) в текущий момент времени t определяется выражением: y(t) = y(to)+Zqi(t-to)-Zpi(t-to), где у (to) - запас элементов в момент времени to. ∑ qi (t - to) - суммарное поступление элементов с момента to. ∑ pi (t - to) - суммарный расход элементов с момента to Тогда модель склада можно изобразить схемой в виде модели:
Рис. 14. Модуль формирования состояния склада
Задатчик цели формирует две цели. Первая - непрерывное обеспечение ресурсом потребителя. Мерой оценки ее достижения служит эталон в виде неснижаемой величины запаса в количестве "∆". Вторая минимизация издержек на поддержание и хранение запаса, т.е. требование L —> min. Схема модели замкнутой (динамической) системы управления процессом показана на рис. 14. Значение эталона “∆” поступает в дискриминатор, значение цели - в блок принятия решения. Сенсор учитывает фактическое количество элементов на складе путем их визуального наблюдения и счета. Полученное количество у (t) отражает фактическое состояние y(t) с некоторой погрешностью, определяемой точностью учета и временным интервалом. Полученные данные у (t) сравниваются со значением эталона "∆". Если у (t)>∆, то уровень запаса допустимый и необходимости пополнения запаса и принятия решения о размере партии поставки нет. Если y'(t)<∆, то уровень запаса снизился до эталона или ниже и требуется определить размер заказа. Поэтому с дискриминатора передается управление блоку принятия решения, который "обеспечивается" информацией о значениях Q и Т, рассчитанных на момент времени t: Q(t) = Q - ∑ q-1 T(t) = T – (t-t0)
Полученное в блоке принятия решений (в момент снижения запаса до уровня ∆) управление передается в исполнительную систему для организации поставки партии элементов в количестве q". После поставки партии значения Q и Т корректируются. Заметим, что поскольку расход элементов случайный, то цикл поставки будет определяться временем снижения уровня запаса до установленной величины неснижаемости запаса. Описанный процесс отображается в виде блок-схемы модели замкну
Рис. 15. Схема динамической модели управления запасами
Обозначения: → информация => материальные элементы
9. ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
Для того, чтобы модель была пригодной для практического применения ее необходимо "обеспечить" информацией о текущих значениях, входящих в нее величин параметров. С этой целью в общем случае необходимо: · определить подразделения, в которых формируется или поступает · определить первичные документы, из которых берется информация; · определить процедуру обработки информации для вычисления значений параметров; · установить каналы передачи информации из подразделений в систему управления. Например, в системе управления распределением электроэнергии на подстанции, модель определения состояния по потерям мощности содержит величины k, Ini, T, а также ограничения по напряжению и сечению проводов Un i max И Sn i max. Величина "к" - стоимость кВт ч электроэнергии одинакова для всех энергосистем. Расстояние до i-гo объекта 1ni,а (n= 1,5; i = 1,4), где n - номер фидера (схемы снабжения объектов электроэнергии), i - номер объекта внутри фидера, определяется по схемам, приведенным в приложении. Величина Т принимается равной месяцу - 720 час/м. Величины Ini,Unimax и Snimax зависят от конкретных условий передачи электроэнергии и представлены в таблице 2. Таблица 2
При управлении процессом оптимального распределения активов банка модель определения состояния дохода включает затраты на привлечение j-гo вида пассивов в конкретный i-й вид актива (сij), суммарные данные о вкладах граждан, депозитов предприятий, средств на расчетных счетах клиентов, собственных векселях. Схема информационного обеспечения подразделения "Управление анализа и планирования", которое решает названную нише задачу покапана па рис. 16.
Рис. 16. Схема информационного обеспечения модели управления использованием пассивов.
В процессах, cвязанных со случайностью, необходимо использовать статистические данные о значениях случайной переменной. Например, пусть статистика о спросе (продаже) хлеба в торговой фирме за 12 недель по дням недели имеет вид, приведенный в табл.3. Таблица 3.
Для оценки частоты появления того или иного значения случайной величины (объема продаж) в день недели, например, понедельник, определим разброс случайной величины. Он составляет (5,1-7,7). Разобьем весь интервал от 5 до 8, например, на 6 интервалов: 5,0-5,5; 5,51-6,0; 6,01-6,5; 6,51-7,0; 7,01-7,5; 7,51-8,0. Из таблицы видно, что в первый интервал попало 3 значения, во второй - 6, в третий - 1, в шестой - 1. Если значение случайной величины заменить ее средним значением в интервале, то получим 5,25; 5,7; 6,25; 6,75; 7,25; 7,75. Тогда частота (вероятность) появления этих значений в понедельник составит: р(5,25) = 3/11= 0,27 р(5,75) = 6/11= 0,55 Р(6,25)= 1/11 =0,09 р(7,75)= 1/11 =0,09
Эти оценки могут быть использованы для определения математического ожидания случайной величины в модели. В информационном обеспечении следует предусмотреть сбор, обработку, передачу информации в управляющую систему (кто формирует, где и как обрабатывается, в какой блок модели передается, когда корректируется). В моделях управления запасами содержатся величины "к" и "S", со- ответствующие расходам на размещение и поставку заказа и на содержание единицы запаса в единицу времени. Стоимость размещения заказа к устанавливается по данным отдела снабжения и бухгалтерского учета. В информационном обеспечении необходимо показать (и приложить) соответствующие документы и процедуру определения величины к. Издержки содержания единицы продукции в единицу вре'мени S зависят от:
Необходимо отразить, как формируются эти данные и определяется значение S для использования в модели.
10. ОПРОБОВАНИЕ МОДЕЛИ. ЗАКЛЮЧЕНИЕ Полученные при разработке информационного обеспечения конкретные числовые значения и входные данные необходимо "ввести" в модель "решателя" и провести пробное решение для получения значения оптимального управления на одном цикле управления. Полученные результаты сопоставляются с результатами функционирования реально существующего объекта. Например, в задачах управления запасами можно использовать данные об отчетности движения конкретного вида материала (товара) по форме, приведенной на рис.18.
Рис. 18. Форма статистических данных
Фактический объем партии поставки определяется по формуле: q = а фактические издержки по формуле: L = kn + которые можно сравнить с полученными в проекте. В приведенном выше примере управления распределением электроэнергии на подстанции в результате подстановки в модуль оптимизации реальных данных и ограничений получены издержки 830,54 руб., в то время как существующие убытки составляют 2580 руб. В заключении пояснительной записки приводятся выводы, вытекающие из всей работы, неучтенные факторы, которые следовало бы учесть при дальнейшем исследовании и связанные с этим трудности, рекомендации по использованию спроектированной модели системы управления. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Р. Акоф, М. Сасиени. Основы исследования операций. Мб Мир, 1971. 2. ВА. Сакович. Исследование операций (детерминированные ме 3. У. Черчмен, Р. Акоф, Л А. Арноф. Введение в исследование опера 4. Е.С. Вентцель. Исследование операций. Задачи, принципы, мето 5. В.В. Лесин, Ю.П. Лисовец. Основы методов оптимизации. -М: Из 6. Воронов АА. Исследование операций и управление. -М: Наука, 7. В А. Губанов, В.В. Захаров, А.И. Коваленко. Введение в системный 9. Букан Д., Кенигсберг Э. Научное управление запасами. -М, 1967. Наговицына Л.П. Как управлять товарными запасами? -М, 1989. Спец. литература по выбранному объекту.
|

 +
+  → min
→ min → max
→ max → min
→ min → min
→ min
 = 0
= 0







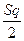 T,
T,


